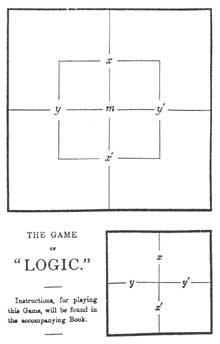
Diagrama logikoak (I)

Matematikaren historian zehar irudiak oso baliagarriak suertatu zaizkie matematikariei. Zenbakietatik hasita, zuzenak, planoak, espazioa, elipseak, zirkunferentziak, konoak, paraboloideak, sinu eta cosinu funtzioak, esponentzialak, bi, hiru eta lau aldagaiko funtzioak, funtzio konplexuak eta matematikaren munduan existitzen diren mila gauza gehiago irudikatu dira. Are gehiago esango genuke: gauzak irudikatzeko ezezik zenbait propietate, lema eta teorema frogatzeko ere erabili dira.

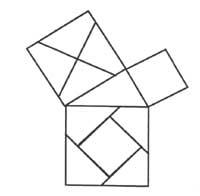
Adibide gisa, zenbait kasu aipatuko genuke: Arkimedes-en heriotzari buruz dugun mitoa, kondaira edo historia. K.a. 212. urtean, soldadu eromatarrek Siracusa hiria armaz hartu zutenean, Arkimedes frogapen geometriko batean sor zegoela soldadu batek hil zuen ezpataz. (Garai hartan irudiak harean egiten zirela gogoan izan behar da). Baina horren tragikoa izan gabe ere, hortxe dugu Pitagoras-en teoremaren frogapena irudien bidez (1. irudia). Azkenik M. Willians maisuaren artikulua dugu, zeinetan tangram-aren laguntzaz Euklides-en zenbait frogapen matematiko agertzen bait da.

Baina ildo honetan matematikariak urrunago joan dira, eta ez dira geratu orain hain ezagunak ditugun kontzeptu hauen irudikapenetan. Beraien ausardia urrunago joan da eta lengoaia, ideia, arrazonamendua bera, irudikatzera iritsi dira. Logika dela medio, matematika eta filosofia elkartzen dira. Gu logikaren irudikapenaz mintzatuko gatzaizkizu artikulu honetan.

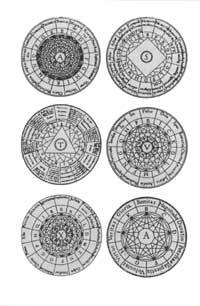
Arrazonamenduak irudikatzen aitzindaritako bat Ramon Llull kataluniarra dugu. Bere Ars Magna izeneko maisulanean zirkulu zentrukidezko sistemen bidez edozein gai azaldu nahi izan zuen. Besteak beste (2. irudia), Jainkoa (A,A) eta arimaren (S) nolakotasuna, gauzen arteko erlazioa (T), zazpi bertute eta zazpi bekatu buruak (V) edo gezurra eta egia (X). Llull-ek zirkuluak higituz lortzen zituen konbinazio posible guztiak.

Aparteko aipamen hau egin ondoren, eta beste aitzindari batzuk ahaztuz, logikaren analisiaren historian erabili zen lehenengo sistema deskribatzera goaz. Hau Venn-en diagramena besterik ez da. Venn-en diagramak, matematika modernoaren barruan oinarrizko gai dugun multzo-teorian erabili dira. Horretaz gain Aristoteles greziarrarengandik heredatutako logika klasikoa eta bertan silogismo kontzeptuak zituen arazoak konpontzeko balio izan du.

Dudarik gabe Boole-ren klase-algebraren definizioaren agerpenak eragin handia izan zuen Venn-en diagramek lortutako arrakastan.

Eman ditzagun, hasteko, diagramekin ondo ibili ahal izateko oinarrizko arauak:

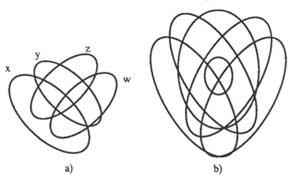
– Zirkulu bakoitzak klase bat irudikatuko du; zirkuluaren barruan dauden puntuak klasekak izango dira eta kanpokoak ez-klasekoak izango dira. Klasea S bada ez-S adierazteko &S idatziko dugu. Hirugarren irudian hiru klaseko diagrama ikusten da.

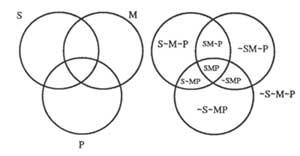
– Klase batean elementurik ez dagoela adierazteko, ilundu egingo dugu. Elementuren bat dagoela adierazteko X idatziko dugu. Elementuak ondoz-ondoko bi eskualdetan egon balitezke, X mugan idatziko dugu.

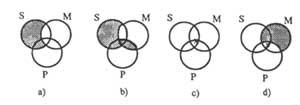
Laugarren irudian ikus daitezke ondoko premisen diagramak

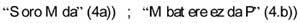
4b) diagrama ikusita, zera ondorioztatzen da: “S bat ere ez da P”.

“Zenbait S M da” (4c)) (X mugan dago, elementuak batean, bestean edo bietan non dauden ez dakigulako).

Bigarren premisa “M oro P da” balitz, X erdikoan idatzi beharko genuke: 4d).

Hiru baino gai gehiago agertzen denean, konplikatu egiten da. Zirkuluen ordez elipseak erabili behar dira, 5 a), eta batzuetan irudi ez-konexuak 5b).

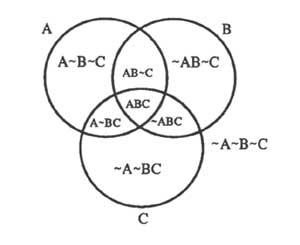
Klase-kalkuluaren interpretazio bezala sortutako proposamendu-kalkuluan ere erabil daiteke. Horretarako emandako arauak aldatu egin behar dira eta beste interpretazio bat eman behar zaie. Orain zirkuluek proposamenak adierazten dituzte. Hauek egiazkoak ala faltsuak izan litezke. Lehen elementurik gabeko eskualdeak ilundu egiten genituen. Orain ere ilunduko dira, egibalioen konbinazio ezinezkoak adierazteko. Seigarren irudian lau zirkulu agertzen dira: handiak (A, B eta C) proposamenduei dagozkienak eta txikia (ez A ez B ez C, &A&B&C) A, B eta C proposamenduekiko kanpo-aldea adierazteko eta ilunketa errazteko.

7. irudian adibide batzuk ikus daitezke:

7a) “A egiazkoa da”; 7b) “A faltsua da” (edo “&A egiazkoa da”).

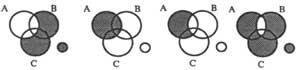
“Baldin A egiazkoa bada B egiazkoa da” baldintzazko diagrama, A … B idatziko dugu. Erlazio honi dagokion egitaula EE, EF, FE eta FF da (Egiazkoa, Faltsua), hauetatik EF-k bakarrik ez du balio. Beraz A&B (A, ez B) daukaten eskualdeak ilundu behar dira 7 c) diagraman ikusten den bezala, hau da, hain zuzen ere “A oro B da” proposamenduari dagokion diagrama. Aurreko proposamenduari “A egiazkoa da” proposamendua gehitzen badiogu, hots &A ilundu, 7d) irudiko diagrama lortuko dugu eta ondorio bezala “B egiazkoa da” ateratzen dugu.

7b) irudian ikus daitekeenez A faltsua izateak ez du B-k faltsua edo egiazkoa izan behar duela inplikatzen; bata ala bestea izan daiteke. Aldiz 7d) irudian A egiazkoa izateak B-k alabeharrez egiazkoa izan behar duela ikusten da.

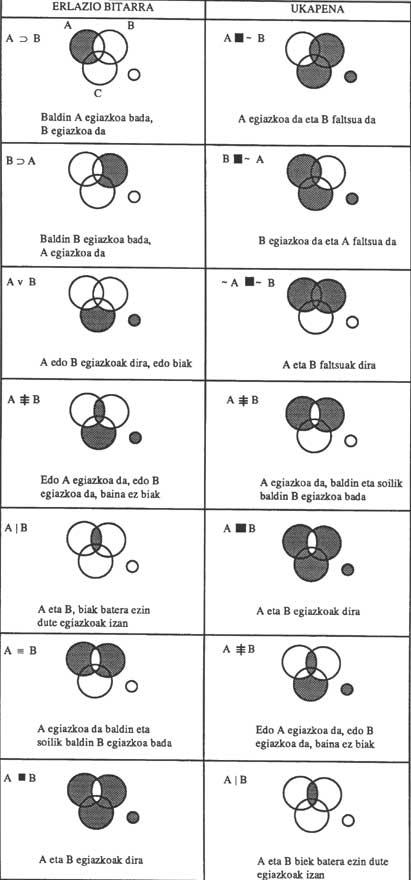
Zortzigarren irudian A eta B gaien arteko erlazio bitar guztien, eta hauen ukapenen, diagramak ikus daitezke. C hirugarren gaia ere azaltzen bada, diagrama hiru gaietara oso erraz heda daitekeelako da. Lehenago idazkera azalduko dugu:

Oraingoz hemen utziko dugu Diagrama Logikoen deskribapena. Hurrengo alean, Elhuyar. Zientzia eta Teknika 26. alean (Irailekoan) artikuluaren bigarren eta azken zatia argitaratzeko asmotan gara eta horrela gaiaren deskribapen osoa amaitutzat emango dugu.