"Principia" 300 anos (2) Isaac Newton, creador do cálculo

1987/04/01 Duoandikoetxea Zuazo, Javier - EHUko matematika irakaslea Iturria: Elhuyar aldizkaria

• Fisika

Camiñando

A Matemática grega, baseada en gran medida na Xeometría, parece normal que se queira calcular a superficie das figuras planas e o volume dos sólidos. Do mesmo xeito, ao dar os primeiros pasos da Física mostraron interese por conseguir un centro de gravidade. A maior parte destes problemas débense a Arquímedes, un servente (a. C.). III. No século XIX): superficies de elipses e segmentos parabólicos, volume de moitos sólidos de revolución (esfera, elipsoide, segmento de paraboloides, etc.) e o centro de gravidade da maioría, por exemplo.

Pero Arquímedes non tiña a formulación fácil que ofrece o Cálculo actual (a integral dunha soa función dá lugar a varias resulsiones de Arquímedes) e cada problema era novo paira el. Paira a obtención dos resultados valeuse da súa intuición xeométrica, descompondo a miúdo a imaxe en fragmentos moi pequenos e aproximando estes por figuras coñecidas (triángulos, cadrados, cilindros). Posteriormente, paira xustificalo, utilizaba o "método exhacutivo" adoptado por Eudel.

Pronto as Matemáticas (polo menos as relacionadas co cálculo) quedaron durmidas e con ela os traballos de Arquímedes. Os árabes trouxeron estas obras ao oeste de Europa, onde foi o XVI. No século XX retomaron o seu estudo. XVII. Pódese dicir que a principios do século XX entendíanse as obras de Arquímedes, polo menos o suficiente paira dar novos froitos. Nese cincuenta anos até chegar a Newton acumuláronse nomes e rescatados: Kepler, Cavalieri, Torricelli, Roberval, Descartes, Fermat, Pascal, Wallis, Barrow, etc.

Da man de Descartes, a Xeometría Analítica tivo una gran influencia no Cálculo, xa que a expresión algebraica das curvas provocou una nova e áxil formulación de problemas. Un paso importante foi o da clasificación de problemas, con dous grandes grupos: os problemas de tangentes e os problemas de superficies, que os reciben dos modelos principais. Os problemas do primeiro grupo (rectificar una curva nun punto ou calcular os máximos e mínimos) eran practicamente novos, xa que nas Matemáticas antigas non aparecen e resólvense mediante a derivada. Os do segundo grupo, con todo, son formulados por Arquímedes e hoxe asociámolos á integración.

Entre os matemáticos arriba mencionados, Fermat foi o máis avanzado na resolución destes problemas. Paira o cálculo de máximos e mínimos, por exemplo, deu o seguinte método: Achar o valor A para o que [F(A + E) - F (A)] / E = 0, facendo E = 0 (una vez obtido o cociente). Aínda que pareza un derivado, aquí non hai límite, xa que Fermat faio paira polinomios, onde o cociente é sempre exacto. En integración, hoxe

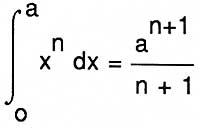
coñecía o equivalente xeométrico da fórmula, algo demostrado en Cavalieri, Pascal ou Roberval.

E chegou Newton

O mozo Newton coñeceu e pronto dominou as técnicas dos libros de Matemáticas lendo o seu propio libro. Esta formación autodidáctica non é sorprendente, tendo en conta que nas Universidades non se impartían cursos ordinarios sobre este tema. En todo caso, contaría coa colaboración de Barrow, tanto na selección de libros como no curso que este impartiu durante un ano. Con todo, é coñecido que pasaron da man de Newton de entón e que tivo una gran influencia de dúas: A Xeometría de Descartes e a dos libros "Arithmetica Infinitorum" de Wallis.

Pero Newton adiantouse a todos en 1665-66 anos, xa que até entón vira como ninguén a clave dos problemas e a solución era dar una regra paira facer a derivada, demostrar que a integral era a inversa da derivada e indicar a vía de aplicación en diferentes problemas.

Newton medía todas as cantidades variables respecto ao tempo (máis tarde dixo que o tempo é calquera cantidade que cambia uniformemente): eran fluentes. As velocidades de cambio denominábanse fluxos. Una curva laun é debida ao movemento da abscisa e a ordenada e tanto x como e teñen os seus fluxos x e e. Dada a ecuación da curva, búscase a relación entre os fluxos. Como o conseguirá? Substituír x e e por x + x ou e e + e ou na ecuación da curva paira acurtar a inicial, dividir por ou e facer 0 esta ou. O método, ademais do estilo, é o actual, coa posibilidade de realizar una derivada implícita.

Por exemplo, paira derivar e = x m/n, aplica o seu método á relación yn = xm: Despois de tratar ambos os lados da igualdade (e + e ou ) n = (x + x ou ) m coa fórmula do binomio, tras dividir e n e x m eliminados por ou, e anular devandito ou, obtén n e n-1 e = m x m-1 x. Basta con substituír e por x m/n,

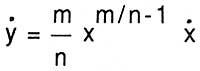
paira ter una derivada coñecida.

O teorema básico do cálculo ou a inversa da integración e a derivación, foi formulado geométricamente por Barrow no libro " Lectiones Geometricae" (publicado en 1670), pero non parece que se apropiase do seu valor. "A fórmula de Newton-Leibniz" é a súa presentación máis sinxela: Se F' = f,

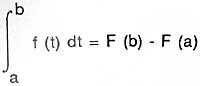
ou ben,

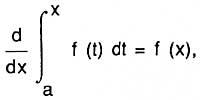
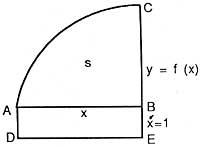
é dicir, a derivada da abscisa da superficie é función (ou ordenada). Vexamos a formulación de Newton. Biz e = f (x) curva e s = superficie (ABC) (ver figura), que se xera polo movemento paralelo da recta vertical BC. Biz x = AB e fagamos o paralelogramo ABED considerando AD = 1. Entón x = superficie (ABDE), esta superficie é xerada polo movemento de VEA. A relación de velocidades de incremento de ambas as superficies, segundo Newton, é igual á relación BC e BE, é dicir, s/x = BC/BE = f(x).

Una vez decidido isto, ao ser máis fácil derivar, a táboa de integrais conterá as derivadas ao revés. Deste xeito, con todo, moitas curvas aínda non poden integrarse e seguindo una idea tomada de Wallis paira ampliar as posibilidades, considerou os desenvolvementos seriados das funcións e seguiunos paira conseguir una nova serie de temas integrados (sen facer caso aos problemas de converxencia, por suposto).

A expansión de (1 + x) m, cando m é total, aínda que se chama binomio de Newton, resulta realmente interesante cando m é incompleto, entón o polinomio non é una serie infinita. m no medio de dous números enteiros (1/2, 3/2, ...) xa se debe a Newton a resposta do caso, xa que demostrou que se aplica a mesma regula que os coeficientes dos polinomios paira os coeficientes.

Co obxectivo de basearse no que se estaba facendo, Newton fará referencia ás relacións dos incrementos: fluxo " a primeira relación dos incrementos emerxentes " ou " a última relación dos incrementos fungibles ". Á vista da imaxe, supoñamos que avanzamos un pouco a abscisa, entón a superficie aumenta e hai que conseguir una relación entre os incrementos de superficie e abscisa, pero a primeira relación flúe é ", antes de comezar a moverse ... Así mesmo, considerando o proceso cara atrás, os incrementos desaparecen e a última relación de incrementos destrutivos " é o fluxo. Pódese suscitar a idea de límite indeterminado.

Hai que compartir as honras

Entre as obras de Newton, as relacionadas co Cálculo son: "De Analysi per Aequationes Numero Terminorum Infinitas" (escrito cara a 1669, publicado en 1711), " Methodus Fluxionum et Serierum Infinitorum" (escrito en 1671, publicado en 1736), " Tractatus de Quadratura Curvarum" (escrito en 1693, páxinas 1704) e "principi" (pp. Como se ve, pasaron vinte anos entre a obtención dos rescatados e o seu despedimento, e así, en 1675, Leibniz chegou pola súa banda a parecidos. O primeiro artigo de Leibniz publicouse en 1684, anticipándose durante tres anos a Principia "".

En 1698 Fatio de Duillier, amigo de Newton, publicou un libro no que lle recoñeceu todo o mérito denunciando que Leibniz fixera plaxio. Leibniz defendeuse a si mesmo e pasaron dez anos ata que o segundo ataque chegou nun artigo de Keill. Este artigo saíu na revista da Real Sociedade e Leibniz, como asociado, solicitou en 1711 ao secretario que aclarase o problema.

Cando o presidente era Newton, nomeouse un comité e a decisión da comisión foi aínda máis dura paira Leibniz. Ademais, decidiron publicar a colección de cartas "Commercium Epistolicum" contra Leibniz. O debate agrandouse e algunhas persoas de Leibniz déronse conta dalgúns erros de Newton. Leibniz, en 1714, escribiu o programa " Historia et origo Calculi differentialis " paira contar a súa verdade. A pesar da súa morte dous anos despois, Newton seguiu atacando.

XX. Até o século XIX este punto estivo sen decidir, pero cando se analizaron os manuscritos de Leibniz recoñecéuselle definitivamente o seu mérito e hoxe a ambos lles corresponde a honra de ser creadores do Cálculo. O debate, con todo, afectou máis a Inglaterra, onde os matemáticos locais e os do continente afastáronse e o desenvolvemento do Cálculo produciuse case na súa totalidade na liña de Leibniz.

Novos camiños e bases sólidas

A difusión do cálculo resultou moi áxil grazas ás revistas de recente creación. Só en revístaa "Acta Eruditorum" hai máis dun centenar de artigos en Leibniz desde o primeiro até os vinte e cinco anos seguintes, a maioría escritos polo propio Leibniz e os irmáns Bernouilli. XVIII. No século XVIII o Cálculo chegaría á cima con numerosos métodos e aplicacións, nos que o nome de Euler debe situarse moi por encima dos seus contemporáneos. Xunto a el destacan a segunda xeración de bernouillitos, D'Alembert e, máis tarde, Lagrange.

Pero o Calculo tiña un pecado orixinal e o bispo inglés Berkeley denunciouno con dureza en 1735, no seu libro " The Analyst ": as últimas relacións das cantidades devastadoras de Newton que se mencionaban na base do razoamento " e os "infinitesimais" de Leibniz eran inaceptables por parte da raíña. En palabras de Berkeley: "O que pode engulir o segundo ou terceiro fluxo e o segundo ou terceiro diferencial non debería preocuparse, na miña opinión, dos problemas da Divindade ", é dicir, un e outro son cuestións de fe. Iso si, non cuestiona os resultados obtidos.

A pesar de que cen anos antes Cavalieri escribira "o erro é un problema dos filósofos e non dos matemáticos", os matemáticos que trataron de construír o Cálculo en bases sólidas, é destacable a importancia dada por D'Alembert ao concepto de limite paira a "Encyclopedie". XIX. A principios do século XX Bolzano, Praga e Cauchy, deron una definición adecuada do límite en París (equivalente ao que existe en calquera libro de hoxe) e a partir del defínese a derivada.

A integral, con Cauchy, pasou de ser a inversa da derivada a definila mediante un limite e entón tivo que demostrar a inversa entre ambas. A Integral seguiu o seu propio camiño e creou a chamada Teoría da Medida; Lebesgue XX. O que terminou a principios do século XX. Ademais da definición xeral da integral, logrou o teorema de diferenciación, a formulación moderna do teorema de Newton-Leibniz.