Xogos matemáticos. Febreiro
1988/02/01 Angulo, Patxi Iturria: Elhuyar aldizkaria
Coñeceredes as seguintes imaxes e asociadas
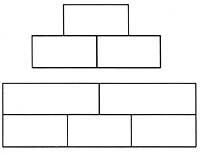
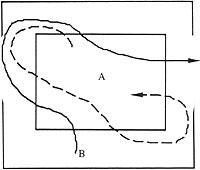
A proposta existente é a de cruzar todos os rectos por unha soa liña, sen cruzar dúas veces ningún deles.
Pódese ver na seguinte imaxe
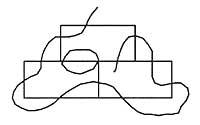
do mesmo xeito que despois de una proba quedouse sen cruzar una recta. Tentada unha e outra vez, non atopamos ningunha resolución. Entón vénnos á cabeza a seguinte pregunta: Ten resolución esta proposta? Neste artigo trataremos de dar resposta a esta pregunta.
Paira iso móstrase na imaxe
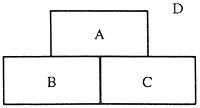
Como as denominaremos comarcas. E paira dicir que pasamos dunha rexión a outra, imos facer o seguinte:
Ao pasar da comarca Á a zona B escribimos AB. Ao pasar da comarca B á comarca C BC, unindo estes dous pasos, é dicir, ao pasar da a B e de B a C escribimos ABC. Como se ve, o paso dun dereito expresámolo con dúas letras. Pero pasar dúas letras en tres. Até agora, ao pasar dunha rexión a outra non dixemos por que dirección hai que pasar, xa que non terá importancia neste razoamento.
Tendo en conta todo isto, ao ser 12 o número de rectificacións que hai que pasar na nosa imaxe, debemos escribir una sucesión de 13 letras paira buscar una solución ao problema. Esta secuencia deberá cumprir una serie de requisitos, como veremos a continuación.
Entre as rexións A e D hai tres directas. Por tanto, AD e DÁ deben aparecer tres veces seguidas. Con todo, a parella AB ou BA só una vez, xa que entre as rexións A e B só hai un dereito. Seguindo o mesmo razoamento, párelos AC ou CA deben aparecer una vez, párelos BC ou CB unha vez e párelos BD ou DB e CD ou DC tres veces. Agora a clave está en atopar una sucesión de 13 letras con estas combinacións. Antes de empezar a buscar esta secuencia, analizaremos si teoricamente é posible ou non.
Si entre dúas rexións e ambas tivésemos un só dereito, estas rexións
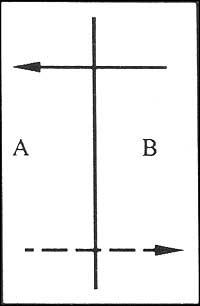
as letras só aparecerían una vez na secuencia de letras: AB ou BA. Pero si tivésemos tres rectos entre ambas as rexións, cada letra aparecería dúas veces: ABAB ou BABA. E si tivésemos cinco directos, veriamos tres veces cada letra: ABABA ou BABABA.
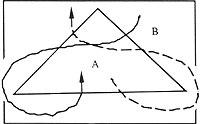
É dicir, en xeral, o número impar n é o número de rectas entre ambas as rexións
se cada letra aparecese n+1/2 veces.
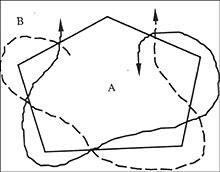
Que ocorrerá cando o número de emendas entre as dúas rexións sexa par? Caso
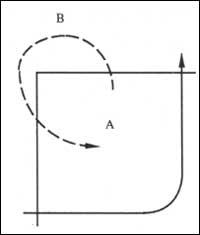
Neste caso teremos que ter en conta a comarca na que empezamos. É dicir, se temos dous directos, se empezamos na comarca A teremos ABA, pero si empezamos na rexión B obteremos BAB. Se tivésemos catro directos A
se empezamos na comarca aparecería ABABA e si empezamos na comarca B obteríase BABAB.
En xeral, se o número de emendas (n) é par, a letra da rexión na que se inicia a liña aparecerá n/2 + 1 veces e a letra do outro n/2 veces.
O que fixemos aquí ocorre con dúas comarcas. Pero cando hai máis de dúas rexións, estes resultados non cambian, xa que ao pasar a un dereito só temos en conta dúas rexións, as que empezan e terminan a liña.
Volvendo á nosa imaxe, temos catro comarcas. As rexións A, B e C están delimitadas por cinco rectas. A comarca D, con todo, nove directos. Aplicando o visto máis arriba, podemos escribir as rexións na primeira columna;

no segundo, o número de emendas que delimitan cada rexión; e no terceiro, o número de veces que debe aparecer cada letra. Sumando os números da última columna conseguimos 14, é dicir, o número de veces que deben aparecer todas as rexións é 14, pero como dixemos ao principio temos que atopar una sucesión de 13 letras. Por tanto, neste caso non hai resolución.
Analizando estes problemas en xeral, dado que o percorrido debe iniciarse nunha rexión e tendo en conta o número de rectificacións que delimitan cada rexión, determinaremos o número de veces que debe aparecer cada letra.
Se n é impar, a letra aparecerá n+1/2 veces. n/2 veces se n é par, se se inicia desde outra rexión ou n/2 + 1 si iníciase nesta rexión. Tendo en conta estes resultados, pódese comprobar que se a suma destes números é igual ao número de rectas máis un, o problema ten una solución. O caso no que a suma é de número de emendas tamén ten una resolución, se a rexión na que se inicia está limitada por un número par de emendas, xa que neste caso a rexión indicada aparecerá n/2 + 1 veces. No resto dos casos non hai resolución.
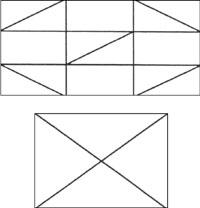
Hai que dicir que esta evasión é a mesma que se deu ao problema das pontes de Koenigsberg exposto no seu día polo matemático Euler. No noso caso as pontes de entón son directos. Paira terminar, aquí tedes dúas imaxes máis para que tentedes atopar a resolución.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia