Denbora-unitateak antzinako Indian

Gaur egungo denbora-definizioak (milurtekoa, urtea, hiruhilabetekoa, bihilabetekoa, hilabetea, astea, eguna, ordua, minutua, segundoa eta beren anizkoitzak eta azpianizkoitzak) naturalki finkaturiko kontzeptuak eta arau zehatzak eta unibertsalak erabiliz zehaztasun handiz definitu direla pentsa daiteke. Nazioarteko unitate-sisteman erabilitako denbora-unitatea segundoa da, eta berau definituz gero, bestelako unitateak modu bakar batean finkatu dira bere anizkoitzak erabiliz.

Dena dela, unitateok ez dira defini daitezkeen unitate bakarrak, eta interesgarri suerta daiteke aipaturiko denbora-unitatea modu berean definitu ez dueneko kulturarik badagoela konturatzea.

Jaipurko behatoki astronomikoan denbora zehatz determinatzeko tresna sofistikatuak aurkitu daitezke. Denbora-unitateei buruzko lehenengo erreferentziak bertsoz sanskritoan idatzi ziren K.a. 1200.etik 600.era bitartean.

Egin-berri dugun (I. R. L.) Indiarako bidaian harriduraz konturatu gara hinduek antzinatik etorri zitzaizkieneko astronomiari buruzko ezagumenduak zeuzkatela. Jaipurko behatoki astronomikoak erabateko zirrara sortu zigun; astroei eta planetei dagokien kokapena zein bi segundorainoko doitasunaz bertako ordua kalkulatzeko (neurketa eguzki-erloju erraldoian burutzen denean) erabil daitekeen aztergailu harrigarrien multzoa ikusita. Behatokiko aztergailuei buruzko zenbait gauza “Elhuyar. Zientzia eta Teknika” aldizkariaren 58. alean argitaratu zen.

Gehien harritu gintuena honako hau da: denbora zehatz kalkulatzeko erakutsi zuten trebetasuna. Harridura areagotu egin zen hinduek urteetan erabilitako denbora-unitateak denboran zehar aldatuz ere joan zirela konturarazi gintuztenean. Kultura honek erabilitako denbora-unitateen laburbilduma egitea erabaki dugu artikulu honetan. Horrez gain, gaur egungo unitate-sistemarekiko baliokideak eta bere izendapenen zenbait eratorri ere aztertuko ditugu.

Antzinako Indiako unitateen gaur egungo baliokideak

Dudarik ez dago Indiako kulturarentzat denbora zehatz neurtzeak garrantzi kulturala duela, gaur egun ere. Astrologiak duen garrantzia historiaurretik datorkiola uste da. Tribuak erreinutan taldekatu eta hazi ahala, zuten gobernua konplexuago bihurtu zen, eta astrologoen boterea eta eragina handiagotuz joan zen.

Vavaha Mihiira astrologo handiak, K. o. 500. urtean bizi izan zenak, astrologoari ondratzen ez zuen erregeari hondamena zetorkiola, eta astrologo bakar bat ehun elefanterekin zein laurehun zaldirekin konparatzerik ez zegoela aipatu zuen bere eskribuetan.

Aditu horien ezagumenduak zenbait liburutan agertu dira, zeintzuetan denbora-neurketak burutzeko arau zehatzak eta erritu eta sakrifizio batzuk burutzeko datuak azaldu diren. Garrantzi berezia zeukaten denboraren determinazioak zein berari zegozkion xehetasunak kalkulatzeko prozedurak. Mendebaldekoak ohituta gaude gure kulturari dagozkion eta unibertsalki finkaturik dauden unitateetan neurketak burutzen. Denbora-unitateak zehazki finkatzea posiblea da gaur egun, eta informazio hori munduko edozein puntutan baliagarria da. Nazioarteko sisteman oinarrizko unitatea segundoa da. 60 segundok minutu bat osatuko dute, era berean 60 minutuk ordua, eta 24 orduk eguna. Unitate handiagorik ere badugu: astea (7 egun), hilabetea (30 egun), urtea (365 egun), milurtekoa, etab.

Elefante bakar batek gidaria eta lau turista ere garraia ditzake. Ehun elefante ere ezin konpara daitezke astrologo bakar batekin.

Hala ere, aipaturiko unitateak ez dira unitate bakarrak eta historian zehar aldatu egin dira. Indiaren kasuan, denbora-unitateak oso desberdinak zirela aipatu behar da. Unitateak zeintzuk diren, beren izenak eta neurketa-prozedurak, eta herri batetik beste batera beraiei buruzko ezagumenduak transmititzea nola lortu zuten aztertzea erabaki dugu. Horretarako, denbora-unitate eta gaur egungo sistema-unitateekiko baliokideak finkatu dituzten iturri desberdinetatik zenbait datu jaso dugu.

Erreferentziaturiko eskuskriburik zaharrena, Vedanga Jiotisa delakoa, bertsotan sanskritoz idatzita dago, eta K.a. 1200. urtetik 600. urte bitartekoa da. Orduko ohiturari segituz, maisuak (guru zelakoak) ikasleari (shishia zelakoari) berak zituen ezagumenduak ahoz erakusten zizkion, bigarrenak buruz ikas zitzan. Lana errazteko bertso eran idatzi ziren eskribuak.

Aipatzen den lehen denbora-unitatea 5 urteko zikloa da (juga), Muga delakoaren ilberan (urtarrila-otsaila) hasi eta Pausa delakoaren ilgoran (abendua-urtarrila) bukatzen delarik. Urteari 183 egunez (savana divasa) osaturiko bi zati (aiana) dagozkio, non eguna (nitemeron) egunsentitik hurrengo egunsentirarteko denbora tartea den.

Eguna baino tarte txikiagoei dagozkien denbora-zatiketei buruz arituko gara. Ezagutzen diren erreferentziak, K.a. 1200. urtetik 1030. urte bitartekoak dira, eta askotan denbora-unitatea izendatzeko eran edo definitzeko moduan ez datoz bat.

Datuon laburbilduma ondorengo taulan aurkezten da.

Ur-erlojua erabiliz ontzi desberdinei dagozkien ur-mailaren erorketak. a) ontzi zilindrikoa, b) ontzi erdiesferikoa (kapala).

Oro har, zenbait definiziotan ezaugarri amankomunak aurki ditzakegu. Ondoren azalduko dugu. Denek egunaren edo hogeitalau orduren (nitemeron) denbora-tarte baliokidea dute barnean. Eguna, hirurogei aletan zatitu dute (nadi, nadika, gati, gatika, danda, data), ondorioz lortu duten denbora-unitatea hogeitalau minututakoa delarik. Era berean, aipaturiko denbora-unitatea hirurogei tartean zatitu dute, hogeitalau segundoko denbora-unitatea lortuz (vinadi, vinadika, pala, cashaka). Arnasketa, edo hamar silabako (gurvak-shara) hitza ahozkatzeko behar den denbora-tartea definitu dute unitaterik txikien gisa, non denbora-unitate hori arestian definiturikoaren seirenarekin bat datorren.

Beraz, bere balioa lau segundokoa dela esan dezakegu. Datu bitxia aipatzekotan, honakoa esan daiteke: egunean dagoen prana-kopurua eta zirkunferentzian dagoen minutu-kopurua berdinak dira. Erlazioa ez da dirudien bezain halabeharrezkoa. Ez dezagun ahaz, soluaren gaineko itzalari dagokion proiekzioaz baliatutako eguzki-erlojua zela Indian denbora neurtzeko modurik erabiliena.

Lau segundo baino unitate txikiagoak finkatzea oso zaila zen; besteak beste, horretarako zeuzkaten bideak berregiteko errazak ez zirelako. Horretan datza aipaturiko denbora-unitateen balioen arteko aldea.

Ur-erlojuak

Denbora-tarte laburrak, prasta izenekoaren modukoak, eguzki edo beste zenbait izarren higiduren behaketetan oinarritu beharrean ur-erloju mekanikoak erabiliz neurtu ziren. Astrologiak finkatu eta izar- eta planeta-kokapenei dagozkien denbora absolutuaren beharra soilik ez zeukan hinduen errituak. Sakrifizioen segida erregulatuko zuen erlojuaren beharra ere bazeukan errituak. Helburu hori betetzeko ur-erlojuak (Jalaiantra izenekoak) erabili ziren.

Erarik errazena, klepsidra helenikoaren baliokidea zena, hondoan zulo txiki bat zeukan urez beteriko ontzian zen. Al-Biruni-ren hitzak gogoratuz:

“Kaxmirko Uptala-ren Surdava izeneko liburuan irakurriz: egur-zatian hamabi atzamarreko diametrodun eta sei atzamarreko altueradun zulatutako hutsuneak hiru ur-mana dauzka. Hutsunearen hondoan emakumezko gaztearen, ez zaharren ez eta neskatoren, sei ile bezain handia den zuloa egingo balitz, hiru ur-manak gati batean eroriko lirateke zuloan zehar.”

Gaur egungo astrologoek desegokitzat hartuko lukete erloju hori, tentsioaren eraginak aparte, ontziko uraren maila ondoko lege esponentzialari jarraituz txikiagotuz doalako:

H = H₀ exp(-ct),

Goniometroaren (triangelu-forma duen hormaren) proiekzioari dagokion itzalean datza eguzki-erloju erraldoia edo Samrat Jantra. Argazkia arratsaldez hartu zen.

non c, zuloaren diametroarekin ezezik, beste zenbait faktorerekin ere (hots, ur-dentsitatearekin eta biskositatearekin, erlazionaturik dagoen. Ontzia denbora infinituan hustuko litzateke. Gainazal-tentsioaren efektuaren eraginez fluxua moztu egingo da, ur-bolumen txikia hutsunean atxekiko delarik.

Neurketaren xehetasunak kanporatutako fluidoari dagokion kurbaren maldarekiko alderantzizko menpekotasuna daukanez, azkenean kronografo hinduek prozedura hori utzi egin beharko lukete.

Aipaturikoa egin beharrean eta ur-erloju egiptiarraren kasuan ez bezala, (zeinetan fluidoaren erorketa-denbora ontziaren barnean urak lorturiko mailari zegokion irakurketaren bidez egin zen) eroritako ura bolumen zehatzeko (prasta bateko) ontzian bilduko zen. Prasta zelako denbora-tarte hori beren ospakizunetarako soilik neurtzea interesatzen zitzaienez, nahiz eta bolumen-unitatea izan, denbora-unitate bihurtu zen. Ontzian zegoen ur-maila konstante eta altuera egokian mantenduko zela uste da.

Erloju hori historian zehar hobetu egin zen, eta dirudienez, bertsio berria maiz erabili zen XII. mendearen hasieratik Europako erloju mekanikoak azaldu bitartean. Erabilitako ontziak (gati-ak), definitu zuen denbora-tarteari izena eman zion. Dirudienez, aurreko nadika-ren baliokidea zeneko eta hogeitalau minutuko iraupena zeukaneko gati-ak prasta zelakoa ordezkatu zuen.

K.o. 1603. urte inguruan Ranganata-k idatzitako Suria Sidantari zegokion irazkinean ontziaren dimentsioak zehaztu dira: “Sei atzamarreko (angula) altuera eta ertzean neurri horren bikoitza zuen esferaerdi (kapala) zen ontzia, hirurogei ur-pala-ko edukiera zeukalarik. Lau atzamarreko luzera eta hiru masha eta hereneko pisuko urrezko orratza pasatzeko modukoa zen hondoko zuloa.”

Urteetan zehar pisu- eta neurketa-sistemak balioz eta izenez aldatu egin dira, eta kasu bakoitzari dagokion gaur egungo neurriaren baliokidea ezagutzea interesgarria da. Eskua zabal zabalik edukita orduko hinduen atzamar loditik txikirainoko luzeraren balioa 22,8 cm-koa zela kontutan hartuz, angula-ren balioa 1,9 cm-koa dela esan daiteke. Ontziaren bolumena kalkulatutakoan, ondokoa ondoriozta daiteke:

1 pala = 51,7 cm³

edo,

1 pala = bolumena = 1/2 1/4 πr³
60

non r = 11,4 cm den.

Bestalde, Varaha Mihiira zenaren kasuari dagokionez, pisu-sistema ziape-hazian eta hori baino zortzi aldiz astunagoa zen arroz-garauan datza. Bere oinarrizko baieztapena balioztatzeko, 1 pala-k 52,096 g-koa izan beharko luke. Eskribuen arabera, orduko ziape-haziak 3,7 mg-ko pisua zeukala ondoriozta dezakegu. Dirudienez, urteotan nabarmen aldatu ez den balioa da. Hala ere, masha delakoa ezin aurki daiteke inolako eskributan.

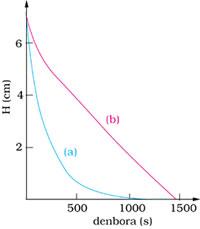
Ur-erorketaren abiadurak ez dauka ebazpen analitiko errazik. Hamar pala-ko ontziko uraren altuera azkar txikiagotuko da denboran zehar, goiko (b) irudian ikus daitekeenez, eta zerora heldutakoan hustuko da ontzia. Tartearen bukaeran, kurbaren maldak balio finitua du, klepsidra delakoaren kasuan lortutako balioarekin konparatuz desberdina delarik, eta horrela, azken puntua determinatzeko erabilitako prozedurari dagokion xehetasunak gehikuntza nabarmena jasango duelarik. Ontzia gati batean hustu dadin, masha baten balioak 0,18285 g-koa izan behar du, eta % 0.1-eko pisu-aldaketak hamasei segundotan aldatuko du emaitza.

Surdava ur-erlojuaren kasura itzuliz, kalkulu errazaren bidez 1 mana-ren baliokidearen balioa ondoriozta daiteke:

1 mana = bolumena = 1/3 πr2h
3

non r = h = 11,4 cm. den. Beraz, 1 mana = 4.654 kg da; hots, gutxi gorabehera 30 pala direlakoen pisu berekoa da. Hala ere, Al-Biruni-k berak ere 1 mana eta 15 pala berdinak direla ziurtatu du.

(1)VEDANGA JIOTISA (K.a. 1200-600)
(2)PURANA (K.o.?)
(3)VISHNU PURANA (K.o.)
(4) SURIA SIDANTA (<400 K.o.)
(5) SURIA SIDANTA delakoen bilduma (<400 K.o.)
(6) YUANG CHWANG (K.o. 629)
(7) AL-BIRUNI (K.o.1030)

juga aiana savana divasa	6 urte 1 urte 1/2 urte (1)	(2)	(3)	(4)	(5)	(6)	(7)
nictemeron	eguna	eguna	eguna	eguna	eguna	eguna	eguna
trimaia time watch muhurta	- - - 48 min	- - 4 ordu 48 min	- - - -	- - - -	- - - -	12 ordu 4 ordu - 48 min	- - - -
nadi nadika gati gatika danda data	- 24 min - - - -	- - - - - -	- - - 24 min - 24 min	24 min 24 min 24 min 24 min - -	- - - - 24 min -	- - - - - -	- - 24 min - - -
lava prasta	- 1 min 34 s	- -	- -	- -	- -	1 min 36 s -	- -
vinadi vicala vinadika pala cashaka	- - - - -	- - - - -	- - 24 s 24 s -	24 s - - - -	- 24 s - - -	- - - - -	- - - - 24 s
prana (arnasketa) asu	- -	- -	4 s -	4 s 4 s	4 s -	- -	4 s 4 s
kasta gurvakshara (silaba) tatkshana akshara nimesha kshana hsun truti (balio teorikoa	1,15 s - - 0,23 s - - - = 33 μs	3,18 s - - - 0,21 s - -	- 2,4 s - - - - -	- - - - - - -	- - - - - - -	- - 1,6 s - - 0,013 s keinua	- - - - 6 min -

Angelu/Denbora erlazioa Gainazalaren gaineko gorputzaren itzalaren bidezko denbora-neurketak burutzeko, astronomo hinduek distantziak neurtzeko erabilitako neurriak ezagutzea beharrezkoa da. Oro har, gainazal esferikotan (Kapala Jantra), zirkularretan (eguzki-erloju edo Samrat Jantra), gurpiletan (Txakra Jantra) edo marra kurbatua irudikaturik zueneko planoan proiektatzen ziren itzalak. Kasu guzti horietan, zirkunferentzi angelu edo erdiesfera-angelu modura neurtuko dira distantziak. Hala ere, angelu-neurketak ez datoz bat gure sistema hirurogeitarraren gradu, minutu eta segundoekin. Ondoko irizpidea erabili zuten: zirkunferentzia hirurogei gati-tan zatituko da; modu berean, gati-ari hirurogei pala dagozkio. Azkenik, sei prana daude pala-ko (sei minutu). Beraz, prana bat minutu bat da. Zirkunferentzia zen ganga zerutarren adierazpena. Angeluren bat betetzeko itzalak behar duen denbora-tartea denbora-unitate modura definituz, modu bakarrez erlaziona daiteke osaturiko angelua eta behar izan den denbora. Horregatik, angelua zein berari zegokion denbora-tartea adierazteko hitz berbera erabili zen kasu askotan. Ondoko taulan baliokideak laburbildu dira. ANGELUA DENBORA IZENDAPENA 1 gati = 6 gradu 1 pala = 6 min 1 prana = 1 min 24 min 24 s 4 s nadi, nadika, gati, gatika, danda, data vinadi,vicala,vinadika, pala, cashaka, prana, asu Planetak ekliptikatiko 5° edo 10° baino distantzia handiagotan inoiz kokaturik ez daudelako, definizio hori oso erabilgarria zen astronomo hinduentzat. Gainera, planetak kokatzeko ere erabil zitzaketen aipaturiko unitateak. Zeruko gorputzei dagozkien longitude eta latitudeak ezagututa, planetak identifika zitzaketen mailakatutako goniometroaren laguntzaz. Ohar garrantzitsu batez buka dezakegu atal hau: goniometro hinduen bidezko angelu-neurketak burutzerakoan, kontuz unitateekin!!.