Poliminoak (I)

omino hitza Latineko dominusetik dator eta Jaun esan nahi du. Hala ere guk beste jatorri bat asmatuko diogu: Domino = dos minos, hain zuzen.

Domino 28 piezaz osatutako joko ezaguna dugu. Domino hitza Latineko dominusetik dator eta Jaun esan nahi du. Hala ere guk beste jatorri bat asmatuko diogu: Domino = dos minos, hain zuzen. Hau da, Dominok bi mino esanahia leukake. Jokoaren piezei begira, denak bi laukiz osatuak direla ohartuko zara. Hortaz, gure hipotesiari jarraituz gero, mino hitzari lauki hitza legokioke.

Hau izango da, hain zuzen ere, dominotik beste poliminoak eraikitzeko aitzakia. Hemendik aurrera domino jokoaz ahantzi egingo gara eta bere egituraz arduratuko gara, beti "mino = lauki" denaren hipotesiaren mende.

Bi mino erantsiz, pieza bat lortzen da. Itxura aldetik, pieza bakarra da edozein eratara eransten badira ere. Pieza horri domino esango diogu eta formaz bakarra denez ez du joko handirik ematen.

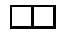
Aurrera jarraitu baino lehen, ohar bat egingo dizugu: posible diren simetria (planoan) eta biraketa (plano eta espazioan) guztien bidez lortutako piezak berdintzat joko ditugu. Geroago adibide bat jarriko dizugu erraz uler dezazun.

Ekin diezaiogun triminoak eraikitzeari. Horretarako dominori beste mino bat erantsiko diogu, ondoko bi trimino ezberdin lortuz:

Triminoek ere ez digute joko handirik ematen. Hala ere, bi pieza hauekin zenbait irudi egin daiteke, ondoan ikusten den bezala:

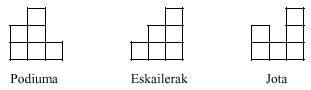
Ezin da, ordea, 2x3 dimentsioko laukizuzena egin, erraz egiazta daitekeenez.

Pasa gaitezke, beraz, hurrengora; tetraminoetara alegia. Tetraminoak osatzeko, triminoari beste mino bat atxekiko diogu era guztietara:

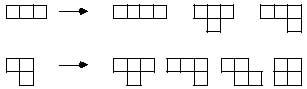
Berdinak kenduz gero bost tetramino ezberdin lortzen dira:

Bost tetraminoek 20 mino biltzen dituzte guztira. Hauekin 2x10 eta 4x5 neurriko laukizuzenak egin daitezke. Hala ere, bost tetraminoez ezin dira osatu ez bata eta ez bestea. Aldiz, bost piezekin beste irudi hauek egiterik badago:

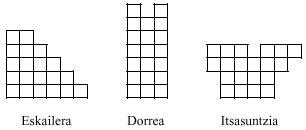
Egin dezagun aurrera pentaminoak osatuz. Berriro ere tetraminoei mino bat atxekiko diegu; era guztietara:

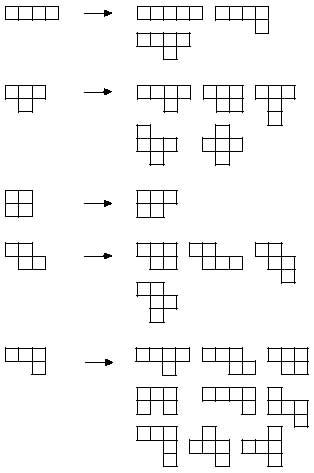
Hauetan ezberdinak bakarrik aukeratuz, 12 pentamino lortzen da:

Orain ikus dezagun hasieran agindutako adibidea:

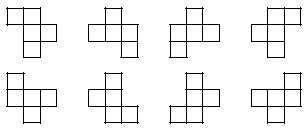
Irudian agertzen diren pieza guztiak berdintzat hartzen ditugu.

12 pentaminoekin 60 mino biltzen dira eta hauekin 2x30, 3x20, 4x15, 5x12 eta 6x10 neurriko laukizuzenak egin daitezke. Agerian dago lehenengoa 2x30 pentaminoez ezin dela osatu; piezen erdiak 3 zabalera behar bait du bi norabideetan. 3x20 dimentsioko laukizuzenerako soluzio bat aurkitu dugu eta ez dugu bakarra denik uste.

4x15 neurrikorako ere beste soluzio bat badaukagu. 5x12 neurrikorako, aldiz, ez dugu soluziorik aurkitu. Gure saioa ez da erabatekoa izan. Hortaz, ezin dugu soluziorik ez daukanik esan. Zeuk baten bat aurkituko bazenu, eskertuko genizuke guri bidaliko bazenigu.

6x10 dimentsioko laukizuzenaz informazio gehiago daukagu, eta honakoa baiezta dezakegu: soluziorik badagoela eta ez dela bakarra; simetrikoez aparte soluzio ugari daukala (1.000 baino gehiago), pentamino jokoa ekoizten duen marka baten aurkezpenean agertzen den bezala.

Laukizuzenez gain badaude pentaminoez osa daitezkeen beste irudi batzuk. Honen lekuko ondoko irudiak:

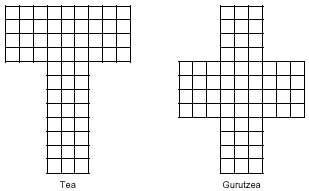
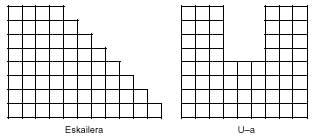
Pentaminoetatik abiatuz 119 hexamino lortzen dira, zeintzuetan ezberdinak 35 bakarrik diren. 12 pentaminoak erabiltzea jadanik zaila bada, pentsa ezazu 35 examino maneiatzen zer gerta dakizukeen. Dena dela, ausarta bazara, hemen dauzkazu 35 hexamino ezberdinak:

35 hexaminoetan 210 mino dagoela kontutan hartuz, 2x105, 3x70, 5x42, 6x35, 7x30, 10x21 eta 14x15 neurriko laukizuzenak osa daitezke. Aurreko kasuetan bezala, lehenengoa ezin da osatu hexaminoez. Ez dakigu besteak osa daitezkeen ala ez. Hor daukazu lana, jakinminik baduzu. Irudiko hexaminoetan, zeintzuk dira tolestuta hirudimentsioko kuboa lor daitezkeenak?

Badaude poliminoekin jolasteko beste aukera batzuk ere. Berriro ere domino, trimino eta tetraminoak baztertu beharrean gaude, aukera gutxi ematen digute eta. Aldiz pentamino eta examinoak egokiak dira, pieza-kopuru aldetik, hurrengo jokoan aritzeko.

Pentaminoekin jolasteko 8x8 laukitxoko taula bat (xakekoa) erabiliko dugu, eta laukitxoen neurriak mino-arenak izango dira.

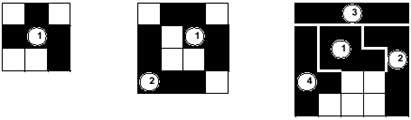
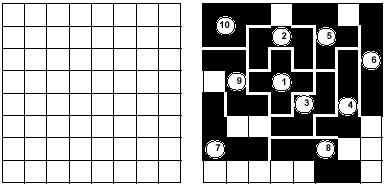
Jokoak modalitate ugari onartzen badu ere, funtsean ez da aldatzen. Jokalariek (bi, hiru, lau,...) piezak txandaka ipini behar dituzte taulan. Azken pentaminoa jartzen duenak irabaziko du. Irudiko adibidean bi jokalariren arteko partida bigarrenak irabazi du; azken pentaminoa (10) ipini bait du. 12 pentaminoak jokalarien artean bana litezke zoriz, edo beste posibilitate bat jokalariek piezak pilo beretik aukeratzerik izatea da. Bikoteka ere jolas liteke aurrerko bi eratara.

Taularen neurriak ere alda litezke. Neurririk txikiena 3x3 da, zenbait piezak hala eskatzen duelako. 3x3 dimentsioko taulan jokoak ez du mamirik; lehenengo jokalariak beti irabazten bait du, taula horretan pentamino bat bakarrik sartzen da eta. 4x4 dimentsioko taulan, aldiz, bigarren jokalariak irabaziko du beti. Honekin zera esan nahi dugu: lehenengo jokalariak nahi duen pieza aukeratzen badu ere, bigarrenak beti izango duela azken pieza ipintzeko aukera. Horrez gain, kasu batean ezik beste guztietan bigarren jokalariaren aukera ez da bakarra izango. Zuri uzten dizugu kasu berezi hori (2. jokalariak aukera bakarra duen kasua) asmatzea.

5x5 dimentsioko taulan lehenengo jokalariak irabaziko du beti, lehenengo pieza ondo aukeratuz gero. Zein da pieza hori?

Hemendik aurrera dimentsio handiagoko tauletan posibilitateak ugaldu egiten dira eta zaila da azterketa zehatza egitea. Bestalde, taulak ez du laukia zer izanik eta beste neurritakoak ere aukera litezke; esate baterako, 5x6, 3x20, 4x15, 5x12 edo 6x10 laukizuzenak. 5x6 dimentsioko taulan badago lehenengo jokalariak beti irabaz dezan jokaldi egoki bat. Zein da?

Hexaminoekin jolasteko gauza bera egin daiteke. Kasu honetarako azterketa, bukaezin bihurtuko litzateke; 35 pieza bait daude. Bestalde aukera gehiago eskaintzen du pieza-kopuru aldetik. Horra hor 14x15 dimentsioko laukizuzena hexaminoekin jolasteko.