Astronomie XVII. siècle siècle siècle siècle siècle siècle siècle siècle siècle

1991/05/01 Bandres Unanue, Luis Iturria: Elhuyar aldizkaria

• Astronomia
• Historia

La théorie du mouvement des planètes a maintenant eu un développement énorme. Nous sommes en 1600. La Renaissance et la Réforme sont en cours. Dans le domaine de l'astronomie, certains utilisaient les avantages de calcul offerts par le système de Copernic, mais sans accepter ses conséquences tant physiques que philosophiques. Dans ce silence, une seule voix exprimait le conflit qui venait. Giordano Bruno (panthéiste anti-orthodoxe et transeuropéen) disait que les limites de l'univers étaient très loin (c'est-à-dire dans l'infini) et que notre système solaire n'est qu'un système parmi d'autres infinis. Pour toutes les hérésies mentionnées, l'Inquisition a jugé et brûlé en 1600.

Cependant, les graines d'une nouvelle science germaient partout. En Angleterre Francis Bacon (1561-1626) et William Gilbert (1540-1603); en Italie Galileo Galilei (1564-1642); à Copenhague Tycho Brahe (1546-1601). C'est le premier homme qui, depuis l'époque grecque, a apporté des améliorations aux observations astronomiques. Presque toute sa vie, avec une précision qui jusqu'alors n'était pas la même, est passée à observer les mouvements des planètes. Ses données étaient souvent vingt fois plus précises que celles de Copernic, et tout cela sans inventer le télescope.

Après la mort de Tycho Brahe, l'Allemand Johannes Kepler (1571-1630) lui donna la suite d'une part en faisant d'autres observations et d'autre part en effectuant une enquête approfondie sur toutes les données prises. Tandis que Tycho développait en son temps un système planétaire spécial, Kepler était en faveur de Copernic. Le but de ses travaux était de faire plus précis que les tables astronomiques des mouvements des planètes dans cette période. Mais il ne voulait qu'adapter la théorie héliocentrique à la base, parce que par son harmonie et sa simplicité, il la voyait fascinée et à son goût. Dès le début de ses œuvres, la métaphysique pythagoricienne et la néoplatonicienne eurent une grande influence. Cette tendance a continué pendant la Renaissance défiant l'hégémonie aristotélicienne.

Selon Kepler, la tendance de l'intelligence divine était en quelque sorte géométrique et les caractéristiques de cet ordre pourraient être trouvés dans les relations mathématiques qui conduisaient le système héliocentrique. Par conséquent, dans l'un de ses premiers travaux, il a cherché à relier les six planètes connues et leurs distances au Soleil avec les cinq solides réguliers de la géométrie.

Quand il voulait adapter les nouvelles données obtenues de l'orbite de Martitz au système de Copernic et après quatre années de dur labeur, il est arrivé à une conclusion très importante, qu'il était impossible! Les nouvelles données situaient l'orbite à huit minutes du schéma de Copernic. Bien que Copernic à son époque, sachant que les données utilisées n'étaient pas exactes, il n'a pas donné d'importance à cette différence, Kepler savait que les données de Tycho étaient beaucoup plus exactes que la différence mentionnée, donc ce qu'il a obtenu était inacceptable. C'est pourquoi, et avec l'honnêteté qui correspond aux scientifiques, ils n'ont pas essayé de nier les observations et d'inventer de nouvelles hypothèses pour sauver la théorie acceptée par eux-mêmes. Cependant, pour lui ces huit minutes indiquaient : Que le système de Copernic n'était pas en mesure d'exprimer le mouvement réel de Mars. Il a donc abandonné le système de Copernic avec ses sphères concentriques et épicycles.

Pour Kepler ce serait très dur, parce qu'il était un partisan du système de Copernic. Cependant, il a continué et pour cela a dû briser le joug qui unissait le système de Copernic avec la Grèce antique. Quand il a étudié les trajectoires des planètes selon la théorie héliocentrique, il est venu à l'idée que l'image des parcours pourrait être de l'ellipse (caractéristiques de l'ellipse a. C.). II. Ils étaient connus depuis le XIXe siècle). Si on acceptait cela, c'est-à-dire que le parcours naturel d'une planète est ellipse, on construisait un schéma géométrique d'une grande facilité pour le monde. Dans ce schéma, toutes les planètes se déplacent en orbite elliptique, avec le Soleil dans un foyer. Cette loi est l'une des trois principales lois de Kepler et est généralement dit être le premier.

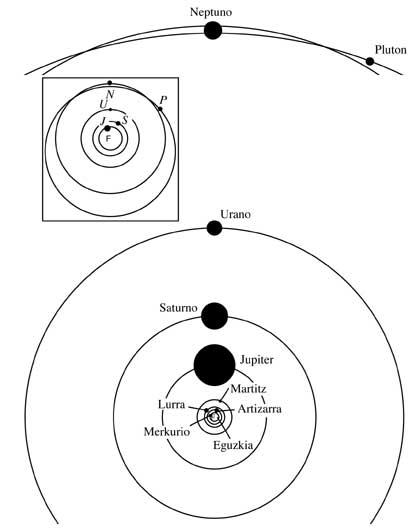
Cette première loi de Kepler, en dirigeant la théorie héliocentrique de Copernic, nous donne une image très simple du système solaire. Tous les épicycles et excentriques de Copernic sont écartés : les orbites ne sont que des ellipses. Dans l'image, vous pouvez voir le schéma actuel et simple du système solaire

Ces ellipses sont presque cercles et toutes les orbites sont presque sur le même plan, sauf pour Pluton. Cela a une forte inclinaison et dans l'image comme dans d'autres, les orbites de Neptune et de Pluton ne s'humilient à aucun point de l'espace.

Probablement Kepler était heureux d'arriver à une conclusion aussi simple que celle-ci (après avoir renoncé aux épicycles et excentriques qui étaient très compliqués), voyant que tout s'accomplissait bien à travers les ellipses. Cependant, en elle-même avait une préoccupation: nous pouvons comprendre la tendance de Platon à reconnaître que les mouvements circulaires et uniformes étaient naturels, mais pourquoi la nature choisit l'ellipse? Pour répondre correctement à cette question, il faut attendre l'arrivée de Newton, qui nous a dit que la loi de l'ellipse est une conséquence d'une autre loi de la nature beaucoup plus large. Par conséquent, laissons le sujet pour l'instant.

Nous devons donc penser que la première loi de Kepler est un résumé des observations faites, c'est-à-dire une loi empirique. Mais, bien que cette loi nous rende compte de tous les endroits d'une planète, elle ne nous dit rien au sujet de quand cette planète sera dans l'un ou l'autre endroit, c'est-à-dire nous indique l'image de l'orbite, mais sa vitesse ne sera pas. Par conséquent, cette loi est très courte car les astronomes (et Kepler aussi) veulent savoir à l'avance quand ce sera une planète à un moment donné. C'est pourquoi, avant sa première loi, Kepler avait établi une deuxième loi qui nous indique les changements de vitesse d'une planète.

Kepler savait que s'il existait une relation mathématique entre la vitesse d'une position à l'autre de l'orbite d'une planète, le système serait beaucoup plus simple. Si cette relation était découverte, le mouvement d'une planète pouvait être exprimé avec très peu de données. Deux données étaient nécessaires pour fournir la même ellipse, le troisième pour atteindre la vitesse à un point précis du parcours (dans le périhélium, par exemple, le point le plus proche du Soleil) et un autre pour connaître l'inclinaison du plan orbital par rapport aux autres planètes. Mais personne ne connaissait cette relation. C'est pourquoi, quand cette loi lui est venue, on dit qu'il était dans l'extase, mais ce que nous savons, c'est que pour la trouver, il a dû analyser beaucoup de données et effectuer un travail constant et dur.

En tout cas, la voie qu'il a suivie pour obtenir cette deuxième loi est surprenante, car sur la base des trois hypothèses erronées est venu à sa conclusion. Selon les mots de Kepler, l'orbite décrivant les planètes est due à la force exercée par le Soleil et dont la valeur était inversement proportionnelle à la distance entre le Soleil et la planète. La vitesse et la force qui anime la planète étaient directement proportionnelles les unes aux autres et donc inversement proportionnelles à la distance. Cette hypothèse (c'est-à-dire que la vitesse soit proportionnelle à la force) est aujourd'hui inacceptable, mais on peut le voir comme l'idée d'Aristote ou comme quelque chose que le bon sens donnait à cette époque.

Selon cette hypothèse, le temps que prend une planète à parcourir une petite distance pendant le parcours serait proportionnel à la distance au Soleil. C'est presque totalement correct et ainsi à quelques points de l'orbite. Par conséquent, Kepler voulait calculer le temps nécessaire pour compléter un grand parcours (et donc lorsque la distance au soleil est variable). Pour cela, il a pris en compte les distances de tous les petits arcs qui forment ce grand tronçon et a conclu que ce temps est directement proportionnel à la surface qui couvre la ligne allant du Soleil à la planète. Selon cette deuxième loi, la Terre (ou si l'on veut le Soleil au fond des étoiles) est entendu qu'en hiver elle bouge plus vite qu'en été, ce que Kepler et ses prédécesseurs connaissaient parfaitement.

Les deux lois ont été publiées en 1609 dans le livre Astronomy Nova. Mais Kepler n'aimait pas et avait une préoccupation : on ne connaissait aucune relation entre les mouvements des différentes planètes. Chaque planète se déplaçait sur son ellipse et à sa vitesse, mais il semble qu'il n'y avait pas de modèle général pour tous. Kepler pensait que ce modèle général devait exister, il devait donc y avoir une relation qui relie tous les mouvements présents dans le système solaire. Kepler partit après cette relation et utilisa pour cela la théorie musicale, selon les disciples de Pythagore, à la recherche d'un lien entre les orbites des planètes et les notes musicales. Si son œuvre prolifique était appelée Harmonie du monde, il voulait exprimer quelque chose.

Croire en cette relation (ou plutôt son obsession) peut, d'une part, exprimer la première foi magique des nombres que Kepler avait, mais aussi la tendance de tous les génies de la science. Selon eux, la nature est uniforme et simple. Cette croyance a donné une grande aide aux scientifiques et une force pour surmonter les obstacles. C'est le cas de Kepler qui, après avoir découvert sa troisième loi pour avoir subi mille malheurs personnels, a pu écrire:

... après avoir longtemps trouvé une distance réelle des orbites en utilisant les données de Brahe, une relation réelle... le fait qu'il y ait un si large consensus entre le travail que je présente aujourd'hui et le travail que j'ai fait pendant dix-sept ans sur les observations de Brahe, a nettoyé mes ombres de mon esprit et je pensais qu'au début j'étais dans mes rêves...

Selon la langue actuelle de cette loi, si la période d'une planète est T (c'est à dire le temps de faire un tour complet autour du soleil) et R son rayon moyen, T ² = K . R est 3, ^K étant une constante égale pour toutes les planètes. Dans le cas de la Terre T = 1 an et R = 15 x 10 ⁷ km, donc si nous connaissons votre radio R pour toute autre planète, nous pouvons trouver la période.

Cette troisième loi est appelée loi harmonique, car elle représente une belle relation harmonieuse entre les planètes.

À travers tout cela, en reliant logiquement notre système solaire, nous le voyons comme un tout simple : notre intelligence capte l'univers de Kepler avec un regard et est capable d'exprimer mathématiquement les lois qui le régissent.

Kepler, à partir des données de Brahe, a essayé de construire des tableaux détaillés des mouvements planétaires. Pour mener à bien ce travail, il a dû abandonner certaines des opinions acceptées à cette époque. Cette attitude était complètement nouvelle, c'est-à-dire donner la priorité aux observations, si celles-ci étaient effectuées de manière précise et quantitative. Un autre aspect à noter est la prédiction de l'utilisation du langage mathématique dans l'expression des lois physiques. Par la suite, les équations seraient les expressions naturelles des lois physiques.

D'autre part, le mouvement des planètes dans leur orbite dans le système de Kepler n'était pas considéré produit par aucun dieu (comme le montraient les scolastiques), ni par leurs formes sphériques représentaient des mouvements circulaires. Dans son dernier livre ( Mysterium Cosmographicum ), il nous raconte comment il a changé ses opinions en 1596:

À une époque, je croyais fermement que la force du mouvement d'une planète était dans une âme... Cependant, quand j'ai pensé que cette cause du mouvement diminuait avec la distance (c'est-à-dire que la lumière du Soleil diminue avec la distance à cet astre), j'ai conclu que cette force devait être substantielle, pas littéralement, mais… comme nous disons que la lumière est quelque chose de substantiel, c'est-à-dire quelque chose de non spirituel et qui sort d'un corps substantiel.

En 1605, il écrit à un ami:

Je me suis beaucoup occupé de la recherche de causes physiques. Mon essai a consisté à démontrer que la machine céleste doit être comparée à un organisme divin et non à une œuvre d'horlogerie (et qui croit qu'une montre a une âme, attribue l'honneur à l'horloger), et que dans cette montre tous les mouvements différents sont le résultat d'une simple force magnétique, comme tous les mouvements de la machine d'une montre sont la conséquence d'un poids unique. En outre, je démontre que cette conception physique doit être exprimée par calcul et géométrie.

A Kepler, nous pouvons voir clairement le changement commencé en Europe deux siècles plus tôt. L'observation quotidienne, les résultats, en définitive, laissent place aux simples spéculations et les théories doivent se fonder sur cette réalité. C'est pourquoi nous pouvons dire que Kepler a fait une première revendication de l'attitude moderne de la science.