Astronomy XVII. century
1991/05/01 Bandres Unanue, Luis Iturria: Elhuyar aldizkaria

The theory of the movement of the planets has now had an enormous development. We are in the year 1600. Both the Renaissance and the Reformation are happening. In the field of astronomy, some used the calculation advantages offered by the Copernicus system, but without accepting its physical and philosophical consequences. In this silence one voice was heard expressing the coming conflict. Giordano Bruno (anti-Orthodox and trans-European pantheist) said that the limits of the Universe were far (i.e. in infinity) and that our Solar System is only one system among other infinite. For all the heresies mentioned, the Inquisition judged and burned it in 1600.
However, the seeds of a new science were germinating anywhere. In England Francis Bacon (1561-1626) and William Gilbert (1540-1603); in Italy Galileo Galilei (1564-1642); in Copenhagen Tycho Brahe (1546-1601). He is the first man to make improvements in astronomical observations since Greek times. Almost all his life, with a precision that until then was not the same, he went on to observe the movements of the planets. His data were, on many occasions, twenty times more accurate than those of Copernicus, and all this without inventing the telescope.
After the death of Tycho Brahe, the German Johannes Kepler (1571-1630) gave him the continuation, on the one hand making other observations and on the other carrying out an exhaustive investigation of all the data taken. While Tycho developed a special planetary system in his day, Kepler was in favor of Copernicus. The aim of his works was to make them more accurate than the astronomical tables of the movements of the planets in that period. But I just wanted to adapt the heliocentric theory at the base, because for its harmony and simplicity, I saw it fascinated and at ease. From the beginning of his works, Pythagorean and Neoplatonic metaphysics had a great influence. This trend continued during the Renaissance challenging Aristotelian hegemony.
According to Kepler, the tendency of divine intelligence was somehow geometric and the characteristics of this order could be found in the mathematical relationships leading the heliocentric system. Therefore, in one of his first works he tried to relate the six planets known and their distances to the Sun with the five regular solids of geometry.
When he wanted to adapt the new data obtained from Martitz's orbit to the Copernic system and after four years of hard work, he came to a very important conclusion, which was impossible! The new data placed the orbit eight minutes from the Copernican scheme. Although Copernic in his day, knowing that the data used were not accurate, did not give importance to this difference, Kepler knew that Tycho's data were much more accurate than the aforementioned difference, so what was achieved was unacceptable. Therefore, and with the honesty that corresponds to scientists, there was no attempt to deny observations and invent new hypotheses to save the theory accepted by themselves. However, for him those eight minutes indicated: That the Copernic system was not able to express the actual movement of Mars. So he abandoned the Copernican system with its concentric spheres and epicycles.
For Kepler that would be very hard, because he was a supporter of the Copernican system. However, he went ahead and had to break the yoke linking the Copernican system with ancient Greece. When he studied the trajectories of the planets according to heliocentric theory, it occurred to him that the image of the paths could be of the ellipse (characteristics of the ellipse a. C.). II. They were known since the 19th century). If this was accepted, that is, that the natural path of a planet is ellipse, a geometric scheme of great ease was built for the world. In this scheme, all planets move in elliptical orbits, with the Sun in a focus. This law is one of Kepler's three main laws and is generally said to be the first.
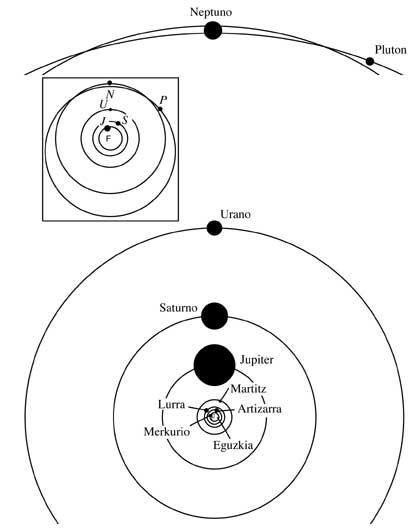
This first law of Kepler, in directing the heliocentric theory of Copernic, gives us a very simple image of the solar system. All epicycles and eccentrics of Copernic are ruled out: orbits are only ellipses. In the image you can see the current and simple scheme of the solar system
These ellipses are almost circles and all orbits are almost on the same plane, except for Pluto. This has a strong inclination and both in the image and in others, the orbits of Neptune and Pluto are not humiliated at any point in space.
Probably Kepler was happy to come to a conclusion as simple as this (after dispensing with the epicycles and eccentric that were very complicated), seeing that everything was done well through the ellipses. However, she herself had a concern: we can understand Plato's tendency to recognize that circular and uniform movements were natural, but why does Nature choose the ellipse? To answer this question correctly we must wait for the arrival of Newton, who told us that the law of ellipse is a consequence of another law of Nature much wider. So, let's leave the issue for now.
Therefore, we must think that Kepler's first law is a summary of the observations made, that is, an empirical law. But, although this law gives us an account of all the locations of a planet, it tells us nothing about when that planet will be in one place or another, that is, it tells us the image of the orbit, but its speed does not. Therefore, this law is very short because astronomers (and Kepler too) want to know beforehand when a planet will be at one point. Therefore, before his first law came out, Kepler had established a second law that indicates the changes in the speed of a planet.

Kepler knew that if there was a mathematical relationship between the speed of one position and another in the orbit of a planet, the system would be much simpler. If this relationship were discovered, the movement of a planet could be expressed with very little data. Two data were needed to provide the same ellipse, the third to reach speed at a specific point of travel (in perihelion, for example, the closest point to the Sun) and the other to know the inclination of the orbital plane to other planets. But no one knew that relationship. That's why, when he came up with this law it is said that he was in ecstasy, but what we know is that to find it he had to analyze a lot of data and perform a constant and hard work.
In any case, the path that followed to achieve this second law is surprising, since based on the three erroneous hypotheses came to its conclusion. In Kepler's words, the orbit describing the planets is due to the force exerted by the Sun and whose value was inversely proportional to the distance between the Sun and the planet. The speed and force that drives the planet were directly proportional to each other and therefore inversely proportional to the distance. This hypothesis (that is, that speed is proportional to force) is today unacceptable, but it can be seen as the idea of Aristotle or as something common sense gave at that time.
According to this hypothesis, the time it takes a planet to travel a small distance during the tour would be proportional to the distance to the Sun. This is almost entirely correct and so at some points in the orbit. Therefore, Kepler wanted to calculate the time needed to complete a large stretch of travel (and therefore when the distance to the Sun is variable). To do this, he took into account the distances of all the small arches that form this great stretch and concluded that this time is directly proportional to the surface that covers the line that goes from the Sun to the planet. According to this second law, the Earth (or if you want the Sun at the bottom of the stars) is understood to move faster in winter than in summer, something that both Kepler and his predecessors knew perfectly.
Both laws were published in 1609 in the book Astronomy Nova. But Kepler did not like and had a concern: no relationship was known between the movements of the different planets. Each planet moved in its ellipse and at its speed, but it seems there was no overall model for everyone. Kepler thought that this general model should exist, so there should be a relationship that relates all the movements present in the solar system. Kepler left behind this relationship and used music theory, according to the followers of Pythagoras, in search of a link between the orbits of the planets and musical notes. If his prolific work was called The Harmony of the World, he wanted to express something.
Believing in that relationship (or rather, its obsession) can, on the one hand, express the first magical faith of the numbers Kepler had, but also the tendency of all the geniuses of science. According to them, Nature is uniform and simple. This belief has given great help to scientists and a force to overcome obstacles. That is the case of Kepler, who after discovering his third law for having suffered a thousand personal misfortunes, was able to write:

... after having long found a real distance from orbits using Brahe's data, a real relationship... the fact that there is such a broad consensus between the work I present today and the work I have done for seventeen years on Brahe's observations, cleared my shadows from my mind and thought that at first it was in my dreams...
According to the current language of this law, if the period of a planet is T (i.e., the time of making a complete turn around the Sun) and R its mean radius, T 2 = K . R is 3, K being an equal constant for all planets. In the case of Earth T = 1 year and R = 15 x 10 7 km, so if we know your radius R for any other planet, we can find the period.
This third law is called harmonic law, because it represents a beautiful harmonic relationship between the planets.
Through all this, logically relating our solar system, we see it as a simple whole: our intelligence captures Kepler's universe with a glance and is able to mathematically express the laws that govern it.
Kepler, from Brahe's data, tried to construct detailed tables of planetary movements. To carry out this work he had to abandon some of the opinions accepted at that time. This attitude was completely new, that is, to give priority to observations, if they were carried out precisely and quantitatively. Another important aspect is the prediction of the use of mathematical language in the expression of physical laws. Later, the equations would be the natural expressions of the physical laws.
On the other hand, the movement of the planets in their orbit in the Kepler system was not considered to be produced by any god (as scholastics demonstrated), nor by their spherical forms represented circular movements. In his latest book ( Mysterium Cosmographicum) he tells us how he changed his views in 1596:

At one time he firmly believed that the force of a planet's movement was in a soul... However, when I thought that this cause of motion decreased with distance (i.e., as the light of the Sun decreases with distance to this star), I came to the conclusion that that force should be substantial, not literally, but… as we say that light is something substantial, that is, something non-spiritual and coming out of a substantial body.
In 1605 he wrote to a friend:
I have been very busy researching physical causes. My essay has consisted in demonstrating that the celestial machine must be compared to a divine organism and not to a work of watchmaking (and whoever believes that a watch has a soul, attributes honor to the watchmaker), and that in that watch all different movements are the result of a simple magnetic force, as all movements of the machine of a watch are the result of a single weight. Moreover, I demonstrate that this physical conception must be expressed by calculation and geometry.
In Kepler we can clearly see the change initiated in Europe two centuries earlier. Daily observation, the results, in short, give way to simple speculations and theories have to be based on that reality. That is why we can say that Kepler made a first claim to the modern attitude of science.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia






