Ultrafero esquecido ou a xente sabe quen é o momento lineal?

Hai magnitudes físicas moi coñecidas, como a velocidade, a forza, a potencia, o traballo, a enerxía… que son moi famosas e que son coñecidas non só polos científicos, senón por calquera outro.
Velocidade? Si, claro, indica a rapidez dos desprazamentos, en metros por segundo, ou en quilómetros por hora, paira medir os movementos dos automóbiles (e pór multas), etc.
Forza! Quen non coñece a forza? Os harrijasotzailes teñen algo terrible, os remeiros tamén actúan a lume de biqueira… a unidade de forza leva o nome do famoso Newton, aínda que é una combinación de unidades simples: kg·m/s2.
Potencia! Honorable… A magnitude sacra coa que valoramos aparellos e instrumentos! Os automóbiles necesitan o máximo posible, os aparellos domésticos tamén… A unidade é o watt (kg·m2/s3) e a unidade de potencia equina equivalente…
Traballo ou enerxía. Iso tamén é bastante prestixioso. Ás veces resulta algo confuso porque hai moitos tipos de enerxía: potencial, cinética...; todos os tipos de enerxía teñen a mesma unidade, outra denominación digna: o xullo (kg·m2/s2).
Algo máis escondido que esas magnitudes tan famosas, existe outra magnitude física, máis descoñecida que as mencionadas; non é famosa… case ninguén a menciona. Sempre se dedica a traballos ocultos. Sempre ás escuras e ninguén se dá conta diso. Con todo, é una magnitude física de gran importancia. Máis importante que case todos. Merece a pena ser citado e tratado con amabilidade.
Antigamente denominábaselle cantidade de movemento, pero na actualidade prevaleceu outro nome: momento lineal ou P. Multiplica a masa e a velocidade dos corpos: M·V. É un vector, é dicir, ten una dirección, a mesma dirección que a velocidade. A unidade do momento lineal (kg·m/s) nunca mereceu a pena, ao parecer, o nome dalgún físico recoñecido, xa que non ten nin nome curto nin nome, polo momento.Pois ben, o momento lineal goberna as interaccións entre os corpos. É dona de interaccións entre corpos. Eu diría Deus. Aínda que o corpo vaia, vinga, choce, parta, explota, pegue ou teña calquera tipo de interacción, o momento lineal mantense: P = cte. Non cambia de calquera xeito. Mantén o valor. Vale o mesmo si temos en conta todo o conxunto illado de todos os corpos que interveñen (o que se debe á lei de acción e reacción de Newton, segundo a cal se un corpo exerce una forza sobre outro, o outro exerce una forza do mesmo valor sobre o primeiro, pero en sentido contrario: SEMPRE).
Ten en conta que cando un corpo de calquera tipo atrae ou repele a outro, pase o que pase entre ambos, non conseguen cambiar o momento lineal total. Por exemplo:
Supoñamos que dous patinadores están xuntos, parados e de súpeto empúxanse uns a outros (dá igual que un empuxe ao outro, ou viceversa, ou ambos se empuxan mutuamente).
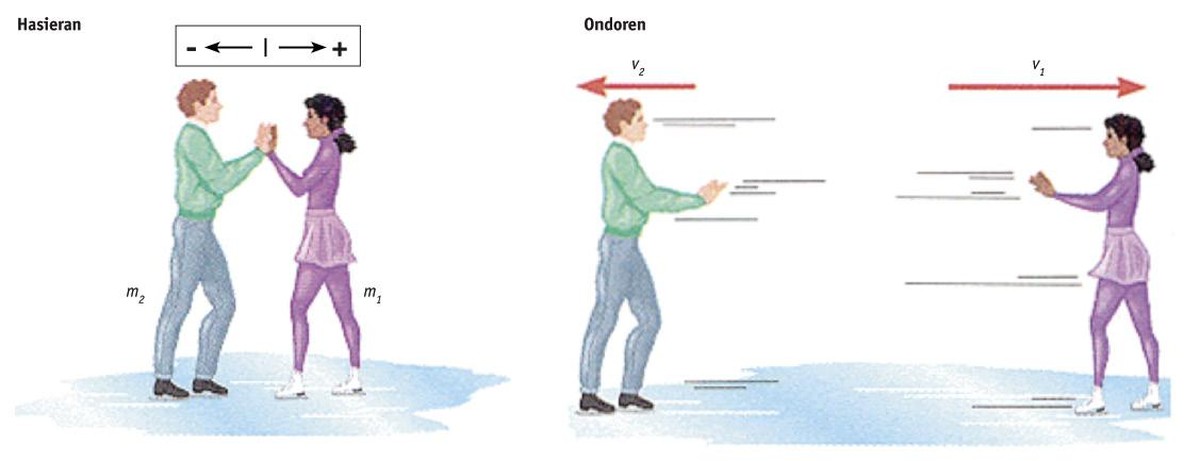
Anotemos o valor do momento lineal, o produto das masas e das velocidades:
Inicialmente (antes do empuxe), Phas= m1·0 + m2·0 = 0 é nulo porque os dous patinadores están parados.
A continuación, ?= m1·v1 + m2·v2
O momento lineal non cambia, polo que Phas= ? ou ben: 0 = m1·v1 + m2·v2;
Cun pouco de matemática elemental pódese escribir a seguinte expresión:
v2/v1 = - m1/m2
Por exemplo, se os dous patinadores teñen a mesma masa (m1 = m2) e un deles, por empuxe, toma una velocidade de 1 m/s, o outro alcanzará una velocidade de –1 m/s (igual valor pero en sentido contrario). Ou si una a 5 m/s, a outra a 5 m/s. Así mesmo, se un patinador ten a metade da masa (m1/m2 = 0,5), detectará o dobre de velocidade v1/v2 = 2. Sempre máis rápido (o menos masivo). En función da proporción das masas, as velocidades serán xustamente inversas.
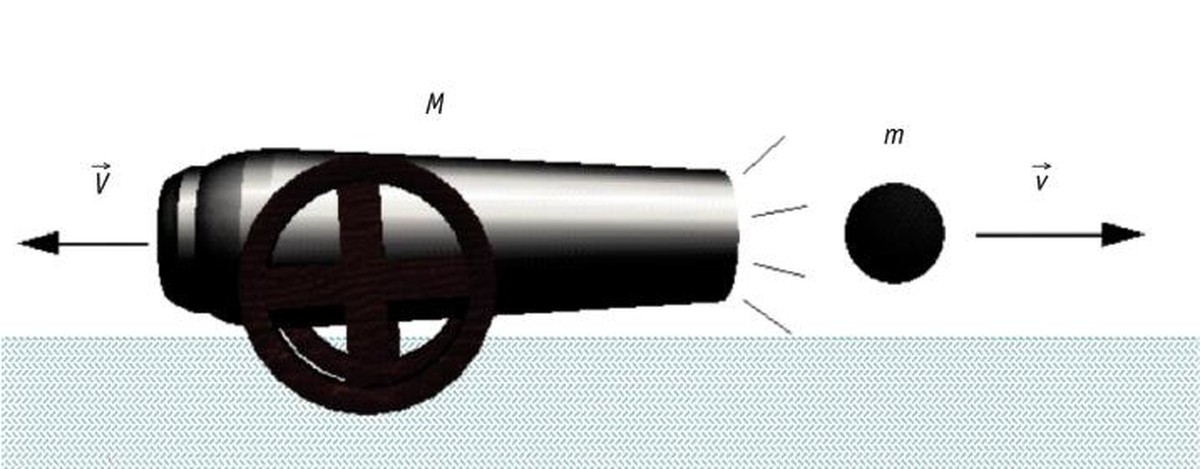
Por exemplo, cando una escopeta ou un canón disparan, se a relación de masas é M/m = 100 e sábese que a velocidade da bala é v = 100 m/s, a velocidade do canón cara atrás será: V = 1 m/s.Esta velocidade de retroceso do canón é inevitable porque o momento lineal así o establece a lei de acción e reacción de Newton; mesmo cando lancemos algo, o proxectil empuxaranos cara atrás.
Na mesma liña, supoñamos que dous coches chocan entre si e quedan pegados. Como saber cara a onde se moverán tras o choque? Aplicando de novo a conservación do momento lineal:
P antes = m1·v1 + m2·v2 Despois = m1·V + m2·V;
Se quedan adheridos, ambos terán a mesma velocidade (V).
Escribir despois Pllehen = P, de onde se pode calcular a velocidade V despois do choque:
m1 v1 + m2·v2 = (m1 + m2)·V; V = (m1v1 + m2·v2) / (m1 + m2)
Mesmo poden quedar paradas en determinadas condicións: a mesma masa e velocidades de igual valor (de sentido contrario), ou a dobre masa e a metade da velocidade, etc., podendo combinarse con condicións previas ao impacto.

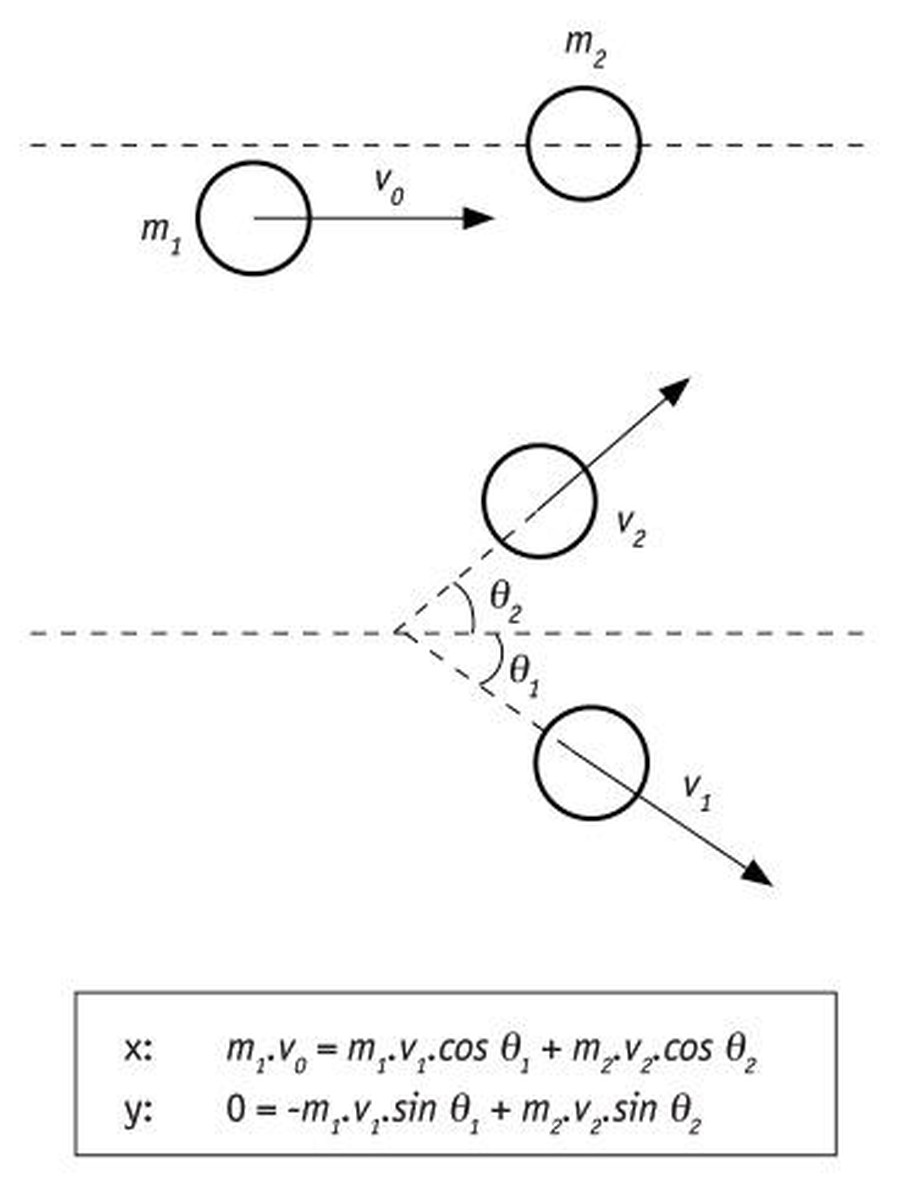
É máis, como o momento lineal ten carácter vectorial, tamén goberna os choques entre bólas de billar [1].

Este carácter vectorial analízase en dúas direccións convencionalmente (x e e) e estudando por separado as dúas proxeccións do momento lineal. Ser P constante significa que ambas as proxeccións deben ser constantes á vez:
Px= cte. e Py = cte.
No caso de patinadores, balas de canón, coches ou bólas de billar, só dous corpos participaron na interacción, pero poden existir máis corpos, e entón consérvase o momento lineal total, como os fogos artificiais. No momento da explosión, se o explosivo está parado, a suma dos momentos lineais de todas as partes (explosións simétricas) debe ser igual a cero.

Pola contra, se o artefacto estaba en movemento no momento da explosión, despois da explosión o momento lineal debe ser o mesmo entre todos os compartimentos, e non salgue a explosión simétrica, senón a dirección que levaba antes.
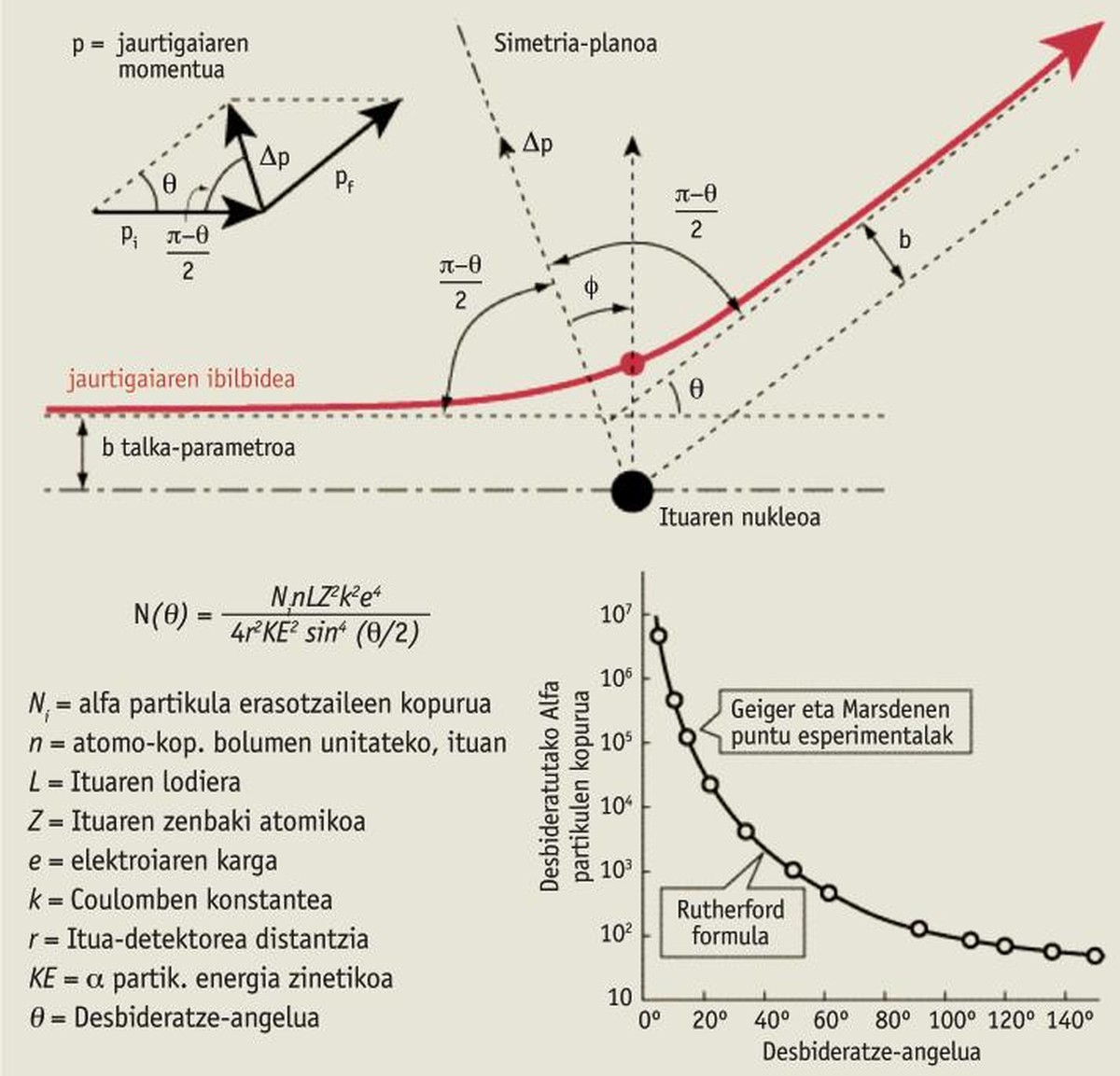
A capacidade do momento lineal abarca todos os ámbitos da física, desde o nivel microscópico até o nivel astronómico. Desde choques ou explosións entre asteroides e planetas até interátomos. Por exemplo, no intento de comprender e explicar a estrutura dos átomos, Ernest Rutherford descubriu o núcleo dos átomos en 1911 grazas á “conservación do momento lineal”.
Así, Rutherford descubriu os raios alfa na radiación emitida polos elementos radioactivos (carga eléctrica positiva e enerxía moi elevada), descubrindo posteriormente que son núcleos de helio, unidos a dous protones e dous neutróns, e, paira coñecer mellor estas partículas alfa, ocorréuselle lanzar una gama de raios alfa contra un fino papel de ouro. Así o prometeu a dous novos estudantes: Hans Geiger e Ernest Marsden. Esperaban que aquel poderoso raio atravesase de lado a lado aquel fino papel de ouro, aínda que quizais se desviase un pouco. O resultado foi sorprendente. Case todas as partículas alfa tiveron un percorrido correcto, tal e como se esperaba, pero algunhas delas desviáronse enormemente e outras mesmo rebotaron cara atrás! Sorprendente! “Lanza un canonazo contra unha fina capa de papel e rebota balas de canón! !” [2].
A explicación teórica de Rutherford e o exemplo das bólas de billar son moi similares, aplicando a conservación do momento lineal, e é perfectamente coherente cos resultados deste experimento (ver cadro adxunto).
As conclusións desta investigación revolucionaron a estrutura do átomo: os átomos deben ter un pequeno centro, o núcleo (uns 10-14 m). Este núcleo debe ter carga eléctrica positiva e case toda a masa do átomo, e ao seu ao redor, deixando case todo o espazo baleiro, os electróns deben estar [3]. Se non aplicase a conservación do momento lineal, non puidese obter tal efecto.
Ademais deste importante descubrimento do núcleo do átomo, a conservación do momento lineal ha traído consigo outros moitos descubrimentos.
O propio Rutherford postulou o neutrón en 1920 recollendo as masas e velocidades dos produtos que se producen nas desintegracións radioactivas, pero non atopou neutrón, xa que ao non ter carga eléctrica é difícil atopar a pegada de neutróns. Doce anos despois, en 1932, J. O físico inglés Chadwick descubriu experimentalmente estes neutróns. Sempre nos cálculos de desintegración tense en conta o momento lineal, como no caso dos patinadores [4].
En 1923, A. O estadounidense Compton demostrou que, ademais das partículas de materia, a radiación electromagnética tamén ten un momento lineal e serviu paira reforzar o modelo corpuscular dos fotóns creados nos últimos anos. A demostración teórica do efecto Compton utiliza tamén a conservación do momento lineal, como as bólas de billar [5].
Wolfgang Pauli utilizou tamén a conservación do momento lineal en 1930 paira postular a partícula denominada neutrino. E en 1956, C. Cowan e F. Foi descuberto por Reines [6].
Ao comezo deste artigo mencionei a lista das magnitudes físicas máis prestixiosas (velocidade, forza, potencia…). Non quixese quitar importancia, pero creo que na parte superior desa famosa lista habería que incluír outra magnitude: o momento lineal. Esta magnitude non é suficientemente coñecida (ultraprecisión esquecida) e, segundo vimos máis adiante, debería ocupar un lugar entre as magnitudes físicas máis prestixiosas.
Bibliografía
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian