Ultrafero oblidat o la gent sap qui és el moment lineal?

Hi ha magnituds físiques molt conegudes, com la velocitat, la força, la potència, el treball, l'energia… que són molt famoses i que són conegudes no sols pels científics, sinó per qualsevol altre.
Velocitat? Sí, clar, indica la rapidesa dels desplaçaments, en metres per segon, o en quilòmetres per hora, per a mesurar els moviments dels automòbils (i posar multes), etc.
Força! Qui no coneix la força? Els harrijasotzailes tenen una cosa terrible, els remers també actuen de gom a gom… la unitat de força porta el nom del famós Newton, encara que és una combinació d'unitats simples: kg·m/s2.
Potència! Honorable… La magnitud sagrada amb la qual valorem aparells i instruments! Els automòbils necessiten el màxim possible, els aparells domèstics també… La unitat és el watt (kg·m²/s3) i la unitat de potència equina equivalent…
Treball o energia. Això també és bastant prestigiós. A vegades resulta una mica confús perquè hi ha molts tipus d'energia: potencial, cinètica...; tots els tipus d'energia tenen la mateixa unitat, una altra denominació digna: el juliol (kg·m²/s2).
Una cosa més amagada que aquestes magnituds tan famoses, existeix una altra magnitud física, més desconeguda que les esmentades; no és famosa… gairebé ningú l'esmenta. Sempre es dedica a treballs ocults. Sempre a les fosques i ningú s'adona d'això. No obstant això, és una magnitud física de gran importància. Més important que gairebé tots. Val la pena ser citat i tractat amb amabilitat.
Antigament se'l denominava quantitat de moviment, però en l'actualitat ha prevalgut un altre nom: moment lineal o P. Multiplica la massa i la velocitat dels cossos: M·V. És un vector, és a dir, té una direcció, la mateixa direcció que la velocitat. La unitat del moment lineal (kg·m/s) mai ha valgut la pena, pel que sembla, el nom d'algun físic reconegut, ja que no té ni nom curt ni nom, de moment.Doncs bé, el moment lineal governa les interaccions entre els cossos. És propietària d'interaccions entre cossos. Jo diria Déu. Encara que el cos vagi, vingui, choce, parteixi, explota, pegui o tingui qualsevol tipus d'interacció, el moment lineal es manté: P = cte. No canvia de qualsevol manera. Manté el valor. Val el mateix si tenim en compte tot el conjunt aïllat de tots els cossos que intervenen (el que es deu a la llei d'acció i reacció de Newton, segons la qual si un cos exerceix una força sobre un altre, l'altre exerceix una força del mateix valor sobre el primer, però en sentit contrari: SEMPRE).
Tingues en compte que quan un cos de qualsevol tipus atreu o repel·leix a un altre, passi el que passi entre tots dos, no aconsegueixen canviar el moment lineal total. Per exemple:
Suposem que dos patinadors estan junts, aturats i de sobte s'empenyen els uns als altres (és igual que un embranzida a l'altre, o viceversa, o tots dos s'empenyen mútuament).
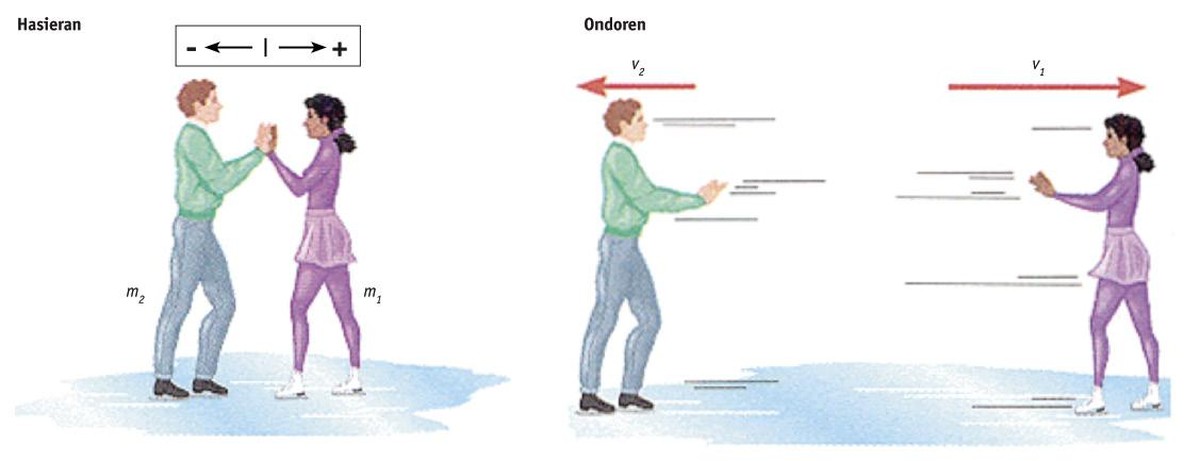
Anotem el valor del moment lineal, el producte de les masses i de les velocitats:
Inicialment (abans de l'embranzida), Phas= m1·0 + m²·0 = 0 és nul perquè els dos patinadors estan parats.
A continuació, ?= m1·v1 + m²·v2
El moment lineal no canvia, per la qual cosa Phas= ? o bé: 0 = m1·v1 + m²·v2;
Amb una mica de matemàtica elemental es pot escriure la següent expressió:
v2/v1 = - m1/m²
Per exemple, si els dos patinadors tenen la mateixa massa (m1 = m²) i un d'ells, per embranzida, presa una velocitat d'1 m/s, l'altre aconseguirà una velocitat de –1 m/s (igual valor però en sentit contrari). O si una a 5 m/s, l'altra a 5 m/s. Així mateix, si un patinador té la meitat de la massa (m1/m² = 0,5), detectarà el doble de velocitat v1/v2 = 2. Sempre més ràpid (el menys massiu). En funció de la proporció de les masses, les velocitats seran justament inverses.
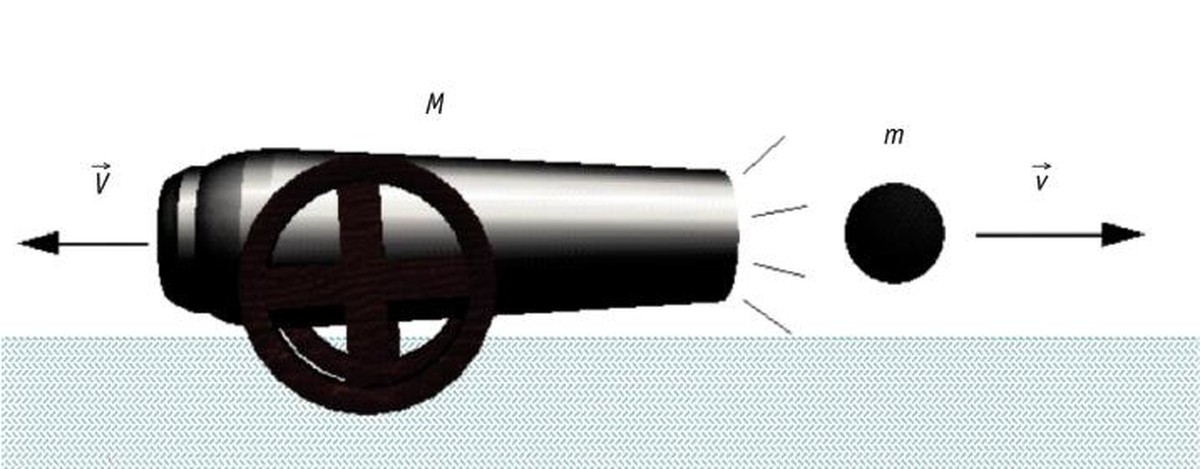
Per exemple, quan una escopeta o un canó disparen, si la relació de masses és M/m = 100 i se sap que la velocitat de la bala és v = 100 m/s, la velocitat del canó cap endarrere serà: V = 1 m/s.Aquesta velocitat de reculada del canó és inevitable perquè el moment lineal així ho estableix la llei d'acció i reacció de Newton; fins i tot quan llancem alguna cosa, el projectil ens empenyerà cap endarrere.
En la mateixa línia, suposem que dos cotxes xoquen entre si i queden pegats. Com saber cap a on es mouran després del xoc? Aplicant de nou la conservació del moment lineal:
P abans = m1·v1 + m²·v2 Després = m1·V + m²·V;
Si queden adherits, tots dos tindran la mateixa velocitat (V).
Escriure després Pllehen = P, d'on es pot calcular la velocitat V després del xoc:
m1 v1 + m²·v2 = (m1 + m²)·V; V = (m1v1 + m²·v2) / (m1 + m²)
Fins i tot poden quedar parades en determinades condicions: la mateixa massa i velocitats d'igual valor (de sentit contrari), o la doble massa i la meitat de la velocitat, etc., podent combinar-se amb condicions prèvies a l'impacte.

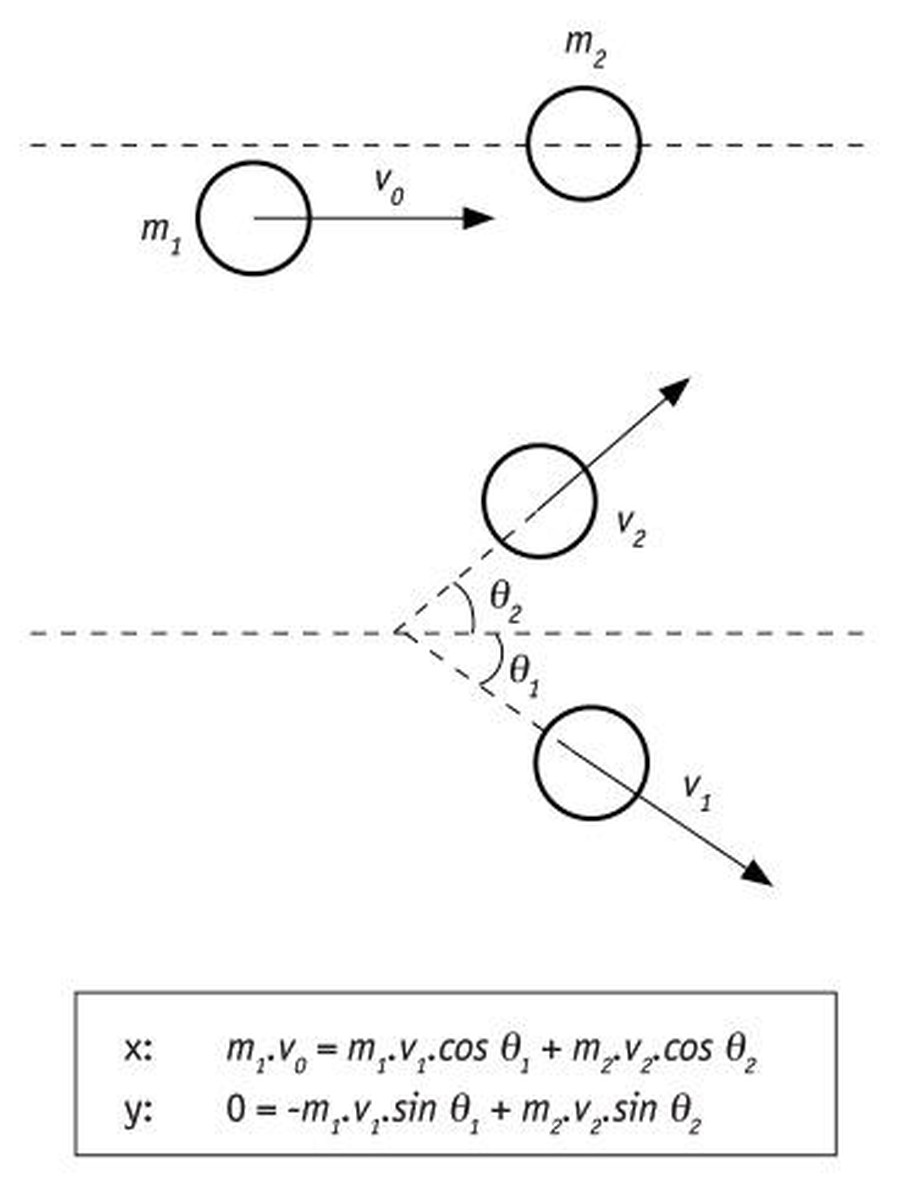
És més, com el moment lineal té caràcter vectorial, també governa els xocs entre boles de billar [1].

Aquest caràcter vectorial s'analitza en dues direccions convencionalment (x e i) i estudiant per separat les dues projeccions del moment lineal. Ser P constant significa que totes dues projeccions han de ser constants alhora:
Px= cte. i Py = cte.
En el cas de patinadors, bales de canó, cotxes o boles de billar, només dos cossos han participat en la interacció, però poden existir més cossos, i llavors es conserva el moment lineal total, com els focs artificials. En el moment de l'explosió, si l'explosiu està parat, la suma dels moments lineals de totes les parts (explosions simètriques) ha de ser igual a zero.

Per contra, si l'artefacte estava en moviment en el moment de l'explosió, després de l'explosió el moment lineal ha de ser el mateix entre tots els compartiments, i no surt l'explosió simètrica, sinó la direcció que portava abans.
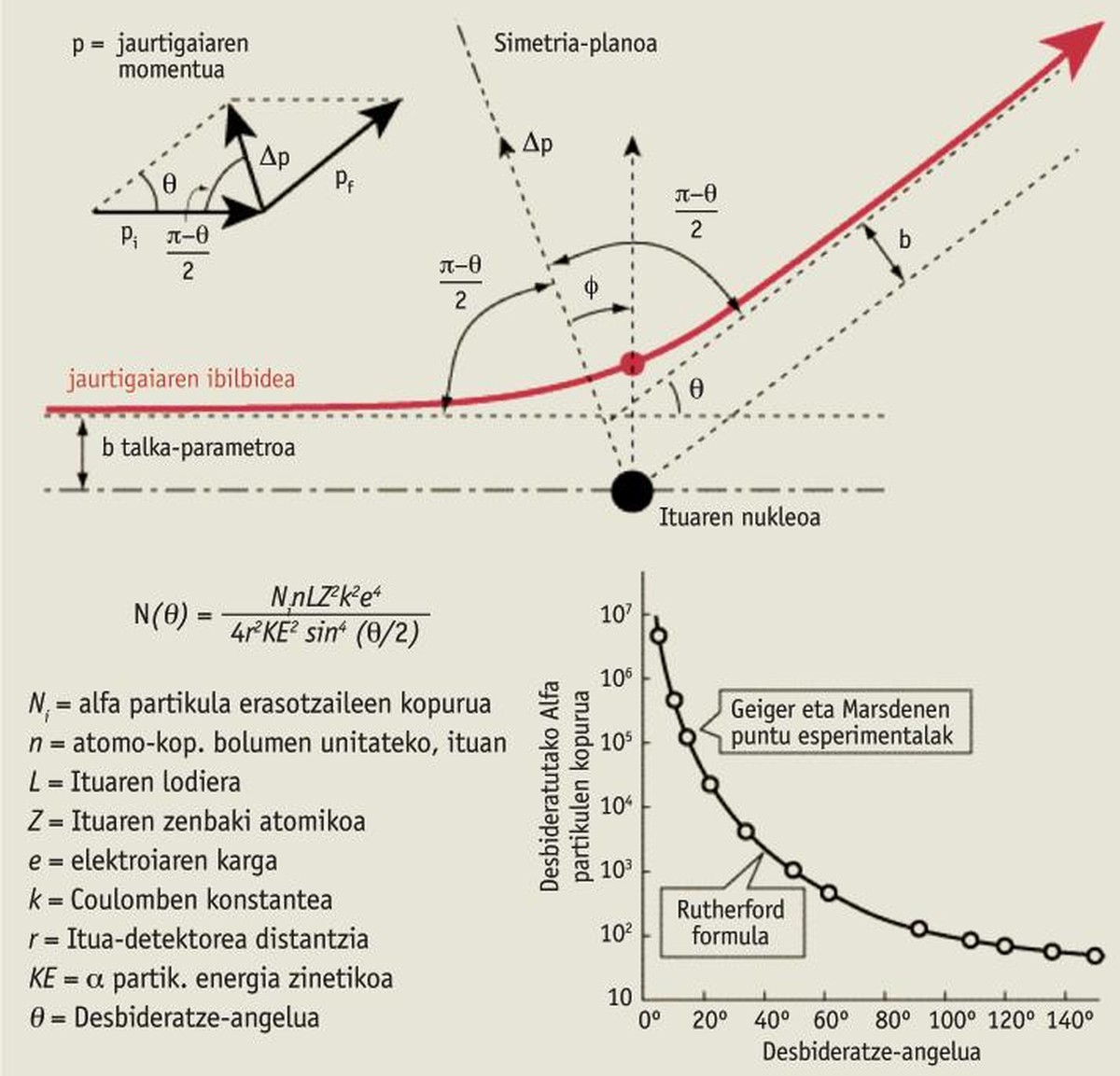
La capacitat del moment lineal abasta tots els àmbits de la física, des del nivell microscòpic fins al nivell astronòmic. Des de xocs o explosions entre asteroides i planetes fins a interátomos. Per exemple, en l'intent de comprendre i explicar l'estructura dels àtoms, Ernest Rutherford va descobrir el nucli dels àtoms en 1911 gràcies a la “conservació del moment lineal”.
Així, Rutherford va descobrir els raigs alfa en la radiació emesa pels elements radioactius (càrrega elèctrica positiva i energia molt elevada), descobrint posteriorment que són nuclis d'heli, units a dos protons i dos neutrons, i, per a conèixer millor aquestes partícules alfa, se li va ocórrer llançar una gamma de raigs alfa contra un fi paper d'or. Així ho va prometre a dos joves estudiants: Hans Geiger i Ernest Marsden. Esperaven que aquell poderós raig travessés de costat a costat aquell fi paper d'or, encara que potser es desviava una mica. El resultat va ser sorprenent. Gairebé totes les partícules alfa van tenir un recorregut correcte, tal com s'esperava, però algunes d'elles es van desviar enormement i unes altres fins i tot van rebotar cap endarrere! Sorprenent! “Llança una canonada contra una fina capa de paper i rebota bales de canó! !” [2].
L'explicació teòrica de Rutherford i l'exemple de les boles de billar són molt similars, aplicant la conservació del moment lineal, i és perfectament coherent amb els resultats d'aquest experiment (veure quadre adjunt).
Les conclusions d'aquesta recerca van revolucionar l'estructura de l'àtom: els àtoms han de tenir un petit centre, el nucli (uns 10-14 m). Aquest nucli ha de tenir càrrega elèctrica positiva i gairebé tota la massa de l'àtom, i al seu voltant, deixant gairebé tot l'espai buit, els electrons han d'estar [3]. Si no hagués aplicat la conservació del moment lineal, no hagués pogut obtenir tal efecte.
A més d'aquest important descobriment del nucli de l'àtom, la conservació del moment lineal ha portat aconsegueixo molts altres descobriments.
El propi Rutherford va postular el neutró en 1920 recollint les masses i velocitats dels productes que es produeixen en les desintegracions radioactives, però no va trobar neutró, ja que al no tenir càrrega elèctrica és difícil trobar la petjada de neutrons. Dotze anys després, en 1932, J. El físic anglès Chadwick va descobrir experimentalment aquests neutrons. Sempre en els càlculs de desintegració es té en compte el moment lineal, com en el cas dels patinadors [4].
En 1923, A. L'estatunidenc Compton va demostrar que, a més de les partícules de matèria, la radiació electromagnètica també té un moment lineal i va servir per a reforçar el model corpuscular dels fotons creats en els últims anys. La demostració teòrica de l'efecte Compton utilitza també la conservació del moment lineal, com les boles de billar [5].
Wolfgang Pauli va utilitzar també la conservació del moment lineal en 1930 per a postular la partícula denominada neutrí. I en 1956, C. Cowan i F. Va ser descobert per Reines [6].
Al començament d'aquest article he esmentat la llista de les magnituds físiques més prestigioses (velocitat, força, potència…). No voldria llevar importància, però crec que en la part superior d'aquesta famosa llista caldria incloure una altra magnitud: el moment lineal. Aquesta magnitud no és prou coneguda (ultraprecisión oblidada) i, segons hem vist més endavant, hauria d'ocupar un lloc entre les magnituds físiques més prestigioses.
Bibliografia
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian