Nikolai I. Lobatxevski (1792-1856): Des del no-res el nou món

1993/03/01 Duoandikoetxea Zuazo, Javier - EHUko matematika irakaslea Iturria: Elhuyar aldizkaria

• Matematika
• Historia

Poques vegades en la història de les matemàtiques hi ha hagut alguna cosa semblança a l'agreujat pel descobriment de la Geometria no euclidiana. Establia una crisi en les bases, però, com és costum, va sortir reforçat de la crisi, de tal manera que partia de les noves vies. Com a creadors de la geometria no euclidiana se citen principalment dos noms: El rus Nikolai Lobatxevski i l'hongarès János Bolyai. L'any 1992 que ens ha anat entre les celebracions dels famosos segles ens ha deixat ocults a uns altres, i un d'ells és el segon del naixement de Lobatxevski.

Euclides i cinquè postulat

En el segle tercer a. C. els grecs ens van oferir el primer llibre per a la història de les matemàtiques: Elements d'Euclides d'Alexandria. En ell s'analitzen els números i la geometria. A més del tema, l'important és el mètode, on es troba la base del mètode axiomàtic deductiu utilitzat en Matemàtiques. En primer lloc, hi ha afirmacions (postulats o axiomes) que no han de ser acceptades i provades prèviament. Posteriorment, aplicant les regles de la Lògica es proven altres afirmacions (proposicions o teoremes).

Quines condicions cal exigir als postulats quan es vol construir una teoria? D'una banda, és necessari que no siguin contradictoris (és a dir, que no es derivi un resultat ni el contrari). D'altra banda, convé no ser massa, encara que això no arruïnaria la teoria. Quan són massa? Quan un postulat és conseqüència d'uns altres, pot ser eliminat de la llista de postulats i aparèixer com a teorema, quedant tota la teoria sense modificar.

Euklides va utilitzar cinc postulats especials per a la Geometria. Encara que la formulació dels elements és més geomètrica, en paraules planes es poden definir com:

1. Per qualsevol dels dos punts es passa una sola recta.
2. Daus dos de manera directa, al costat del primer es pot col·locar un altre congruent amb el segon per a donar-li una recta més llarga.
3. Daus dos punts diferents, sempre hi ha una circumferència que té com a centre el primer i passa pel segon.
4. Tots els angles rectes són congruents.
5. Si una recta curta altres dues rectes i la suma dels angles interiors d'un costat és menor que dos rectangulars, s'uneixen estenent les rectes a aquest costat.

A pesar que els quatre primers postulats semblen acceptar-se sense dubtes, des de fa molt temps es va percebre que el cinquè és especial. En el treball d'Euklides també s'aprecia alguna cosa semblança a això (ja que va provar les 28 primeres proposicions sense utilitzar aquest postulat i només el va introduir quan li va resultar imprescindible).

En segles posteriors, molts matemàtics s'han preocupat pel cinquè postulat i es poden fixar dues posicions: algunes, que no van agradar molt la formulació d'Euklides i que la van substituir per una altra formulació més “acceptable”. Uns altres van intentar demostrar que el cinquè postulat era conseqüència d'altres quatre. Molts d'ells van donar la “demostració”, però sempre de manera involuntària, amb un postulat alternatiu. En els llibres i cursos habituals de la geometria euclidiana, un dels postulats alternatius va ocupar el lloc del que Euklides va donar: Des d'un punt exterior d'una recta es pot realitzar una única recta paral·lela. Per aquesta raó es diu al cinquè postulat de paral·lels.

Una manera de veure que el cinquè postulat (en qualsevol de les seves formulacions) és conseqüència de les anteriors és portar-lo a l'absurd: considerant que és cert el contrari, arribar a una contradicció. XIX. Abans del segle XX, els més avançats en aquest camí van ser el jesuïta italià Gerolamo Saccheri (1677-1733) i el suís Johann Heinrich Lambert (1728-1777). Saccherik va trobar resultats interessants però d'aparença bastant estranya (Per descomptat, comparant les geometries euclidià amb les quals estem acostumats).

Un d'ells va ser considerat impossible i amb això va arribar a la conclusió que el postulat dels paral·lels és correcte, tal com ens va ensenyar en el llibre Euklides garbi de tots els errors. Lambert va destacar, entre altres coses, que Saccheri no va arribar a contradicció i que va aconseguir més resultats per part seva. A més, va percebre que el cinquè postulat no es podia aconseguir com a conseqüència dels altres i que els resultats del contrari poden ser estranys des de l'experiència habitual, però en cap cas contradictoris des del punt de vista de la Lògica. L'única raó per a acceptar el postulat dels paral·lels seria, per tant, la conveniència. Gràcies a això, Lambert va ser pioner d'obres del segle següent.

XVIII. A la fi del segle XX, per part seva, l'opinió del famós filòsof Kant també va tenir una gran influència en el debat. Per a Kant no es pot inventar una Geometria diferent a l'euclidiana, ja que és un coneixement que tenim per endavant (a priori).

Aportació de Lobatxevski

Igual que molts altres, Lobatxevski va fer els seus primers passos per a demostrar el postulat dels paral·lels i va pensar que el va aconseguir. No va trigar a prendre un altre camí. El cinquè postulat deia que l'experiència “provava” i que no es pot donar una demostració fora d'ella, o que no es deu als quatre primers postulats. És més, la substitució d'altres quatre postulats per un altre postulat (no equivalent) i la construcció d'una Geometria diferent a l'euclidiana, també sense contradiccions. Malgrat la línia de Lambert que hem esmentat anteriorment, sembla que Lobatxevski no coneixia les seves obres.

El postulat alternatiu que va proposar era: des d'un punt exterior d'una recta es poden fer dues rectes diferents que s'uneixen amb l'anterior. “Les superfícies i les línies no estan en la Naturalesa, sinó en la imaginació”, dirà clarament, deixant la Geometria al marge del món físic (una altra cosa és la que millor s'adapti a les necessitats de la Física). Al principi va nomenar verbalment la Geometria imaginària i, posteriorment, la Pangeometría. Actualment es diu Geometria hiperbòlica (a vegades també Geometria de Lobatxevski). Els teoremes que es demostren en aquesta geometria, com s'ha esmentat anteriorment, no són habituals. Heus aquí un parell d'exemples:

• La suma dels angles d'un triangle és menor que dos rectangles i la seva superfície és proporcional a la qual falta perquè aquesta suma sigui dos rectangles.
• Si els angles de dos triangles són iguals, els triangles són iguals.

Lobatxevski va construir també la Trigonometria corresponent a aquesta Geometria, també diferent de l'habitual. Però hi ha relacions entre ambdues que se secunden entre si, és a dir, si una és possible, l'altra també.

Malgrat treballar en altres camps, Lobatxevski és conegut per Geometria. Al febrer de 1826 va parlar per primera vegada al públic de les seves noves idees i en 1829 va publicar aquest primer tema en el Butlletí de Kazan. Després van venir uns altres, sempre en rus, fins que en 1837 va treure una obra en francès en el famós Journal de Crelle (sota el títol de Geometria Imaginària) i tres anys després una monografia en alemany (Estudis Geomètrics sobre la Teoria dels Paral·lels). Un any abans de la seva mort va publicar una explicació completa sobre el títol Pangeometría, tant en rus com en francès.

Bolyai i Gauss

Lobatxevski no va ser l'única que va arribar a aquestes conclusions. L'obra “Ciència de l'Espai Absolut” que l'hongarès János Bolyai (1802-1860) va dedicar al seu pare, Wolfgang Bolyaire, a la Juventutem Studiosam in Elementa Mathesis (1832-33) similar a la de Lobatxevski. Quan el jove Bolyai en 1823 va informar el seu pare dels seus treballs, li va dir en una carta: “He fet descobriments tan fascinants que jo també he perdut la sorpresa: del no-res he creat un món nou diferent”. Era amic de Wolfgang Bolyai Gauss i en aquella època era el matemàtic més famós. Per això li va enviar el treball del seu fill perquè li donés la seva opinió.

La resposta de Gauss és: “Si em poso a dir que no puc elogiar aquest treball, et sorprendràs, però no puc fer una altra cosa, perquè m'elogiaria, perquè tot el contingut del treball, el camí que ha pres el teu fill i els resultats que vol aconseguir són gairebé íntegrament els reflexions que he realitzat en els últims 30-35 anys”. El jove Bolyai es va fer mal escoltant aquestes paraules, esperant que Gauss li volgués robar els seus resultats. D'altra banda, malgrat l'obra de Lobatxevski, al principi creu que estava copiada de la seva obra. Com a conseqüència, va abandonar definitivament les Matemàtiques. Però no és tan estrany obtenir resultats similars d'investigadors diferents sense copiar. Són molt il·lustratives les següents paraules de Wolfgang Bolyaire: “Sembla que a algunes conseqüències es pot arribar des de molts llocs, on es troben en diferents llocs (com va ocórrer), tal com apareixen les violetes a la primavera”.

El treball de Gauss amb Geometries no euclídicas no es coneix bé, ja que sembla que la reacció contra els filòsofs kantians no es va atrevir a acomiadar. Segons alguns autors, els resultats de Lobatxevski i Bolyaire es basen en idees preses indirectament de Gauss i hauríem de considerar a Gauss com el veritable creador de la Geometria no euclidiana. Uns altres, no obstant això, no ho accepten i afirmen que Gauss mai va ser a partir dels primers passos i que cal confessar-los el que li correspon a Lobatxevski i a Bolyai. En qualsevol cas, sembla que Gauss es va alegrar en treure al carrer l'obra dels altres, com després va enaltir l'aportació de Riemann en temes similars. A més, el nomenament de Lobatxevski com a membre de la Societat de Ciències de Göttingen (1842) va ser una proposta de Gauss.

Models euclidià

La renovació de la geometria no euclidiana en la comunitat matemàtica no es va notar ràpidament. Per a això van ser necessaris anys i, sobretot, l'aportació del matemàtic italià Eugenio Beltrami (1835-1900) li va donar el seu lloc en Matemàtiques. El fet de no trobar contradiccions en lloc del postulat dels paral·lels, no assegurava que no existís, ja que és impossible escriure tots els teoremes que es poguessin deduir. Però Beltrami va descobrir en el si de la Geometria euclidiana un model que compleix els requisits de la Geometria hiperbòlica i viceversa. En conseqüència, la Geometria euclidiana i hiperbòlica són totes dues possibles o totes dues impossibles. Va deixar totalment anul·lada la tendència a considerar la Geometria euclidiana com una “veritat”.

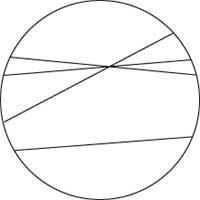
El model Beltrami-Klein (sense entrar en els detalls) és una cosa així: dins d'un cercle les rectes són normals (per descomptat, les parts que estan dins del cercle), però la manera de mesurar les distàncies canvia i també la de mesurar angles. Les “longituds” augmenten a mesura que s'aproximen al límit del cercle i, en realitat, la longitud d'una corda del cercle és infinita. És fàcil observar que en aquest cas el postulat euclidià dels paral·lels no es compleix. En aquest model Poincaré va proposar un canvi. Són rectes, diàmetres i trossos de circumferència (units a la circumferència que és el límit del cercle) i els angles es mesuren de manera normal, però no les distàncies.

Diguem, finalment, que a diferència de la Física newtoniana, la Física moderna utilitza models no euclidià per a descriure l'espai. El lector interessat per l'evolució de la geometria no euclidiana i els seus models euclidià en la revista “Elhuyar” J. Llombart, A. Bernalte i M. Pot veure els següents articles d'Ensunza: Esborrany històric de geometria no euclidiana, tom 11, vol. 2 (1985), pàg. 263-271. i models euclítricos del pla hiperbòlic, tom 12, vol. 2 (1986), pàg. 1-3.

Breu ressenya biogràfica Nikolai Ivanovitx Lobatxevski va néixer l'1 de desembre de 1792 a la ciutat de Nizhniy-Novgorod (durant diversos anys anomenada ciutat de Gorki). Encara que també s'ha esmentat una altra data de naixement, les recerques dels historiadors russos ho donen com a veritable. No obstant això, aquell dia era el 20 de novembre perquè no s'havia aprovat la reforma del calendari gregorià. Sent un nen de cinc anys, el seu pare va abandonar a la seva família i la seva mare va tornar a casa dels seus avis amb els seus fills. Va estudiar en el liceu de Kanzán i en 1807 va ingressar en la Universitat de Kazan, fundada dos anys abans. En 1811 va acabar els seus estudis obtenint el títol de Magister i allí li van proposar quedar-se com a professor. En 1816 va ser nomenat Catedràtic Especial i aquest mateix any va quedar l'escrivà del curs de Geometria. En ell no apareixen les idees que després va desenvolupar. En 1819 rep l'ordre de reorganització de les biblioteques i en 1820 és nomenat per primera vegada degà de la Facultat de Física i Matemàtiques. Va ser catedràtic en 1822, des de 1825 fins a 1835. Va ser director de la biblioteca i rector de la Universitat des de 1827 fins a 1846. En 1842 va ser nomenat membre de la Societat de Ciències de Göttingen. En 1846, si per primera vegada fos nomenat catedràtic, van passar 30 anys i havia de jubilar-se per llei. Com fins llavors només tenia 53 anys, van intentar obtenir l'exempció, però no va ser possible i va ser nomenat Representant del Secretari del Districte Acadèmic de Kazán. En teoria era un lloc important, però per a ell era totalment burocràtic i banal. Va abandonar el lloc en 1853 i va morir el 23 de febrer de 1856.