Mélange III

1991/12/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Les vacances de Noël nous permettent de profiter de ce petit repos que nous méritons. Cependant, notre habitude de travailler ne nous laisse pas la tête tranquille et nous faisons souvent un travail pour la maison. Pour ne pas passer cela, nous vous offrons 25 questionnaires pour vous divertir dans ces jours prestigieux.

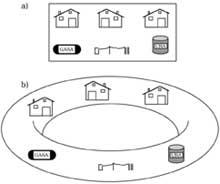
1. Voici trois maisons et réservoirs d'eau, de lumière et de gaz situés sur le plan (a). Les quartiers veulent relier leurs maisons aux gardes, mais sans traverser les tuyaux. Les aiderait-il ?

Dans la partie inférieure (b), les maisons et les gardes se trouvent sur un plancher à vis. Les quartiers ont le même problème. Allez-vous obtenir la solution?

2. Vous devez former une image de huit poxpoles avec quatre triangles et deux carrés.

3. Il faut effectuer quatre coupes droites à un carré. Avec les pièces obtenues, vous devrez compléter cinq carrés identiques.

4º Recadrez l'image latérale en deux parties égales.

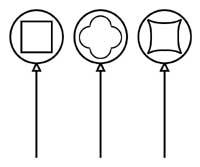
5. Si vous dessinez un carré dans le ballon vidé, quel aspect aura après avoir gonflé le ballon ?

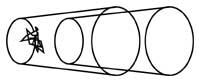
6º Comment tireriez-vous le papier sans toucher les forêts?

7. Un homme arrive chez lui la nuit. Bientôt, il réalise quelque chose et se suicide en prenant le pistolet. Mais s'il avait vu de la sciure sur le sol de sa maison, il ne serait pas tué. Quelle est la cause de ce comportement étrange?

8º. Supposons que quelqu'un a multiplié tous les premiers numéros (bien sûr ceux qui sont connus). Si le produit est L:

• Quel est le dernier chiffre de L ?
• le dernier chiffre est impair ou pair?

9. Trois frères ment trois jours par semaine, et dans d'autres cas disent la vérité. Le chef se trouve les lundis, mardis et mercredis. Ceux du centre les mercredis, jeudis et vendredis. Les plus jeunes les vendredis, samedis et dimanches. Les trois frères, réunis à Loyola, dirent:

Nerea: aujourd'hui vendredi est Josune: hier jeudi était Gorka: Josune est la principale

Quel jour de la semaine a eu lieu cette entrevue? Comment s'appellent les aînés, les médias et les plus jeunes ?

10. Tout comme laissant le nombre de poxpolos sur les deux côtés du symbole, comment faire l'égalité?

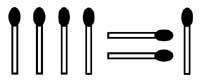
11. D’un côté d’une carte on peut lire la phrase “sur cette carte il y a deux affirmations”. De l’autre côté, la phrase “ce qui est dit derrière n’est pas vrai”. Quel est le mensonge?

12. Dans deux forêts, nous avons l'eau et le vin, la même quantité. De l'eau cinq gouttes sont prises et ajoutées au vin. Après avoir secoué cette forêt, on prend cinq gouttes qui sont laissées dans la forêt d'eau. Y a-t-il plus d'eau dans le vin qui est venu ? Ou l'inverse ?

13. Au total, sept sultans ont 2.879 femmes. Il n'y a pas d'égale quantité. Si nous divisons le nombre de femmes de n'importe quelle rangée par le nombre d'autres, nous obtiendrons toujours le nombre entier.

Dis donc Allah, combien de femmes il y a dans chaque parti.

14. Je suis monté à une cerise qui a eu la cerise.

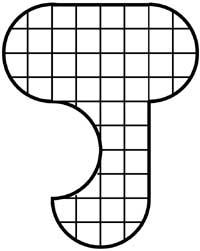
Je n'ai pas mangé des cerises, mais je l'ai laissée sans cerises.

Combien de cerises avait-il sur l'arbre?

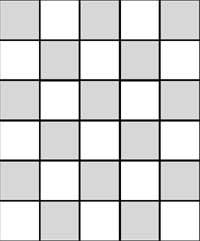
15. Avec les pièces suivantes, vous devez compléter le tableau d'échecs. Les pièces peuvent être tournées dans le plan, mais pas dans l'espace.

16. Un problème d'échecs consiste à placer sur un tableau des grilles 5x6 au roi, la dame, deux tours, deux alfiles (en différentes couleurs) et deux chevaux sans les attaquer.

Vous pouvez entrer une difficulté. Un pion sera placé dans les mêmes conditions, mais pas dans la première et dernière rangée.

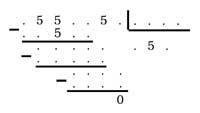
17. Voici une division dans laquelle on ne voit que 5 et 0. Vous devez remplacer les points par des nombres pour connaître la division.

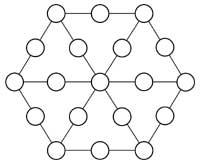
18. Placez les nombres de 1 à 12 en cercles blancs pour que les sommes des six nombres des cerceaux soient identiques.

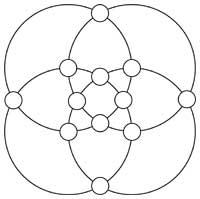
19. Maintenant similaire, mais cette fois avec des nombres de 1 à 19, pour que la somme sur les lignes de trois cercles (y compris les rayons) soit 22. Une fois cela accompli, replacez les nombres pour que la somme soit 23.

20. Il y a trois cartes face cachée. Nous savons qu'à droite d'un 1 il y a 2 ou 2 ; à gauche d'un 2 il y a 2 ou 2 ; à gauche d'une coupe il y a une ou deux épées et enfin à droite d'une épée il y a une ou deux épées. Quelles sont les trois cartes ?

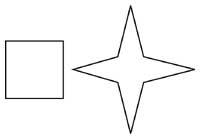
21. Avec quatre sections adaptées au carré adjacent, vous pouvez obtenir une étoile à quatre sommets.

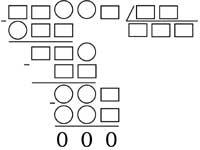
22. Sur l'image, vous pouvez voir un rectangle formé de carreaux en forme de L. Ce rectangle a une fente qui divise en deux rectangles. Le plus petit rectangle qui peut être fait sans rainures avec carreau en forme de L est la moitié de la figure. Mais quel est le prochain?

23. Une autre division. Dans elle les nombres impairs sont représentés par des carrés et des paires par des cercles. C'est une division exacte.

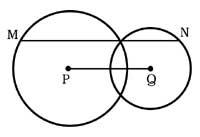
24. Les centres des circonférences de la figure se trouvent aux points P et Q, la longueur du segment PQ étant de 3 cm. Quelle est la longueur du segment MN qui passe par un point de coupe et parallèle au PQ ?

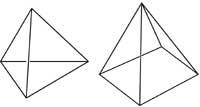
25. Voici deux pyramides. Aux deux extrémités, les longueurs sont égales. Quels sont les volumes des pyramides ? (sans calcul).

Si vous avez un écart entre les femmes pour essayer de répondre à ces questions, merci beaucoup. Vous avez certainement réussi et vous n'aurez pas à demander des réponses. Cependant, si vous ne l'avez pas essayé (vous êtes toujours à l'heure) ou si, même si vous l'avez essayé, vous n'avez pas trouvé toutes les réponses, vous voudriez que vous le fassiez pour les vérifier ou pour connaître celles que vous n'avez pas trouvées. Dans ce cas, veuillez nous informer et nous vous indiquons que vous recevrez la réponse appropriée.