Matematika, hezkuntza eta generoa gurutzatzen diren lekuen kartografia bat

Zein neurritan dago zientziaren izaera maskulinitatearen ideiari lotuta? Galdera hori bota zuen Evelyn Fox Keller fisikari eta epistemologo feministak 80ko hamarkadan, Reflections on gender and science liburuan. Galderari erantzuteko, ezagutza zientifikoa ezaugarritzeko modu historiko batzuk aztertu zituen. Francis Baconen obraren bitartez, adibidez, erakutsi zuen genero-rolek eta estereotipoek eragin nabarmena izan dutela garaian garaiko zientzia ezaugarritzeko moduetan. Izan ere, Baconek adimena maskulinotzat zuen, eta natura femeninotzat; ezagutza zientifikoa adimenak natura menderatzean datzala esan zuen, eta adimenaren eta naturaren arteko harremana ezkontza heterosexual batekin parekatu zuen. Rene Descartesen pentsamenduaren analisiak, aldiz, balio izan zion ikusteko zientzia ezaugarritzeko moduek, orobat, inpaktua izaten dutela genero-sistemetan. Gizakia bi zati disjuntuk osatzen dutela baieztatu zuen Descartesek: adimenak eta gorputzak. Adimen-gorputz dikotomiaren ondorioz, maskulinitatearen eta feminitatearen estereotipo askoz muturrekoagoak garatu ziren, maskulinitatea adimenarekin lotu baitzen eta, feminitatea, berriz, gorputzarekin eta, batez ere, umetokiarekin. Horrek lanaren banaketa sexuala ekarri zuen, emakumeak eremu erreproduktibora zokoratu zituena.

Beste epistemologo feminista askok ere agerian utzi dute ikerketa zientifikoaren izaera ez-neutral, androzentriko eta sexista. Matematikaren baitako genero-dinamikak azaleratzeko ahaleginak, baina, dezente apalagoak izan dira. Arrazoiak hainbat izan daitezkeen arren, matematikaren abstrakzio-maila altua da, ziur asko, nabarmenetako bat, izaera abstraktu horrek pribilegiozko posizioa eman baitio bai ezagutza-eremuari, bai egia matematikoari. Hutsune hori betetzen laguntzeko asmoz, matematika-­hezkuntzan generoak hartzen dituen formetan arakatu dut tesian, matematikarien, matematika-­irakasleen eta matematika-ikasleen bizipenak, diskurtsoak eta ekintzak oinarri hartuta. 

Iparrorratz eta koordenatu metodologikoak

Tesia kasu-azterketa bat da. Matematika, hezkuntza eta generoa egunerokotasunean zer baldintzatan gurutzatzen diren aztertu dut bertan, ikasgela agertoki behinentzat hartuta. Helburua kasuaren partikulartasuna, bakartasuna eta konplexutasuna zehatz aztertzea izan arren, ikergaiaren inguruko baieztapen orokorragoak ere egin ditut, ikerketaren izaera instrumentalari jarraikiz. Horrelakoetan, ohikoa da kasu bakarraren azterketak fenomeno orokorrago bati buruzko baieztapenak egiteko zabaltzen dituen aukeren inguruan zalantzak agertzea, diseinu kuantitatiboetan erabiltzen diren baliabide estatistikoak falta direlako. Hala ere, badaude ikerketaren baliotasuna indartzeko bestelako moduak, diseinu kualitatiboei hobeto egokitzen zaizkienak.

Horietako bat triangulazioa da, analisi gurutzatua egiteko modu bat, gaiak kontrastatzea eta angelu desberdinetatik aztertzea ahalbidetzeko, baita baieztapen garrantzitsuenen atzean dauden ebidentziak sendotzeko ere. Bi triangulazio-mota erabili ditut tesian: datuen triangulazioa eta triangulazio metodologikoa. Datuen triangulazioari dagokionez, hainbat informazio-iturritara jo dut, matematika-ikasleek zein -irakasleek parte hartu baitute ikerketan. Triangulazio metodologikoari dagokionez, askotariko teknikak eta erremintak erabili ditut informazioa ekoizteko: sakoneko elkarrizketak eta galdetegi ireki, itxi zein mistoak, besteak beste. Gainera, 200 ordu baino gehiagoko behaketa egin dut hiru matematika-­ikasgelatan. Parte-hartzaileen baliozkotzea ere bilatu dut, haien hitzei emandako esanahiekin ados daudela egiaztatzeko. Azkenik, teoriaz baliatu naiz prozesu analitikoan ekoitzitako ideietan sakontzeko, istorioak kontzeptualizatzeko eta nire interpretazioei indarra emateko.

Hala, matematika, hezkuntza eta generoa gurutzatzen diren leku batzuen berri ematen duen kartografia bat osatu dut, orainean endredatutako interpretazio bat, partziala eta bukatugabea. Leku horiek ezagutarazteko lau ibilbide zirriborratu ditut (1. irudia), eta datozen lerroetan laburbildu.

1. irudia. Tesiaren azaleko irudiko kartografian, testura-mota bakoitzak ibilbide bat sinbolizatzen du. Arg. M. Altuna, U. Albizu-Mallea

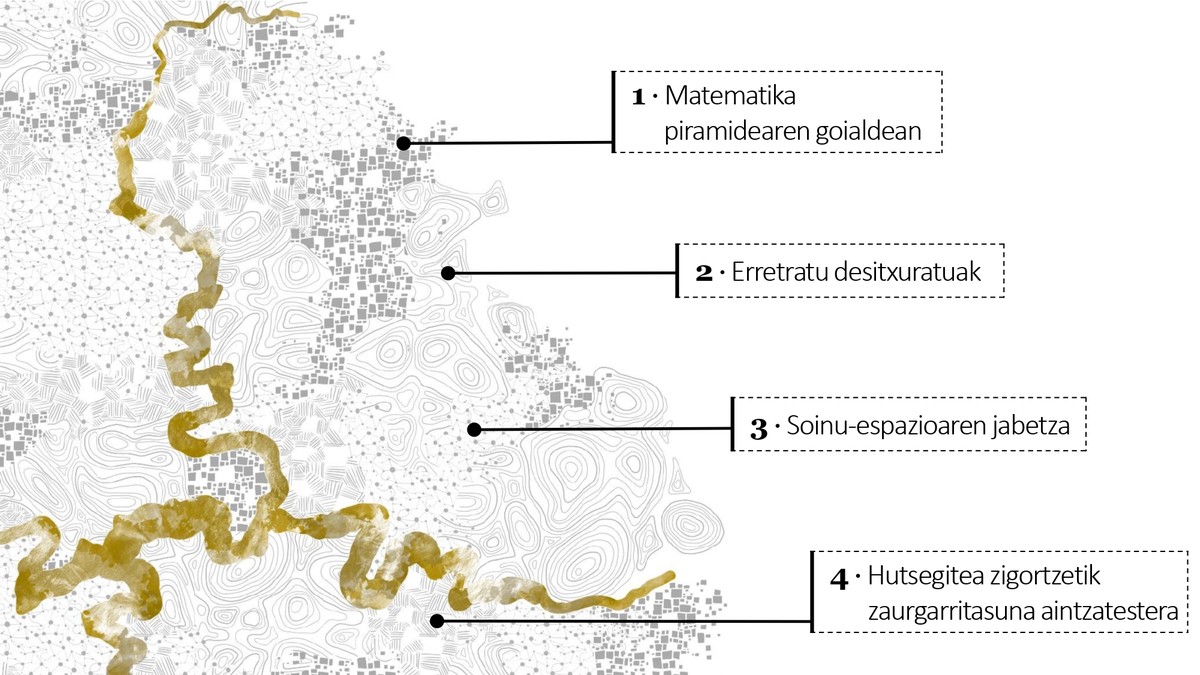
Lehenengo ibilbidea: matematika piramidearen goialdean

Azken mendean, matematika nazioen interesak defendatzeko bitarteko behinenetako bat bilakatu da. Bigarren Mundu Gerraz geroztik, zientzialari, teknologo, ingeniari eta matematikarien kopurua areagotzea ekonomia eta segurtasun nazionala indartzearekin lotzen da. Aurkikuntza zientifikoen eta berrikuntza teknologikoen abangoardian egoteko ekite horren atzean, aurrerabidearen ikuskera modernoa dago, zeinak garapen zientifiko eta teknologikoarekin lotzen baitu aurrerapen ekonomiko eta politikoa. Zientziarekiko eta teknologiarekiko jarrera optimista horrek ekarri du, hain zuzen ere, gailentasun zientifiko eta teknologikoa herrialde askoren lehentasun nazional bilakatzea. 

Matematikak gizartean duen zentraltasun horrek eragina du matematika-hezkuntzan ere, eta matematikak ezagutza-arloen piramidean duen pribilegiozko posizio horren berri ematen duten hainbat elementu identifikatu ditut tesian; besteak beste, matematikari beste irakasgai batzuei baino garrantzi handiagoa aitortzen zaiola ikusi dut. 

Zergatik gertatzen da hori? Bada, matematikako kalifikazioak etorkizuneko arrakastaren adierazletzat hartzen direlako eta ikasleak hautatzeko eta etiketatzeko erabiltzen direlako. Izan ere, matematikari aitortzen zaion funtzioetako bat adimen-­neurtzailearena da. Horrez gain, matematika talentu akademikoaren bereganatzaile ere bada, hezkuntza-komunitatea saiatzen delako errendimendu akademiko altuko ikasleek matematikarekin lotutako ibilbide bat hauta dezaten. Errendimendu akademiko altua erakusten ez duten ikasleei, berriz, aditzera ematen zaie ez direla ikasketa horiek egiteko bezain onak. 

Ondorioz, matematikak segregazio-funtzio bat betetzen du. Halaber, matematikaren bereganatze- eta uxatze-taktikek erabaki akademikoak trebeziaren arabera hartzea sustatzen dute, eta guztiz bigarren mailan uztea gozamena. Gainera, matematikarako talentua esentzializatzen eta dikotomizatzen dute: matematikarako talentua ez da eskuratu daitekeen zerbait, baizik eta jaiotzatik badaukazun edo ez daukazun zeozer. 

Bigarren ibilbidea: erretratu desitxuratuak

Tesiak ez du talentu matematikoa modu dikotomiko eta esentzialista horretan ezaugarritzen. Aitzitik, eraikuntza ideologikotzat du, eta eraikuntza horrekin lotuta dauden elementu batzuk mahaigaineratzen ditu. Elementu horietako bat genero-­estereotipoak dira, gizonei eta emakumeei esleitutako ezaugarri eta jarrera desberdindu, historiko eta sozialki eraikiak, genero-identitate hegemonikoak naturalizatzen eta biologizatzen dituztenak, eta generoen arteko harreman baztertzaileak sustatzen. 

Matematika-hezkuntzarekin lotutako hainbat genero-­estereotipo daude. Esate baterako, pentsatu ohi da mutilak berez direla matematikarako hobeak, eta, bestalde, mutilen gaitasuna gehiegi balioesteko eta neskena gutxiesteko joera dago. Horrez gain, nesken arrakasta matematikoa esfortzuarekin eta obedientziarekin lotzen da; mutilena, aldiz, adimenarekin edota interesarekin. Porrota, nesken kasuan, matematika ulertzeko gaitasun ezari egozten zaio; mutilenean, berriz, irakaslearekin duten harreman kaskarrari edota laguntza faltari, adibidez.

Erretratu desitxuratu horiek eragindako hainbat fenomeno identifikatu ditut tesian. Matematika-­ikasleei dagokienez, matematikarako talentua performatzeak genero-egiazkotasuna eragin ohi du mutilen kasuan, eta genero-faltsutasuna neskenean. Izan ere, norbere burua matematikarako talentudun gisa aurkeztea bat dator maskulinitate hegemonikoarekin, baina feminitate hegemonikoarekin talka egiten du, genero-arauak haustea dakarrelako. Genero-estereotipoek matematika-­irakasleengan duten eraginari dagokionez, autoritate formala gizonei emakumeei baino errazago aitortzeak berekin dakar autoritate epistemikoa ere gizonei errazago aitortzea. Gizonezko irakasle bat ikasgelara sartzen denean, bere gorpuzkera dela-­eta, ikasleek emakume bati baino kasu gehiago egingo diote, eta, beraz, litekeena da irakasle horri matematikarako gaitasun handiagoa aitortzea, emakume matematika-irakasle bati baino.

Hirugarren ibilbidea: soinu-espazioaren jabetza

Matematika-hezkuntzan, genero-ikuspegitik, partaidetza ere elementu problematikoa da. Ikerketek diotenez, ikasle mutilek banakako laguntza gehiago jaso ohi dute, elkarrizketa gehiago hasten dituzte matematika-irakasleekin, eta talde handian sortzen diren elkarrizketetan ere jaun eta jabe izaten dira. Horrez gain, ikusgarritasun handiagoa dute, irakasleek mutilen izenak errazago ikasten eta gogoratzen dituztelako eta mutilen matematikarako talentua ere errazago identifikatzen dutelako. Talde-lanaren banaketa generizaturako joera ere badago: neskek sarriago egiten dituzte zeregin erreproduktibo eta ez-ikusgarriak, eta mutilek gehiagotan hartzen dute parte jarrera proaktiboa erakusteko bidea ematen duten jardueretan. 

Nesken partaidetza areagotzeko, irakasleak parte-­hartzearen kuotak kontrolatu behar ditu, ikasleek modu ahalik eta orekatuenean har dezaten soinu-­espazioa. Horretaz gainera, harremanak talde txikietan ardazteak talde handian parte hartzen ez duten ikasleen partaidetza-sentsazioa areagotzen lagundu dezake. Gainera, ezinbestekoa da irakasleak talde txikietan gertatzen ari den guztiari arreta jartzea eta dinamika baztertzaileetan esku hartzea. Azkenik, garrantzitsua da talde txikietan lan egitean elkar zaintzeko aintzat hartu beharreko arauak adostea, ikasle guztiak errespetatuak eta entzunak senti daitezen.

Laugarren ibilbidea: hutsegitea zigortzetik zaurgarritasuna aintzatestera

Matematikan, huts egiteak inpaktu handiagoa izan dezake neskengan mutilengan baino. Izan ere, neskek txikitatik ikasten dute, aintzat hartu eta balioetsi ditzaten, ondo heziak eta apalak izan behar dutela eta arauak errespetatu behar dituztela, perfekzioa eta edertasuna adieraztearekin batera. Mutilei, berriz, anabasa onartzen zaie, eta horrek inperfekzioan egoteko prestatzen ditu. Ondorioz, huts egiteak beldur handiagoa eragin ohi du neskengan mutilengan baino.

Hutsegitea zigortzeak beldur hori hauspotzen du, konfiantza matematikoa kaltetzen duelako. Lehiakortasunak ere inpaktu negatiboa du, eta, matematika-ikasleen kontaketetan, antsietate matematikoarekin lotuta agertzen da sarri. Hori genero-­ikuspegitik esanguratsua da, giroa lehiakorra denean antsietate matematikoa gehiago azaleratzen delako neskengan mutilengan baino.

Inertzia horiei aurre egiteko, porrotaren bestelako kudeaketa bat egin behar da. Hutsegitearekin lotutako esperientzia baikorrak eskaini behar zaizkie ikasleei, metakognizioa landuz edota hutsegitea jardun matematikoan integratuz, besteak beste. Izan ere, porrotari leku egiteak eta zaurgarritasuna erdigunean jartzeak hutsegitearekiko beldurrari, perfekzionismoaren alderdi kaltegarriei eta blokeoei aurre egiten lagundu dezake. 

Epilogoa: diziplinartekotasuna urrez nabarmentzen duen kartografia bat

Ikerketa hau matematikari batek egin du, baina ez matematikatik bakarrik: matematikaren didaktika eta ikasketa feministak ere funtsezko ezagutza-­iturriak izan dira. Horregatik, tesiaren azalean, goiko lau ibilbideak sinbolizatzen dituzten testurez gain, urre-koloreko trama bat ere badago, diziplinartekotasun hori ikusgai egin nahi duena (1. irudia). Urrezko tramak kintsugi teknika sinbolizatzen du, zeramikazko objektuak konpontzeko modu bat, zartadurak disimulatu beharrean urre-hautsarekin azpimarratzen dituena, arrakalak objektuen historiaren parte direlako eta, beraz, ezkutatu ordez, erakutsi eta balioetsi egin beharko liratekeelako. 

Batzuetan, kintsugi teknika hainbat lekutatik eratorritako zatiak elkartuz zerbait berria osatzean datza. Eta hori da, hain zuzen ere, tesi hau: nire ibilbide akademiko eta profesionala osatzen dituzten pusketak bateratzeko saiakera bat. Lanaren diziplinartekotasuna urrez nabarmentzen duen kartografia bat.

Bibliografia

[1] Black, L., Mendick, H., eta Solomon, Y. (editoreak). (2011). Mathematical relationships in education: Identities and participation. Routledge.

[2] Damarin, S. (2000). The mathematically able as a marked category. Gender and Education, 12(1), 69-85. https://doi.org/10.1080/09540250020418 

[3] Faulkner, W. (2011). Gender (in)authenticity, belonging and identity work in engineering. Brussels Economic Review, 54(2/3), 277-293. 

[4] Forgasz, H. J., Becker, J. R., Lee, K. H., eta Steinthorsdottir, O. B. (editoreak) (2010). International perspectives on gender and mathematics education. Age Publishing Inc.

[5] Fox Keller, E. (1985). Reflections on gender and science. Yale University Press.

[6] Fulmer, G. (2014). Undergraduates’ attitudes toward science and their epistemological beliefs: Positive effects to certainty and authority beliefs. Journal of Science Education and Technology, 23(1), 198-206. https://doi.org/10.1007/s10956-013-9463-7 

[7] Gates, P., eta Vistro-Yu, C. (2003). Is mathematics for all? In Second international handbook of mathematics education (31-73 orriak). Springer.

[8] Iriberry, N., eta Rey-Biel, P. (2019). Competitive pressure widens the gender gap in performance: Evidence from a two-stage competition in mathematics. The Economic Journal, 129(620), 1863-1893. https://doi.org/10.1111/ecoj.12617

[9] Kollosche, D. (2018). Social functions of mathematics education: A framework for socio-political studies. Educational Studies in Mathematics, 98(3), 287-303. https://doi.org/10.1007/s10649-018-9818-3 

[10] Ortega, L., Treviño, E., eta Gelber, D. (2021). The inclusion of girls in Chilean mathematics classrooms: Gender bias in teacher-student interaction networks. Journal for the Study of Education and Development, 44(3), 623-674. https://doi.org/10.1080/02103702.2020.1773064 

[11] Zouda, M. (2018). Issues of power and control in STEM education: A reading through the postmodern condition. Cultural Studies of Science Education, 13(4), 1109-1128.