Cartes

1995/10/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Sur la première carte on a utilisé la projection cylindrique centrale. La différence entre la première et la deuxième carte est évidente, même si la première est utilisée en plus d'une seconde.

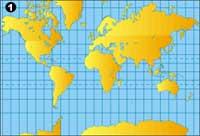
La raison de la première et de la deuxième réponse est liée à la première carte. Notre expérience visuelle nous donne une réponse et cela est basé sur la première carte, car c'est la première carte dans nos études et en dehors de la carte que nous avons vu le plus. La deuxième carte nous l'avons vu rarement et c'est pourquoi elle nous surprend. Cependant, les deux cartes sont correctes.

Où est la clé? Nous essaierons de l'expliquer. Les cartes sont des images plates de la terre ou des parcelles. Comment la terre (sphère) peut-elle être transformée en laun (plan) ? Quelles propriétés sont conservées dans cette conversion? Pour citer trois, gardez-vous des longueurs (distances), des angles et des surfaces ? En cela est la clé, la terre est ronde (sphère) et les cartes sont launas (plans)?

Cette conversion se fait par des projections cartographiques. La projection cartographique est le résultat de passer les points d'une surface sphérique (sphère) ou d'une partie de celle-ci à une surface laun (plan). Les particularités métriques de la sphère et du plan rendent impossible la conversion sans distorsion. Les cartographes inventent depuis longtemps et utilisent différentes procédures pour représenter la terre sur un plan. Cependant, si au passage de la sphère au plan, les distances sont maintenues, les angles et les surfaces sont déformés. Et si les surfaces sont exprimées avec précision, les formes, les angles et les distances sont opprimés. Donc, si vous voulez faire une carte, vous devez prioriser quelque chose.

Si la projection cache des longueurs (distances) est appelée équidistante, si les angles sont respectés, nous avons une bonne projection et si elle garde les surfaces est appelée projection équivalente. D'autre part, il existe des projections intermédiaires qui tendent à l'intersection entre deux ou trois propriétés, qui ne sont pas équidistantes, conformes ou équivalentes.

Sur la deuxième carte, la projection qui abrite les surfaces. La différence entre la première et la deuxième carte est évidente, même si la première est utilisée en plus d'une seconde.

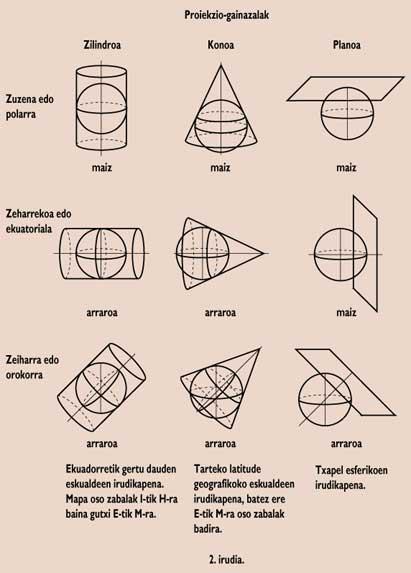
Mais comment se réalise la conversion, la projection ? Il y a plusieurs façons de le faire. Voyons en avant l'idée qui nous aidera plus tard (Figure 1). Si vous prenez un cylindre et que vous coupez et ouvrez ou élargissez de haut en bas par une droite, vous obtiendrez un morceau de plan. Inversement, en prenant une feuille, vous pouvez former un cylindre en forme de tube. Prenez maintenant un cône, coupez par une droite qui passe par le sommet et ouvrez-le, vous obtiendrez à nouveau un morceau de plan. Si vous essayez de faire la même chose avec la sphère, vous n'obtiendrez pas le même résultat. On dit que le cylindre et le cône sont des surfaces transparentes, mais la sphère n'est pas une surface transparente.

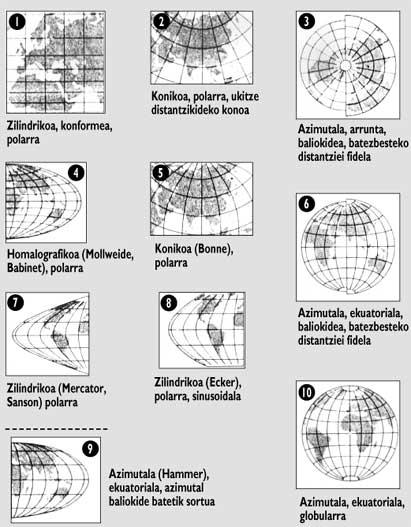
En tenant compte de cette idée, nous aurons trois possibilités de réaliser une carte : a) passer de la sphère au cylindre et du cylindre au plan, projection cylindrique ; b) passer de la sphère au cône et du cône au plan, projection conique ; c) passer de la sphère au plan, projection acimoutale.

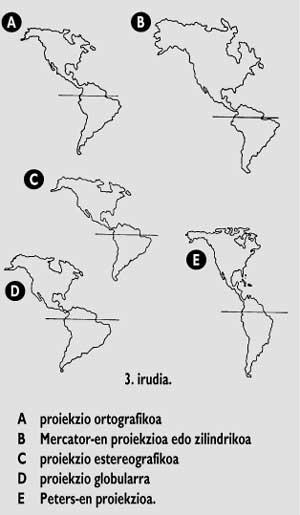
La projection peut être réalisée par des droites parallèles ou par des droites passant par un point. Dans la première, les droites peuvent être alignées avec le plan de projection (projection orthogonale) ou obliques (projection oblique). Dans le second, le point d'intersection des droites peut être le centre de la sphère (projection centrale ou gnomique); ou il peut être à la surface de la sphère (projection stéréographique); ou il peut être à l'infini (projection orthographique) (Figures 3 et 4).

La troisième carte est également correcte, même si elle n'est pas utilisée.

Sur la première carte a été utilisée la projection cylindrique centrale, la projection de Mercator. Cette projection augmente les surfaces proches des pôles, d'autre part, conserve les angles dans de petites régions, mais courbe les longs parcours (avions, bateaux, ...).

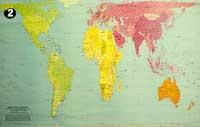
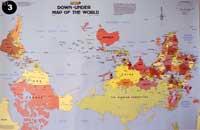
Sur la deuxième carte a été utilisé la projection qui abrite les surfaces, la projection de Peters. Distorsion des angles et des distances. Pour terminer, nous voulons poser une question sur l'utilisation et la projection cartographique. La différence entre la première et la deuxième carte est évidente, même si la première est utilisée en plus d'une seconde. Et en regardant la troisième carte, étant donné que la terre est dans l'espace, la troisième carte est également correcte, même si elle n'est pas utilisée.

Dans cette utilisation, des facteurs politiques et psychologiques prennent force. Nous qui vivons dans ces grands villages du Nord, il est bon que les pauvres y vivent, dans ces petits villages d'en bas. Que diriez-vous de notre pays dans le nord et plus grand que le reste? Ou, mélangeant la deuxième et la troisième carte, quelle influence aurait sur notre vie si nous pouvions voir notre peuple dans le sud et plus petit que le reste?

Remarque: L'Afrique a une superficie de 30.300.000 km ^2. La superficie de la Sibérie est de 12.765.000 km ^2.