Cuadrado mágico
En esta ocasión queremos analizar el tema de los cuadros de brujas. Como es sabido, para que sea un cuadrado de brujas tiene que cumplir las siguientes condiciones:
- estar formado por diferentes números.
- que la suma de los números en todas las columnas, filas y diagonales sea la misma.
Por ejemplo
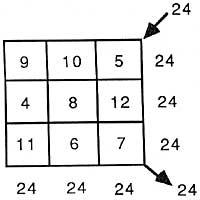
Parece que este tema de los cuadros de brujas es muy antiguo y parece ser una invención de la matemática china. A. C. Unos 1000 años antes eran conocidos este tipo de cuadrados en aquellos territorios de Extremo Oriente.
Pero han pasado los años, y como estamos en la era de la Informática, lo que tenemos de propostas en este número es preparar un programa que genere cuadros de brujas de diferentes niveles.

Así lo hemos hecho y os adjuntamos las siguientes líneas. No obstante, este programa sólo genera cuadrados impares (3,5,7,9,11...). La razón es muy sencilla: todos los cuadrados a nivel impar se forman siguiendo la misma regla, pero esta regla no es válida si el nivel cuadrado es par. A este tema, es decir, el tema de los cuadrados con nivel par, lo dejamos para un artículo posterior.
Antes de explicar el programa, nota final: como es posible que el número más pequeño de un cuadrado de brujas sea cualquiera, nosotros hemos elegido un valor aleatorio del rango 1-10. Por tanto, el programa creará de forma aleatoria 10 cuadrados diferentes por nivel.
El nivel más alto que puede generar este programa es 49, ya que las variables están dimensionadas hasta ese valor. Si queremos un nivel más alto deberíamos cambiar esta dimensión.
3º Curso: Cuadrado de bruja 3 x 3 suma de filas, columnas y diagonales = 24 |
5º curso: Cuadrado de bruja 5 x 5 suma de filas, columnas y diagonales = 70 |
7º curso: Cuadrado de bruja 7 x 7 |
9º curso: Cuadrado de bruja 9 x 9 suma de filas, columnas y diagonales = 441 |
Nivel 11: Cuadrado de bruja 11 x 11 suma de filas, columnas y diagonales = 726 |
MD1
La amenaza roja lanzada en el número anterior, que no dábamos respuestas, ha dado su primer fruto, y aunque os resulte difícil creer, debéis saber que hemos recibido la primera respuesta de los juegos propuestos. La noticia proviene de Arrasate. José Ramón Zubizarreta nos ha enviado una magnífica respuesta a un juego propuesto. Ahí tenéis la respuesta. Animaros a enviar más respuestas. "Estimado: Respuesta al juego matemático propuesto en la revista de diciembre: Podemos pensar que el número es de cifras A, B, C. Número de 6 cifras: ABCABC. Este número se puede escribir de la siguiente manera: A x 10 5 + B x 10 4 + C x 10 3 + A x 10 2 + B x 10 + C (m.m.) Reciba un cordial saludo y hasta otro." |
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian











