Magic Square
This time we want to analyze the topic of witch paintings. As is known, to make it a square of witches you have to meet the following conditions:
- be formed by different numbers.
- that the sum of the numbers in all columns, rows and diagonals is the same.
For example
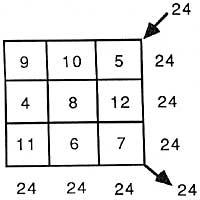
It seems that this topic of witch paintings is very old and seems to be an invention of Chinese mathematics. A. C. About 1000 years earlier this type of square was known in those Far Eastern territories.
But the years have passed, and as we are in the era of Informatics, what we have of propostas in this issue is to prepare a program that generates pictures of witches of different levels.

We have done so and we attach the following lines to you. However, this program only generates odd squares (3,5,7,9,11...). The reason is very simple: all squares at odd level are formed following the same rule, but this rule is not valid if the square level is even. To this topic, that is, the topic of squares with even level, we leave it for a later article.
Before explaining the program, final note: as it is possible that the smallest number of a witch square is any, we have chosen a random value of range 1-10. Therefore, the program will randomly create 10 different squares per level.
The highest level this program can generate is 49, since the variables are dimensioned to that value. If we want a higher level we should change this dimension.
3rd Course: Witch Square 3 x 3 sum of rows, columns and diagonals = 24 |
5th year: Witch square 5 x 5 sum of rows, columns and diagonals = 70 |
7th year: Witch Square 7 x 7 |
9th year: Witch Square 9 x 9 sum of rows, columns and diagonals = 441 |
Level 11: Witch Square 11 x 11 sum of rows, columns and diagonals = 726 |
MD1
The red threat launched in the previous issue, which we did not give answers, has borne its first fruit, and although it is difficult for you to believe, you must know that we have received the first response from the proposed games. The news comes from Arrasate. José Ramón Zubizarreta has sent us a magnificent response to a proposed game. There you have the answer. Encourage you to send more answers. "Dear: Answer to the mathematical game proposed in the December magazine: We can think that the number is of figures A, B, C. Number of 6 figures: ABCABC. This number can be written as follows: A x 10 5 + B x 10 4 + C x 10 3 + A x 10 2 + B x 10 + C (m.m.) Receive a cordial greeting and even another." |
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian











