A beleza do caos

1993/12/01 Barragués, J.I. | Alcalde, Cristina Iturria: Elhuyar aldizkaria

• Fisika

Dise que a ciencia clásica termina cando se crea o caos. Mentres os científicos trataban de ver unha orde (una regra representada por ecuacións matemáticas de valor universal) mentres estudaban as leis da Natureza, o mundo vivía de costas á aparencia desordenada da realidade.

As volutas dunha onda, os altibaixos da poboación, as desordes atmosféricas (tanto dos cantiis costeiros como das distintas formas que aparecen na neveira), a acumulación de estrelas nunha galaxia e o armazón de vasos sanguíneos son exemplos desta parte irregular da Natureza. Esta parte descontinua aparece como una controvertida ante os seres humanos.

Sistemas dinámicos

Durante séculos analizáronse os fenómenos da Natureza desde unha perspectiva analítica. O sistema analítico considera detalladamente cada parte dun fenómeno. Con todo, esta perspectiva ten erros paira aprender fenómenos moi difíciles. Outra solución é o enfoque sistemático. Segundo isto, o mellor é ter una visión xeral dos fenómenos, aínda que se perdan detalles.

O enfoque sistemático baséase na noción de sistema dinámico. O sistema dinámico é una colección de obxectos que están interrelacionados e evolucionan ao longo do tempo segundo un conxunto de normas.

Os sistemas dinámicos son abundantes na Natureza. Sistema ecolóxico (onde presas e predadores, fame, pragas, secas, ataques humanos, etc.). existen), é un exemplo de sistemas dinámicos. As relacións entre os veciños determinan si cada especie sobrevive ou se perde.

Os científicos que tentan aprender sistemas dinámicos elaboran copias simplificadas ou modelos (corrixidas mediante ecuacións matemáticas) e tratan de facer funcionar aproximadamente como un sistema real. Introducen o modelo no computador e ven como evoluciona ao longo do tempo e en que medida cambia cambiando os parámetros.

Por exemplo, o sistema ecolóxico pode incluír climas diferentes, número de habitantes, índice de natalidade, alimentos diarios necesarios, comportamento animal, etc. O modelo pode acabar coa perda dunha especie, cando hai demasiada comida pobre ou presa, ou cando hai equilibrio entre especies. Todo depende da introdución dos parámetros.

En ocasións, os analistas do sistema analizan o estado final dun sistema e tentan reconstruílo paira investigar as causas que levaron ao sistema a esta situación. Un exemplo soado foi o seguinte: na civilización maya VIII. Un modelo paira explicar o colapso ocorrido no século XX.

O moderno estudo do caos comezou na década dos 60 cun inconveniente descubrimento: un conxunto de ecuacións matemáticas de aparencia simple, capaz de describir sistemas dinámicos creados por condicións de comportamento ríxido e iniciais. As pequenas diferenzas na situación inicial xeran grandes diferenzas na evolución do sistema. A isto chamar efecto bolboreta. Esta palabra (no medio broma) indica que o movemento das ás dunha bolboreta, realizado aquí e agora, inflúe na climatoloxía de Pequín do mes seguinte.

Na década dos 70, un grupo de científicos traballou paira abrir camiño no reino da desorde. Eran matemáticos, físicos, biólogos, sociólogos, economistas e fisiólogos. Buscaban explicacións sobre a irregularidade que vían nos seus traballos, utilizando un novo sistema de análise.

Vinte anos despois, o termo caos converteuse nunha descrición detallada dunha tendencia (movemento científico). Aumento de conferencias, programas de investigación e publicacións. Botando sobre unha mesa saíron uns artigos sobre a estraña dinámica dunha pelota, xunto con outros sobre mecánica cuántica.

A ciencia da desorde creou unhas técnicas baseadas no uso de computadores. Estas técnicas ofrecen imaxes do caos, estruturas fascinantes, hipnóticas, delicadas e de dificultade infinita.

En realidade, os modelos matemáticos que tratan de mostrar un sistema ecolóxico, climatolóxico, económico ou outros sistemas de gran dificultade, están formados por miles de ecuacións e requiren moito tempo de procesamiento por computador.

Con todo, existen algúns modelos que se formulan con poucas relacións e que teñen una gran dificultade.

Un modelo matemático simple pode partirse dun valor inicial ao que _{denominaremos} de principio e, tras uns cálculos, crear un valor final: De acabado. Este último valor introdúcese no modelo como valor inicial e así sucesivamente. A reintroducción da saída como entrada se denomina realimentación. Hai realimentación, por exemplo, cando un micrófono toma a saída do amplificador. Ao final, o efecto
é insustentable.

Inicial ₌ 1,1

e calculemos o seu cadrado. Calcúlase novamente _o cadrado do valor do Xbucal obtido, etc. A secuencia de números obtidos será a seguinte: 1,21; 1,4641; 2,14358881;...

Seguide sacando as contas. Pero lentamente os números son cada vez máis
grandes, sen límites.

Inicial ₌ 0,99

coa seguinte secuencia: 0,9801; 0,96059601; 0,922744694; ... Lentamente, pero esta sucesión achégase a cero. Sorprende que os números tan próximos entre si (1,1 e 0,99) teñan un comportamento tan
diferente.

De acabado _{= (de} inicio)2

Utilizouse a norma. Tamén podemos utilizar outras fórmulas que se nos ocorran e ver o comportamento. Por exemplo:

De _{acabado =} R.Xinicio (1 _{- De} inicio)

relación, onde R é calquera número que se elixe ao principio. Esta fórmula chámase ecuación loxística e era una das primeiras que se estudaban.

En lugar de tentar interpretar a sucesión de números que se obtén, pódese reproducir gráficamente. No eixo horizontal situaremos os valores de R, por exemplo entre 2 e 5. No eixo vertical paira o punto inicial

(Inicial _{= 0,6,} p. ex.)

Situaremos a sucesión dos valores obtidos. A figura 1 mostra a representación gráfica do resultado. Aparecen ramas que se separan até o infinito.

Atractor de Lorenz

En 1963, Edwarz Lorenz estaba a analizar os remolinos que se producen por quecemento e arrefriado das capas atmosféricas. O fenómeno modelizado mediante un sistema de ecuacións, que parecía sinxelo, representou gráficamente o percorrido da partícula que se deixa dentro dun remolino.

A imaxe obtida, hoxe clásica, deu a coñecer a difícil estrutura oculta nas ecuacións e converteuse na bandeira dos primeiros examinadores do caos. Na figura 2 móstrase a atracción de Lorenz.

Como meteorólogo, Lorenz publicou o seu descubrimento na revista “Journal of the Atmospheric Sciences”, lonxe das mans de físicos, biólogos e enxeñeiros.

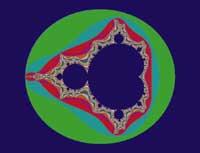
Fractales

Benoit Mandelbrot, matemático investigador que traballou na empresa IBM, inventou un novo elemento que máis tarde chamou fractal.

Mandelbrot viu una imaxe coñecida en diferentes lugares: á altura dos prezos das mercadorías, sorprendeu aos enxeñeiros en problemas de ruídos nas liñas telefónicas, etc. En todos eles víase a mesma característica, una firma que denunciaba o caos. Cando se analizaban máis detalladamente, as regras da evolución eran cada vez máis difíciles.

Os artistas atopan a beleza ideal en imaxes clásicas como liñas, planos e esferas, una estrutura armoniosa. Con todo, a realidade mostra una xeometría complexa, rota e mesturada. Descontinuidades, ruídos de súpeto e comportamentos estraños foron descritos por Mandelbrot mediante conceptos matemáticos abstractos. O fractal dános una vía paira modelar esta complexa realidade.

As curvas fractales poden xerarse por medio dun computador e teñen unhas formas fascinantes, como se mostra nas Figuras 3-10. Corais, galaxias e dragones fractales representan criaturas tan complexas como as que nos rodean.

A figura 11 mostra una imaxe do planeta Acua-Tor. É un planeta en forma de toroides cuxa superficie mariña está cuberta por un plasma fractal. Se o lector fíxase nel, verá pronto algunhas especies que loitan por sobrevivir en Acua-Torre.