Kaosa Eguzki-sisteman

1. irudia. Lorenz-en ur-gurpila edo noria.

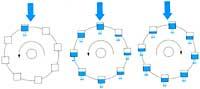
Azken hiru hamarkadetan zientzilariak ahalegin handiak egiten ari dira sistema dinamiko ez-linealen jokaeraren azalpenera hurbiltzeko. Uste ez bezala, sistema horiek ez dute beti oreka-egoeretara edo jokaera periodikoko egoeretara eboluzionatzen. Lehenengo aldiz E. Lorenz-ek 1963an frogatu zuenez, sistema dinamiko ez-linealak sarritan bilakaera erabat kaotikoa izaten dute. Aztertu zituen hiru ekuazio diferentzial ez-linealeko eta hiru ezezaguneko sistemak, Lorenz-en ur-gurpil edo noria deitzen den trensaren jokaera deskribatzen du. Adibide egokia da zein sistema-mota eta zein jokaerari buruz ari garen ulertzeko. Lehenengo irudian dugu eskema. Ura uniformeki erortzen da goiko iturritik. Ontziak zulatuta daude eta horiek ere uniformeki galtzen dute ura.

Iturriaren emaria txikia bada, goiko ontzia ez da beteko eta marruskadurak higitzea galeraziko du. Ur-emaria nahikoa handia bada, gurpila biratzen hasiko da. Tresnak biraketa-abiadura konstantea har dezake eta higidura horretan etengabe segi. Iturriaren jarioa handiagoa baldin bada, biraketa azkarragoa izango da eta sistemaren ez-linealtasunak garrantzi handiagoa hartuko du. Orduan, ontziek denbora gutxiago izango dute betetzeko, eta bestalde, oso gutxi hustuko dira igotzen hasi aurretik. Ondorioz, igotzen ari diren ontziak astunagoak gerta daitezke jaisten ari direnak baino eta biraketa alderanztu egingo da.

Lorenz-ek aurkitu zuenez, tresna bere kasa utziz gero biraketa norantzaz askotan alda daiteke, ez du inoiz abiadura konstanterik izatean eta ezta aurresan daitekeen sistema bihurtuko duen beste inolako jarraibiderik ere. Jokaera hau da Eguzki-sisteman aurkitu dena ere. Objektuaren orbitaren berezitasunak milaka edo milioika urtetan ziklikoki aldatuz eboluzionatu ondoren, bapatean beren jokabidea aldatu egiten dute. Alferrik da ordurarteko higidura ezagutzea, une horretatik aurrera bilakaera aurrikusi ezingo delako. Adibideak ematen hasi aurretik, beste ezaugarri bat ere aipatu behar dugu.

Eguzki-sisteman objetuaren orbitaren berezitasunak milaka edo milioika urtetan zikliko aldatuz eboluzionatu ondoren, bapatean beren jokabidea aldatu egiten dute.

Zientzilariek, lanean ari zireneko eremua edozein izanik ere, beti onartu izan dituzte hasierako baldintzetan egiten diren aldaketa txikiek (prozesuan zehar sor daitezkeen perturbazio txikiek bezala) emaitzetan aldaketa minimoak eragiten dituztela. Sistema kaotikoetan ordea, ez da horrelakorik gertatzen. Hain zuzen ere arazo horrek eraman zuen E. Lorenz sistema dinamiko ez-lineala aztertzera. Bere hasierako asmoa, iragarpen meteorologikak egiteko eguratsa egoki deskribatzea zen. Horretarako tenperatura, presioa eta haizearen abiadura aldagaiak lotzeko ekuazio egokiak idazten saiatu zen. Azkenik, hamabi ekuazioko sistema batekin hasi zen lanean. Sistema ez-lineala zen, noski. Beraz, analitikoki askaezina. Horregatik garai hartako ordenadore primitibo baten laguntzaz baliatu zen, zenbakizko metodoak erabiliz.

Hasierako datuak sartzean, garrantzirik gabekotzat kontsideratu zuen oso diferentzia txiki batek egun gutxitara erabat eguraldi ezberdina sorterazten zuela ohartu zen: hasierako baldintzekiko menpekotasun sentikorra deitzen zaio fenomeno honi. Sarritan tximeleta-efektu ere deitzen zaio. Eguraldia, bada, epe luzera ezin da erabat aurrikusi. Tximeleta baten hegalaldiak sortutako perturbazioa ere nahikoa izan liteke egun gutxira eskualde bateko eguraldia aldatzeko.

Agian Eguzki-sistemako osagaien higidura aztertzea eguratsaren eboluazioa aztertzea baino errazagoa dela pentsa daiteke. Badirudi eguratsaren konplexutasuna eta Eguzki-sistemarena ezin daitezkeela konparatu, nahiz eta asteroi-deak ere kontutan hartu. Dena den, Eguzki-sistema aztertzeak planteatzen dituen arazo teorikoak ere oso handiak dira. Mekanikan bi gorputzen problema deitzen dena erraz aska daitekeen arren, hiru gorputzez osatutako sistemaren higidura deskribitzen duen ekuazio-sistema ezin daiteke analitikoki askatu. H. Poincare-k frogatutako emaitza honek ezinezko bihurtzen du sistemaren epe luzerako ebolu-zioa aurriskustea. Zailtasun hau gainditzeko, astronomoek pertur-bazio-teoriak erabiliz kalkulatu ohi dituzte orbitak. Ekuazioei gai egokiak atxikitzen dizkiete gorputz guztien eragina kontutan hartzeko.

Berrogeitamargarreneko hamarkadaren erdialdera, Eguzki-sistemaren antzeko sistema dinamikoei buruzko teorema batekin aurrerapen teorikoa lortu zen. Eguzki-sistemari aplikatuta, bere egonkortasuna aurresaten du, planeten masak eta orbiten eszentrikotasuna eta inklinazioa denboran zehar txikiak badira.

Eguraldia ezin da epe luzera erabat aurrikusi. Tximeleta baten hegalaldiak sortutako perturbazioa ere nahikoa izan liteke egun gutxira eskualde bateko eguraldia aldatzeko.

Oinarri teoriko hauekin eta potentzia handiko lehenengo ordenadoreen ezinbesteko laguntzaz, Eguzki-sistemaren egonkortasunari buruzko lehen azterketa esanguratsua egiten hasi ziren. Adibidez, 1965ean kanpoaldeko bost planeten egonkortasuna hurrengo 120.000 urteetarako aurresan zen. Geroago epea milioi bat urtera luzatu zen, baina Plutonek Nepturorekin erresonantziak izaten dituela ere aurkitu zen. Orduan garrantzirik eman ez bazitzaien ere, elkarrekintza grabitatorio periodiko horiek gaur egun Eguzki-sistemaren kaosaren lehenengo arrastotzat kontsideratzen dira. 1985ean argitaratutako beste lan bateko azterketan, egonkortasun tartea 5 milioi urtera hedatu zen.

Aurrekoan bezala Plutonen erresonantziak azaldu ziren, baina artean aztertutako epea laburregia zen jokaera kaotikoa ager zedin. Hurrengo urtean J. Wydow eta G. Sussman-ek planeta berberen orbitei buruz lan egin zuten, lehenbizi aurreko 107 milioi urteetan eta etorkizuneko 110 milioi urteetan izan zuten eta izango duten itxura aztertuz, eta ondoren, bigarren epea 845 milioi urterarte luzatuz. Orbiten berezitasunak kalkulatzeko periodoa 32,7 egunekoa zen. Emaitza interesgarri batzuk, berehala aipatuko ditugunak ziren. Plutonen orbitaren inklinazioa 14,6° eta 16,9° bitartean aldatuko da (orain 17,2°koa da). Neptunok Plutoni eragiten dizkion erresonantzien ondorioz, azken planeta honek 3,8, 34, 150 eta 600 milioi urteko periodoko oszilazioak jasango ditu balera. Azkenik, Plutonen orbitaren hasierako baldintzak pixka bat aldatuz gero, orbita berria esponentzialki aldentzen da lehenbizi kalkulatutakotik. Batez ere azken bi emaitzak kaosaren adierazle dira.

Orainago LONGSTOP (Longterm Gravitational Stability Test for Outer Planets) izeneko azterketak ere Kaosaren adierazle izan daitezkeen fenomenoak azaltzen ditu ondorioetan. Adibidez, orbitek jasaten dituzten aldaketak txikiak direla egin bada ere, periodo irre-gularrekoak dira.

Barne-planetei buruzko azterketa bat ere bada; 1989an J. Laskar-ek aurkeztua. Zientzilari honek higiduraren ekuazioak analitikoki sinplifikatuta erabiliz barne-planeten orbitak kalkulatu ditu, 500 urteko urratsetan, hurrengo 200 milioi urterako. Kanpo-planetek bezala barnekoek ere aldaketa txikiak izaten dituzte orbitetan, baina hasierako baldintzekiko menpekotasun sentikorra nabaria da. Bestalde, erresonantziak ere azaltzen dira. Dena den, kaos-arrasto hauek ez digute planetak elkarren orbitak gurutzatu eta hondamendiak sorterazten ikusi behar ditugunik pentsarazi behar. Arazoa beste era honetara planteatzen da: planeten orbitak gehiegi aldatu ez arren ere, epe luzera ezingo dugu inolaz ere planetaren posizioa zein izango den aurresan.

Neptunok Plutoni eragiten dizkion erresonantzien ondorioz, azken planeta honek 3, 8, 34, 150 eta 600 milioi urteko periodoko oszilazioak jasango ditu batera. Azken bi emaitzak kaosaren adierazle dira.

Orain arte planeten orbitaren egonkortasunari buruz aritu gara, edo bestela esanda, kaosak orbita horietan duen eraginaren garrantziaz. Egitura osoari begira beste galdera batzuk ere plantea genitzake: zein izango da kaosaren eragina Eguzki-sistemaren itxuraketan?. Gaur egun duen itxura eta egonkortasun erlatiboa, eratu berri zela lehenengo milaka urteetan lortu al zituen, ala dituen ia 5.000 milioi urteetan zehar lortu ditu?

Batzuen ustez posible da garai batean beste planeta batzuk ere egotea, geroago jokaera kaotikoan erori eta kanporatu egingo zirelarik, baina, jakina, ezinezkoa da horrelakorik frogatzea. Beste batzuek, berriz, kaosaren eragina mugatua izan dela uste dute, asteroide eta beste gorputz txikien dinamikari bakarrik eraginik. Maila honetako kaos-kasu zehatzago eta nabariagoak hurrengo alean ikusiko ditugu.