Teorías de Kaluza e Klein: un mundo de once dimensións

1987/04/01 Martinez Lizarduikoa, Alfontso Iturria: Elhuyar aldizkaria

• Fisika

1.- Modelo e gravitación de Kaluza

A distancia, o cable parece una liña curva. Máis cerca, con todo, vemos que o punto P é un círculo. É posible que no espazo da tridimensión o que normalmente consideramos como punto sexa un pequeno círculo ao redor doutra dimensión espacial. Esta é a idea básica de Kaluza e Klein na teoría unificadora das forzas electromagnéticas e gravitatorias.

O antigo soño de Einstein (unir o campo gravitatorio e electromagnético coa descrición xeométrica) foi reinventado polo físico polaco Theordor Kaluza e cara a 1921 tratou de expresar por xeometría a teoría electromagnética de Maxwell. Pero paira levar a cabo este proxecto era necesario remodelar a propia xeometría para que a Electromagnética se moldiera dentro desa xeometría.

Paira logralo, Kaluza postulou una dimensión espacial adicional, co que a xeometría que depende da natureza tería catro dimensións espaciais e un tempo. A gravitación neste mundo de cinco dimensións sería o resultado da suma da gravidade normal e do campo electromagnético de Maxwell. Si fósemos capaces de ampliar a nosa percepción en cinco dimensións, atopariámonos/atopariámosnos cun único campo de forza: o gravitatorio. Segundo esta teoría, a onda electromagnética sería a ondulación da dimensión quinta.

A teoría de Kaluza obtivo un gran éxito matemático. Pero tamén tiña una cola insuperable. É dicir, si o universo espacial é de catro dimensións, por que non se pode captar fisicamente a cuarta dimensión? Esa cuarta dimensión será só una maña matemática?

2.- Estrutura pentadimensional de Klein

En 1926 o físico sueco Óscar Klein tratou de demostrar a compatibilidade da estrutura pentadimensional e mecánica cuántica de Kaluza. Paira iso, proporcionou una nova versión da ecuación de Schrödinger adaptada ás cinco dimensións. Paira Klein, a cuarta dimensión espacial ten una existencia real.

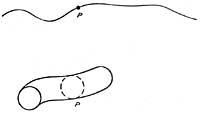
Paira entender mellor isto, supoñamos una liña e un círculo asociado a cada punto desa liña. A unión da liña dunha dimensión co círculo dunha dimensión crea un cilindro de dúas dimensións. Supoñamos tamén un plano no que todos os puntos dese plano están adaptados a un círculo, entón a unión entre o plano bidimensional e o círculo dunha dimensión creará un en tres dimensións continuas.

Co mesmo razoamento pódese adiviñar que en cada punto engádeselle un continuo tridimensional e un círculo, que están rizados na cuarta dimensión. Estes bucles non se rizarían no espazo, porque non están dentro do espazo. O que fan estes espirales é expandir o espazo.

Klein comezou o cálculo das circunferencias destes círculos que crean un universo de cinco dimensións. Paira iso tivo en conta as cargas de electróns e outras partículas, como as forzas gravitatorias entre elas. En caso de realizar os cálculos, indicou que a lonxitude destes círculos sería de entre 10 e 30 cm.

A súa pequena cifra indícanos por que a quinta dimensión non pode ser percibida correctamente. Esta cifra é tan pequena que, ademais dun ser vivo, ningún átomo podería moverse por estas dimensións.

Esta dimensión está situada dentro do átomo. Paira detectar una estrutura tan sutil, deberiamos dispor dun acelerador de fraccións de varios anos de luz.

3.- Generalización de modelos de Kaluza-Klein: un mundo de once dimensións

O modelo de Kaluza/Klein foi esquecido durante varios anos. Con todo, nos últimos anos xurdiu a paixón deste modelo entre os científicos, pero agora nun contexto diferente: É dicir, no contexto das Teorías de Maior Unión e as Teorías Supergravitatorias.

Co obxectivo de unir as forzas da natureza, nunha teoría propuxéronse sete dimensións descoñecidas do Universo. Pódese expresar como una estrutura compacta pequena, coma se cada punto da esfera tivese en cada momento una esfera adherida. As esferas situadas nas interseccións das liñas de coordenadas son dimensións adicionais agrupadas postuladas na nova teoría. As esferas son tangentes en cada punto respecto ao plano. Ademais, a esfera e o plano xeran só catro dimensións e non 11 da teoría. As catro dimensións son as catro coordenadas que definen un punto.

A teoría de Kaluza/Klein hase reintegrado no campo da Física, supondo que a simetría dos campos de forza é o resultado dunha estrutura xeométrica interna na Natureza. É máis, as simetrías gauge son formas de xeometría engadidas ás novas dimensións espaciais.

Os problemas que debería cubrir a teoría xeneralizada de Kaluza/Klein son o tres seguintes. Primeiro terá que encher un campo fermónico paira indicar os fermiones que hai no noso universo. Tamén debería indicar polo menos un campo bosónico e, por suposto, o campo gravitatorio (orixe das dimensións espirales ocultas). O modelo que cumpre todos estes requisitos é una versión da supergravedad 11. Por tanto, a moderna teoría de Kaluza/Klein postula un universo de 11 dimensións. Sete destas once dimensións estarían enroladas até un nivel no que quedarían ocultas paira a observación directa.

Ás dimensións nas que aparecen enrolados correspóndenlle un gran número de tipos de topologías, polo que hai que levar a cabo un proceso concreto paira elixir a máis adecuada:

Resolver ecuacións de supergravedad. Algunhas destas medidas poderían corresponder a catro dimensións espazo-temporais e a unha forma topológica pechada de sete dimensións. A continuación, estudariamos o conxunto de simetrías de cada superficie correspondente á resolución de ecuacións. O conxunto de simetrías defínenos a teoría non abelina gauge que debe unirse á gravidade. As diferentes superficies pechadas presentan distintos tipos de simetrías, e cada una delas define una Teoría diferente das Grandes Unións.
1. Finalmente, analízanse as estruturas de ondas estacionarias permitidas por superficies pechadas. Estas estruturas definirán as características das fraccións que predí a teoría nun espazo-tempo normal de catro dimensións.

4.- Heptaesfera

En todas as topologías que se poden conseguir, os matemáticos elixiron una topología especial polas súas características: Heptaesfera (equivalente en sete dimensións da esfera). Mediante este modelo descríbense todas as estruturas que van desde o átomo máis pequeno até a galaxia máis grande.

Se esta esfera de sete dimensións se deforma, pode aparecer o ocultamiento das simetrías e a ruptura brusca. Por estas razóns este modelo foi considerado óptimo.

Sería posible sondar e detectar fisicamente esta esfera?. Segundo cálculos recentes, a lonxitude da circunferencia desta heptaesfera é de entre 10 e 32 cm. Esta dimensión sitúase xunto á menor distancia con sentido físico utilizada en Física, a distancia de Planck.

A diferenza do principio de incerteza de Heisenberg paira sondar a heptaesfera de Kaluza/ /Klein sería 1019 veces maior que a masa do protón. Neste nivel enerxético podemos ver una estrutura espacial temporal de once dimensións. Pero paira conseguilo necesitariamos un acelerador de fraccións tan grande como a Vía Láctea de Ortz.

Con todo, nas investigacións levadas a cabo nos últimos anos xurdiron importantes problemas que en moitas ocasións non son conciliadores co mundo de catro dimensións que nós coñecemos e estudamos. Uno destes problemas é: En todos os mundos de once dimensións analizados predíse a existencia de neutrinos dextrógiro e levógiro. Isto non se corresponde coa experiencia que temos. No noso mundo todos os neutrinos son levógiros.

Una partícula pequena con forma de cordón ou corda ten una soa dimensión. Na teoría das supercuerdas, as cordas son extremadamente pequenas e móvense nun espazo e tempo similar de 10 dimensións. As propiedades da teoría das supercuerdas paira as páxinas do universo están a investigarse na actualidade e están estreitamente relacionadas con algúns problemas importantes da matemática contemporal.

Hai outro problema. As dimensións enroladas nos mundos de Kaluza/Klein dan una gran curvatura a outras dimensións espazo-temporais. Isto crea una gran contradición coas observacións astronómicas actuais, xa que segundo estas últimas a curvatura media do universo é practicamente nula.

5.- Perspectivas actuais

Os problemas mencionados e os infinitos da gravitación cuántica estiveron presentes nos últimos anos. Na actualidade (segundo os avances realizados ao longo de 1985) fálase dun universo de dez dimensións entre científicos e a chamada teoría das Supercuerdas (1) paira explicar este universo xerou grandes expectativas.

Chegados a este punto, lembraremos que o desenvolvemento das teorías gaudí non abelianas que se utilizan tardou uns dez anos en desenvolverse. Por iso, paira reforzar as relacións entre a supergravedad e as teorías de Kaluza/Klein, é posible que pasen varios anos. Mentres tanto, haberá que desenvolver traballos teóricos e matemáticas especiais que impliquen estas teorías.

O binomio Matemática/Física ten cada vez máis importancia. O descubrimento matemático que impulsou a teoría física da supergravedad foi o número máis anticonmutante. A matemática que necesita a teoría física da gravitación cuántica está aínda por crear.

OBSERVACIÓNS

Nesta nova teoría, as fraccións básicas (quantos) substitúense por unhas cordas en vibración. A cada vibración correspóndelle una fracción. Nesta superteoria combínanse a teoría das cordas e a supersimetría.