Teories de Kaluza i Klein: un món d'onze dimensions

1987/04/01 Martinez Lizarduikoa, Alfontso Iturria: Elhuyar aldizkaria

• Fisika

1.- Model i gravitació de Kaluza

A distància, el cable sembla una línia corba. Més a prop, no obstant això, veiem que el punt P és un cercle. És possible que en l'espai de la tridimensión el que normalment considerem com a punt sigui un petit cercle al voltant d'una altra dimensió espacial. Aquesta és la idea bàsica de Kaluza i Klein en la teoria unificadora de les forces electromagnètiques i gravitatòries.

L'antic somni d'Einstein (unir el camp gravitatori i electromagnètic amb la descripció geomètrica) va ser reinventat pel físic polonès Theordor Kaluza i cap a 1921 va tractar d'expressar per geometria la teoria electromagnètica de Maxwell. Però per a dur a terme aquest projecte era necessari remodelar la pròpia geometria perquè l'Electromagnètica es moldiera dins d'aquesta geometria.

Per a aconseguir-ho, Kaluza va postular una dimensió espacial addicional, amb el que la geometria que depèn de la naturalesa tindria quatre dimensions espacials i un temps. La gravitació en aquest món de cinc dimensions seria el resultat de la suma de la gravetat normal i del camp electromagnètic de Maxwell. Si fóssim capaços d'ampliar la nostra percepció en cinc dimensions, ens trobaríem amb un únic camp de força: el gravitatori. Segons aquesta teoria, l'ona electromagnètica seria l'ondulació de la dimensió cinquena.

La teoria de Kaluza va obtenir un gran èxit matemàtic. Però també tenia una cua insuperable. És a dir, si l'univers espacial és de quatre dimensions, per què no es pot captar físicament la quarta dimensió? Aquesta quarta dimensió serà només una aragonesa matemàtica?

2.- Estructura pentadimensional de Klein

En 1926 el físic suec Oscar Klein va tractar de demostrar la compatibilitat de l'estructura pentadimensional i mecànica quàntica de Kaluza. Per a això, va proporcionar una nova versió de l'equació de Schrödinger adaptada a les cinc dimensions. Per a Klein, la quarta dimensió espacial té una existència real.

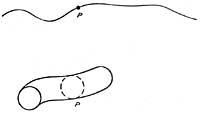
Per a entendre millor això, suposem una línia i un cercle associat a cada punt d'aquesta línia. La unió de la línia d'una dimensió amb el cercle d'una dimensió crea un cilindre de dues dimensions. Suposem també un pla en el qual tots els punts d'aquest pla estan adaptats a un cercle, llavors la unió entre el pla bidimensional i el cercle d'una dimensió crearà un en tres dimensions contínues.

Amb el mateix raonament es pot endevinar que en cada punt se li afegeix un continu tridimensional i un cercle, que estan arrissats en la quarta dimensió. Aquests bucles no s'arrissarien en l'espai, perquè no estan dins de l'espai. El que fan aquests espirals és expandir l'espai.

Klein va començar el càlcul de les circumferències d'aquests cercles que creguin un univers de cinc dimensions. Per a això va tenir en compte les càrregues d'electrons i altres partícules, com les forces gravitatòries entre elles. En cas de realitzar els càlculs, va indicar que la longitud d'aquests cercles seria d'entre 10 i 30 cm.

La seva petita xifra ens indica per què la cinquena dimensió no pot ser percebuda correctament. Aquesta xifra és tan petita que, a més d'un ésser viu, cap àtom podria moure's per aquestes dimensions.

Aquesta dimensió està situada dins de l'àtom. Per a detectar una estructura tan subtil, hauríem de disposar d'un accelerador de fraccions de diversos anys de llum.

3.- Generalització de models de Kaluza-Klein: un món d'onze dimensions

El model de Kaluza/Klein va ser oblidat durant diversos anys. No obstant això, en els últims anys ha sorgit la passió d'aquest model entre els científics, però ara en un context diferent: És a dir, en el context de les Teories de Major Unió i les Teories Supergravitatorias.

Amb l'objectiu d'unir les forces de la naturalesa, en una teoria s'han proposat set dimensions desconegudes de l'Univers. Es pot expressar com una estructura compacta petita, com si cada punt de l'esfera tingués a cada moment una esfera adherida. Les esferes situades en les interseccions de les línies de coordenades són dimensions addicionals agrupades postulades en la nova teoria. Les esferes són tangents en cada punt respecte al pla. A més, l'esfera i el pla generen només quatre dimensions i no 11 de la teoria. Les quatre dimensions són les quatre coordenades que defineixen un punt.

La teoria de Kaluza/Klein s'ha reintegrat en el camp de la Física, suposant que la simetria dels camps de força és el resultat d'una estructura geomètrica interna en la Naturalesa. És més, les simetries gauge són formes de geometria afegides a les noves dimensions espacials.

Els problemes que hauria de cobrir la teoria generalitzada de Kaluza/Klein són els tres següents. Primer haurà d'emplenar un camp fermónico per a indicar els fermions que hi ha en el nostre univers. També hauria d'indicar almenys un camp bosònic i, per descomptat, el camp gravitatori (origen de les dimensions espirals ocultes). El model que compleix tots aquests requisits és una versió de la supergravedad 11. Per tant, la moderna teoria de Kaluza/Klein postula un univers d'11 dimensions. Set d'aquestes onze dimensions estarien enrotllades fins a un nivell en el qual quedarien ocultes per a l'observació directa.

A les dimensions en les quals apareixen enrotllats li corresponen un gran nombre de tipus de topologies, per la qual cosa cal dur a terme un procés concret per a triar la més adequada:

Resoldre equacions de supergravedad. Algunes d'aquestes mesures podrien correspondre a quatre dimensions espaciotemporals i a una forma topològica tancada de set dimensions. A continuació, estudiaríem el conjunt de simetries de cada superfície corresponent a la resolució d'equacions. El conjunt de simetries ens defineix la teoria no abelina gauge que ha d'unir-se a la gravetat. Les diferents superfícies tancades presenten diferents tipus de simetries, i cadascuna d'elles defineix una Teoria diferent de les Grans Unions.
1. Finalment, s'analitzen les estructures d'ones estacionàries permeses per superfícies tancades. Aquestes estructures definiran les característiques de les fraccions que prediu la teoria en un espaitemps normal de quatre dimensions.

4.- Heptaesfera

En totes les topologies que es poden aconseguir, els matemàtics han triat una topologia especial per les seves característiques: Heptaesfera (equivalent en set dimensions de l'esfera). Mitjançant aquest model es descriuen totes les estructures que van des de l'àtom més petit fins a la galàxia més gran.

Si aquesta esfera de set dimensions es deforma, pot aparèixer l'ocultació de les simetries i la ruptura brusca. Per aquestes raons aquest model ha estat considerat òptim.

Seria possible sondejar i detectar físicament aquesta esfera?. Segons càlculs recents, la longitud de la circumferència d'aquesta heptaesfera és d'entre 10 i 32 cm. Aquesta dimensió se situa al costat de la menor distància amb sentit físic utilitzada en Física, la distància de Planck.

La diferència del principi d'incertesa d'Heisenberg per a sondejar l'heptaesfera de Kaluza/ /Klein seria 1019 vegades major que la massa del protó. En aquest nivell energètic podem veure una estructura espacial temporal d'onze dimensions. Però per a aconseguir-ho necessitaríem un accelerador de fraccions tan gran com la Via Làctia d'Ortz.

No obstant això, en les recerques dutes a terme en els últims anys han sorgit importants problemes que en moltes ocasions no són conciliadors amb el món de quatre dimensions que nosaltres coneixem i estudiem. Un d'aquests problemes és: En tots els mons d'onze dimensions analitzats es prediu l'existència de neutrins dextrógiro i levógiro. Això no es correspon amb l'experiència que tenim. En el nostre món tots els neutrins són levógiros.

Una partícula petita amb forma de cordó o corda té una sola dimensió. En la teoria de les supercuerdas, les cordes són extremadament petites i es mouen en un espai i temps similar de 10 dimensions. Les propietats de la teoria de les supercuerdas per a les pàgines de l'univers s'estan investigant en l'actualitat i estan estretament relacionades amb alguns problemes importants de la matemàtica contemporal.

Hi ha un altre problema. Les dimensions enrotllades en els mons de Kaluza/Klein donen una gran curvatura a altres dimensions espaciotemporals. Això crea una gran contradicció amb les observacions astronòmiques actuals, ja que segons aquestes últimes la curvatura mitjana de l'univers és pràcticament nul·la.

5.- Perspectives actuals

Els problemes esmentats i els infinits de la gravitació quàntica han estat presents en els últims anys. En l'actualitat (segons els avanços realitzats al llarg de 1985) es parla d'un univers de deu dimensions entre científics i l'anomenada teoria de les Supercuerdas (1) per a explicar aquest univers ha generat grans expectatives.

Arribats a aquest punt, recordarem que el desenvolupament de les teories gaudí no abelianes que s'utilitzen va trigar uns deu anys a desenvolupar-se. Per això, per a reforçar les relacions entre la supergravedad i les teories de Kaluza/Klein, és possible que passin diversos anys. Mentrestant, caldrà desenvolupar treballs teòrics i matemàtiques especials que impliquin aquestes teories.

El binomi Matemàtica/Física té cada vegada més importància. El descobriment matemàtic que va impulsar la teoria física de la supergravedad va ser el número més anticonmutante. La matemàtica que necessita la teoria física de la gravitació quàntica està encara per crear.

OBSERVACIONS

En aquesta nova teoria, les fraccions bàsiques (quantos) se substitueixen per unes cordes en vibració. A cada vibració li correspon una fracció. En aquesta superteoria es combinen la teoria de les cordes i la supersimetría.