Cuando la ficción se hace realidad
2014/05/01 Azkune Galparsoro, Gorka - Ikertzailea eta irakasleaEuskal Herriko Unibertsitateko Informatika Fakultatea Iturria: Elhuyar aldizkaria
400
Cuántica, siempre cuántica
La idea científica que más se acerca al tipo de teletransporte que hemos visto en series como Start Trek es la teletransporte cuántico, cuyo objetivo es transportar un sistema cuántico desde el punto A hasta el punto B, sin ningún tipo de soporte o canal físico. Pero para entender todo esto correctamente tenemos que explicar algunas de las bases de la física cuántica. ¡No te asustes! Porque lo haremos de una manera muy sencilla.
Cajas y bolitas
Cuando hablamos de sistemas cuánticos hablamos de conceptos como átomos, electrones, protones o fotones. Para facilitar las cosas, los sistemas cuánticos serán unas bolitas especiales guardadas en unas cajas especiales. Estas bolitas pueden tener dos colores: rojo | G> o azul | U>. La primera peculiaridad de estas bolitas es que, mientras permanecen en el interior de la caja, pueden estar en un estado de combinación de | G> y | U> colores:
a | G> + b | U>
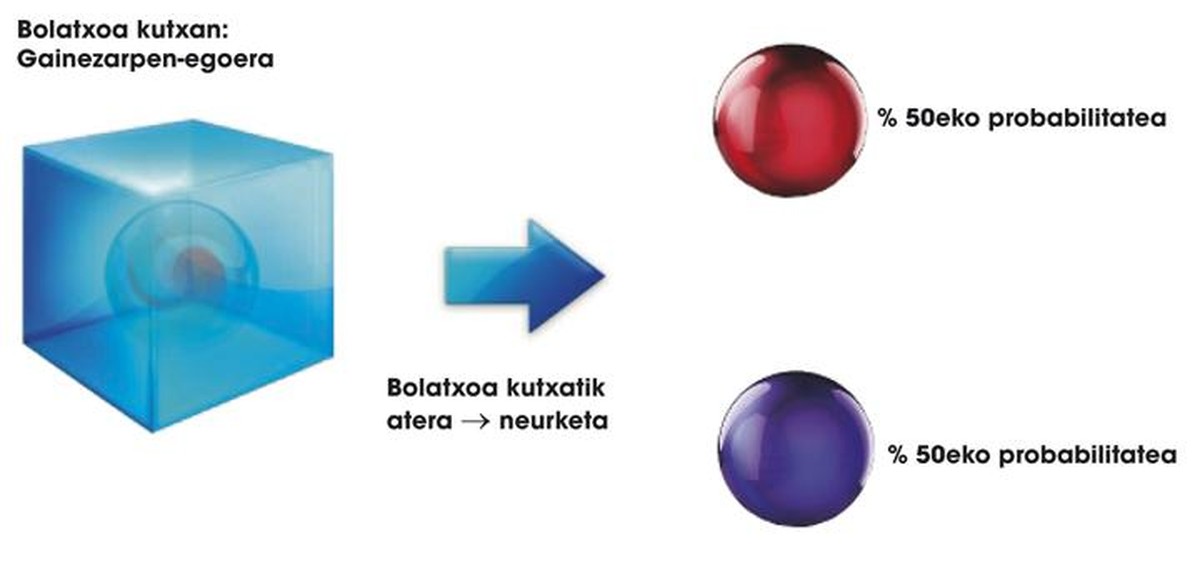
donde a y b son dos números reales. Su significado es sencillo: indican la probabilidad del color que tendrá la bolita al salir de la caja. Es decir, si una bolita se encuentra en estado 0,5 | G> + 0,5 | U>, al abrirse la caja la probabilidad de tener | G> es del 50%. En la cuántica esta propiedad de las bolitas se llama propiedad de la superposición. Esto nos lleva a otra ley especial: las bolitas dentro de la caja pueden estar en estado de superposición, pero cuando abrimos la caja sólo pueden ser | G> o | U>. No hay superposición fuera de caja. El sinónimo cuántico de apertura de caja es la medición, donde se anula el estado de solapamiento de las bolitas (ver figura 1).
Sin embargo, las cajas no se utilizan únicamente para guardar bolitas. Si agita la caja de forma diferente, podemos cambiar el estado de la bolita, por ejemplo cambiando las proporciones de las combinaciones. El equivalente al agitación son operaciones cuánticas. Hay muchos tipos y nosotros no vamos a profundizar. Por el momento, piensa que agitando la caja somos capaces de realizar las operaciones que deseamos.
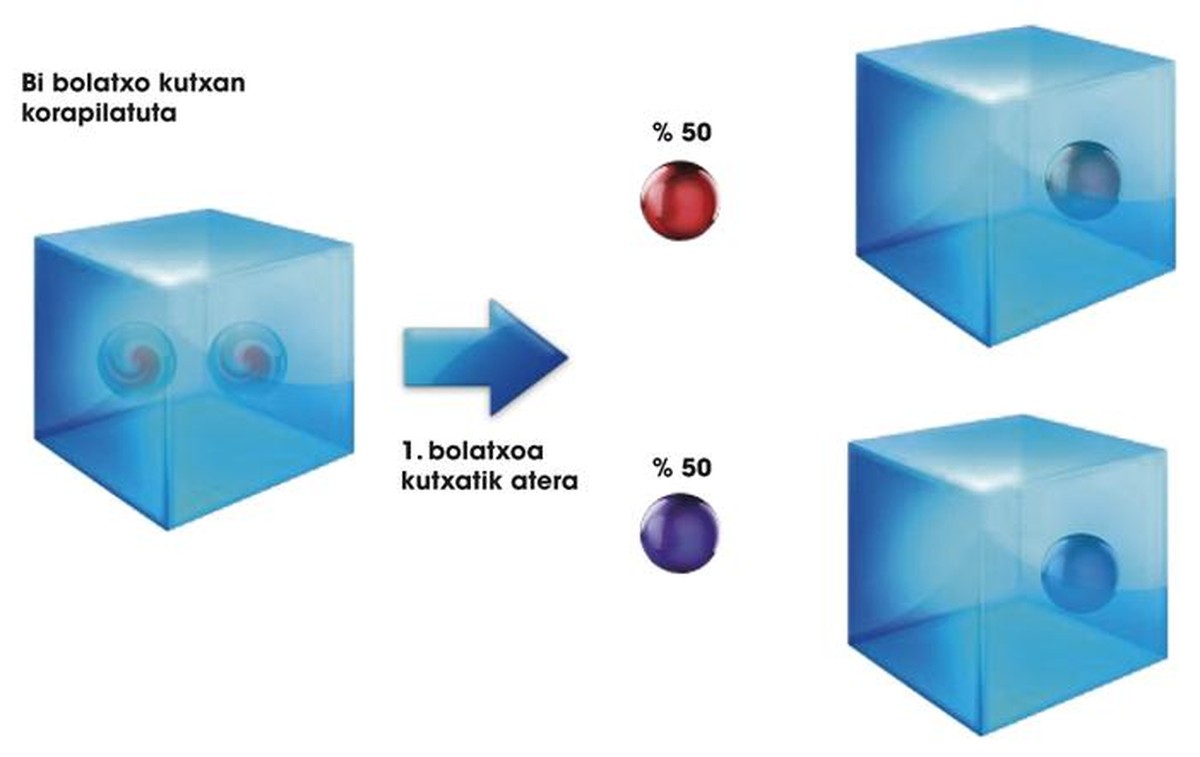
Para terminar con este apartado, tenemos que mencionar otra particularidad de nuestras cajas y bolitas. Si colocamos dos bolitas en la misma caja y agitamos la caja, podemos coronar las bolitas juntas. Así, agitando la Bolita 1 y la Bolita 2 en la misma caja, podemos obtener el estado 0,5 | G 1 G 2 > + 0,5 | U 1 U 2 >. En Cuántica, esta situación se llama complicada, ya que las dos bolitas quedan complicadas. En esta situación, si de la caja solo salimos la bolita 1 y vemos que está en estado | G>, ya sabemos que sin tener que salir de la caja, la bolita 2 estará en estado | G> (ver figura 2). Ten en cuenta que esto no es posible si las dos bolitas están en dos cajas, aunque estén superpuestas. En este caso, si sale la primera bolita y | G>, la segunda bolita puede ser | G> o | U>. No existe ninguna relación entre ambos.
Son muchos los estudios que se están llevando a cabo sobre las dificultades. Tras complicar dos bolitas se mantienen complicadas hasta que se realiza una medición, aunque la distancia entre ellas sea muy grande. Sea cual sea la distancia, la medida en una bolita actúa bruscamente sobre la otra bolita y cambia su estado aunque no la hayamos tocado. Todavía no sabemos por qué y cómo se complica, pero ya somos capaces de utilizarlo. Como se puede imaginar, es la clave para conseguir la teletransporte.
Telreporte cuántico
Tenemos dos buenos amigos, Alaitz y Beñat, y un día juntos decidieron complicar dos bolitas. Tras el enredo, cada uno cogió su bolita en una caja especial, sin mirar nunca a la bolita. Así, cuando cada uno se trasladaba a su casa, las dos bolitas seguían enredadas, a pesar de estar alejadas.
Alaitz tiene otra bolita en su casa, metida en otra caja, en un estado de superposición desconocido. Alaitz, amante de los retos, piensa: "¿Cómo puedo enviar a Beñat la nueva bolita en la situación en la que se encuentra sin moverte de casa? ". No puede sacar la bolita de la caja, ya que en este caso cambiaría su estado natural a | G> o | U>. Él quiere enviar la bolita a Beñat en su estado natural, esto es, a | G> + b | U> en situación de superposición. Alaitzena parece un reto difícil, ¿no?
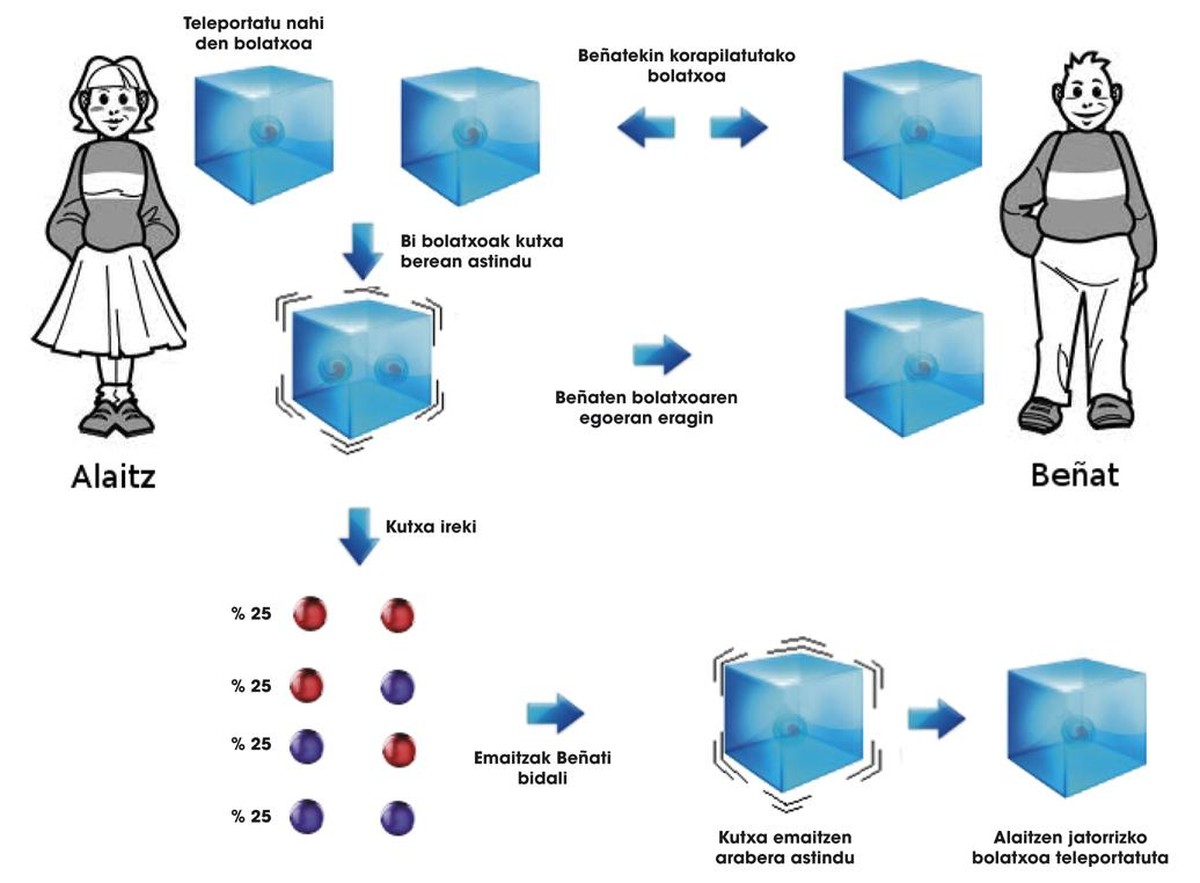
Pero como Alaitz es una chica inteligente, encuentra una solución. La bolita que quiere enviar a Beñat la coloca en la misma caja con la que ya tenía enredada con Beñat. Recuerda que Beñat tiene su bolita guardada en su casa. Alaitz realiza varias operaciones en las dos bolitas que tiene en sus manos, sacudiendo la caja de una manera especial. Como consecuencia del enredamiento, estas operaciones también afectan a la bolita de Beñat, y Alaitz sabe además su influencia. Por ello, abre la caja para conocer el estado de sus dos bolitas. Las bolitas pueden estar en estado | GG>, | GU>, | UG> o | UU> respectivamente. Según el resultado, Alaitz conoce el estado de la bolita de Beñat. Sorprendentemente, tras las operaciones de Alaitz, estas posibles situaciones son a | G> + b | U>, a | U> + b | G>, a | G> - b | U> y a | U> - b | G>.
Así que Alaitz, tan pronto ve sus dos bolitas, le llama Beñat y le dice cómo agita la caja de su bolita para conseguir la bolita que Alaitz quiere enviar. Cuántica nos ha demostrado que, sabiendo cómo azotar la caja, de las cuatro situaciones que hemos presentado, se puede obtener el estado original de la bolita de Alaitz. El proceso descrito se puede ver en la figura 3. Al final del proceso, la bolita de inicio de Alaitz ha sido telaudida en casa de Beñat!
¿Es la teletransporte cuántica la teletransporte de nuestros sueños?
La respuesta breve a esta pregunta es negativa. Según la física actual, no se puede conseguir algo parecido a la teletransporte de Star Trek. ¿Por qué? ¿Qué diferencias hay entre la teletransporte cuántica que acabamos de ver y la de Star Trek?
1. Entre Alaitz y Beñat nunca se han movido bolitas: El estado de la bolita inicial de Alaitz se ha copiado a la bolita de Beñat, pero no ha habido transporte de materia.
2. La teletransporte cuántico no es instantáneo. Para que se produzca el teletransporte, Alaitz debe informar a Beñat de la situación de sus dos bolitas por teléfono, correo electrónico o gritando. Esta comunicación puede producirse a la velocidad máxima de la luz pero no a la velocidad. Por lo tanto, la telreporte cuántico necesita un tiempo para llevarse a cabo y no puede superar la velocidad de la luz.
A pesar de los problemas, parece que, al menos teóricamente, podemos conseguir que una persona pueda teletransportarse. Pero ten en cuenta las dificultades técnicas:
1. Para llevar una bolita de teletrabajo tenemos que tener otra en la llegada (bolita de Beñat). Por lo tanto, tenemos que tener otras partículas en la meta de la persona que queremos teletransportar.
2. Las operaciones y medidas deberían realizarse teniendo en cuenta todas las propiedades de las partículas de una persona. En el caso de las bolitas, sólo hemos mencionado el color, pero las partículas cuánticas tienen muchas propiedades.
3. Deberíamos enviar toda la información de estos millones de medidas en destino utilizando los canales de comunicación habituales.
Eso es sólo el principio. En Cuántica ya se ha visto que es muy difícil mantener el nudo entre dos partículas, que deben ser aisladas del mundo. Por lo tanto, aunque no se desprecie del todo, podemos considerar casi imposible que una persona pueda teletransportarse. Además, y pasando a un ámbito más filosófico, ¿es la misma persona la que hemos teletransportado así? En definitiva, hemos copiado la información de una persona a otras partículas de materia. Dejamos la pregunta en el aire.
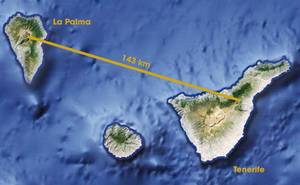
Sin embargo, con la tecnología actual ya se ha conseguido teletransportar fotones y algunos átomos. En el caso de los fotones, se consiguió la teladrinalización entre las islas de Tenerife y La Palma, imponiendo un récord de 143 km (ver figura 4). Las explicaciones de este experimento fueron publicadas en la prestigiosa revista Nature en 2012. Por su parte, investigadores de la Universidad de Maryland consiguieron en 2009 teletransportar un átomo a una corta distancia.
Teletransporte hoy y mañana
Dominamos la teletransporte cuántico a nivel teórico: se conocen las propiedades de la misma, sabemos cómo hacerlo y sabemos sus limitaciones. Tecnológicamente también se han dado pasos muy importantes, tal y como hemos explicado. Estamos convencidos de que en el futuro seremos capaces de teletransportar distancias más largas y mayores cantidades de información, pero ¿dónde está el límite? Quién sabe.
La telreporte cuántico será una tecnología muy importante en el futuro. Imprescindible en la criptografía cuántica, será una de las claves en el futuro para la obtención de ordenadores cuánticos. Seguramente se utilizará en aplicaciones que ahora no podemos imaginar, que en principio sólo existía en el ámbito de la ficción.
En Euskal Herria tenemos el honor de ser un grupo de investigadores punteros en estos temas. El grupo Quantum Technologies for Information Science1, del Dr. Enrique Solano, que vino de la mano de Ikerbasque a Leioa, ya goza de gran prestigio internacional. Ejemplo de ello es el artículo publicado en la revista Nature en 2010.
Aquí y allá, los investigadores nos aportarán un nuevo conocimiento sobre nuestro fascinante mundo. La telreporte cuántico nos abre nuevas puertas, pero nadie puede saber qué va a estar detrás de ellas. Como dice Pedro Miguel Etxenike, el nuevo conocimiento aumenta el desconocimiento, ya que cada respuesta plantea mil nuevas preguntas.
Bibliografía
Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia
