Baixo a influencia da relatividad xeral

1991/10/01 Martin Axpe, Iñaki Iturria: Elhuyar aldizkaria

• Fisika

Cando Einstein publicou en 1905 a Teoría da Relatividad Especial (TUE), o concepto que tiñamos sobre o tempo volveu ser relativo. Dez anos despois, con todo, sorprendeunos aínda máis: o espazo e o tempo que coñecemos... son curvos. Pero de que falaba cando lle curvó?

Elhuyar. Ciencia e Técnica

fronte

No número de, vimos EBT. Entón dixemos que EBT só serve cando o observador se move a velocidade constante. Observadores con aceleración

a)

en TC necesitamos una teoría máis xeral, a Teoría da Relatividad Xeneral (TCE). Esta teoría, ademais de ser máis rara que a TUE, require una formulación matemática máis difícil. Por iso, a regra e o reloxo

a)

veterano

A pesar da sinxeleza de atopar demostracións da UET, as explicacións sobre EOT son moito máis reducidas. En calquera caso, trataremos de achegarse con atención ao colectivo de lectura paira non escorrentar ao lector

...

EBT e gravitación

A gravitación, una lei que explica a atracción mutua dos planetas (e de todos os corpos con masa), foi ideada por Newton (ver figura 1-A), que serviu paira explicar o que se vía na práctica ao longo dos séculos… salvo algunhas excepcións. Pero como xa se comentou, a TUE esixe una modificación das fórmulas, polo que a TUE obriga a que a fórmula tradicional adopte a forma indicada na figura 1-B. Con todo, os resultados da nova fórmula non coinciden coa experiencia. Pola contra, son aínda peores que os da fórmula antiga.

Por iso, chegamos a unha situación na que, por unha banda, EBT non serve paira os observadores en aceleración e, por outro, non é capaz de explicar a gravitación. En base a isto, pensar que pode existir certa relación entre aceleración e gravitación parece bastante lóxico, e o traballo de Einstein foi demostrar esa relación.

Espazo/tempo e TSE

Todos os eventos realízanse nun lugar e tempo. Sen espazo e sen tempo non hai nada, non ocorreu nada que non ocorra en ningún sitio nin en ningún momento con claridade. O espazo/tempo é, por tanto, a base, estrutura ou envase do mundo.

Hai tempo que todo o corpo que Galileo cedera (tanto pesado como lixeiro) caía coa mesma aceleración era coñecido, pero non lle deu importancia.

Agora pensemos que una bicicleta que percorre a rúa salta nun lugar concreto. Pensaremos que a causa pode ser a bicicleta, o ciclista, a estrada ou o vento. Pero máis tarde un coche salta no mesmo lugar, e o mesmo pásalle a un autobús e a un camión. Una vez visto isto, diremos que a razón do salto non ten que ver cos vehículos, senón coa natureza da base, é dicir, coa estrada. O mesmo dixo Einstein, é dicir, que a caída de todos os corpos coa mesma aceleración débese ao envase, ao ser espazo/tempo (ver figura 2).

Doutra banda, e dado que o espazo/tempo é ou é imprescindible para que ocorra algo, o espazo/tempo afecta a todos os corpos. Por tanto, na natureza non hai fracción libre, e como un observador ou un corpo debe ser libre paira circular a velocidade constante, non hai observadores inerciales (v=cte.) tamén. En consecuencia, non hai observadores privilexiados. Todos os observadores son equivalentes, é dicir, alcanzamos una relatividad total, xa que xa non temos que facer ningunha restrición (TEE v=cte. solicitábanos).

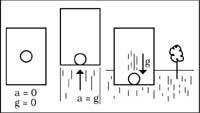
Por exemplo, un astronauta grita no espazo e cae contra unha parede. Non será posible que o home saiba se esta caída débese á inercia da aceleración do buque ou á gravitación dun planeta

Pero como se formula esta forma de ser espazo/tempo? E como se relaciona cos movementos dos corpos?

Características espazo-temporais

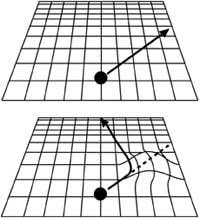
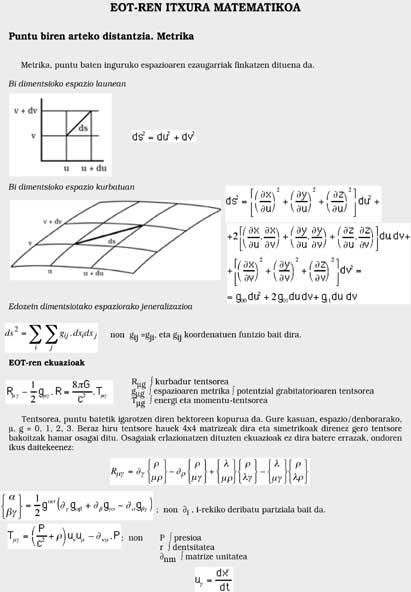
Antes habemos visto que a caída dos corpos débese á forma espacial/temporal. Se este espazo/tempo é chairo non afectará. En caso de ser curvado, pola contra, afectará (ver figura 4). Por iso, é o noso espazo/tempo curvo. Lamentablemente ten catro dimensións (tres paira o espazo e outra paira o tempo), polo que non podemos ver esa curvatura. Pola contra, os matemáticos non coñecen fronteiras e expresan a métrica espazo-temporal con total facilidade. Os que dominan as matemáticas poden mirar ao cadro, pero os demais mellor non mirar.

Vexamos agora a segunda característica. Nas teorías antigas (incluída a TUE, e noutras teorías gravitatorias actuais), o espazo/tempo era ríxido, é dicir , era un recipiente de sucesos, pero sen influír nos feitos. Pola súa banda, EOT reivindica que o espazo/tempo tamén é un obxecto dinámico, é dicir, que os obxectos e sucesos deforman o espazo//tempo e viceversa, as deformacións espazo-temporais afectan o comportamento de obxectos e sucesos (ver figura 5).

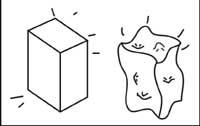
Por tanto, ademais de ser un espazo/tempo curvo, tamén é dinámico.

O último paso de Einstein foi identificar estas deformacións coa gravitación. Explicou máis ou menos que até agora una masa atraía sen medios nin recursos a obxectos da súa contorna. Segundo Eot, pola súa banda, una masa deforma espazo-tempo e esta deformación condiciona as traxectorias dos obxectos da súa contorna (ver figura 6).

Deu á teoría un reflexo matemático a través de varias fórmulas. Estas fórmulas relacionan a natureza do espazo/tempo, a curvatura e as masas e enerxías en xogo, pero son tan complicadas que só as menciono no cadro.

Conclusións

Este características espazo-temporais xeran una serie de consecuencias. Os máis coñecidos son:

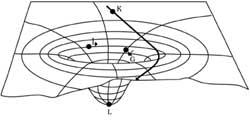
1. A traxectoria da luz se curva cando pasa polo lateral dunha masa, xa que a luz tamén é atraída pola gravitación (como se pode observar nas Figuras 6 e 7).
2. Canto máis grande é a gravación, máis lento van os reloxos.
3. Hai que crear ondas gravitatorias como as que aparecen na auga. ( Necesitámoslle porque aínda non se atoparon).
4. A consecuencia máis coñecida é o buraco máis negro. Así que imos analizalos máis amodo.

Buracos negros

Cando se resolveron por primeira vez as ecuacións de Einstein,

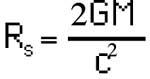
Constátase a ausencia de resolución de valores. Que pasaba a esa distancia? Nun principio pensouse que o corpo non podía ser menor desta medida, pero logo demostrouse que una estrela podía contraerse até un tamaño menor que ese valor. Entón entendeuse _que demontres era R s, un límite. Calquera cousa (incluso a propia luz) que se atope a unha distancia menor de R _s dun corpo non poderá escapar e caerase contra o corpo. Pero como a luz tampouco é capaz de escapar, nós non poderemos ver ese corpo. Por iso chámase buraco negro.

Exposición a ETAP

Que pasaría si o noso Sol (R _s) fose capaz de alcanzar esta medida? (En principio a masa é insuficiente paira conseguilo). Nun principio veríase contraído, cada vez máis pequeno. Posteriormente, a medida que se vaia reducindo, a súa cor faríase cada vez máis vermello e finalmente desaparecería. Por tanto, os planetas virarían ao redor do insignificante. De nada? Non, nós non veriamos o Sol, pero a súa masa estaría envolvida nun punto. A medida que nos achegamos a este punto non o veriamos, pero se nos achegamos a 3 km (porque R _s = 3 km paira o Sol) non poderiamos volver atrás. Una vez superados os 3 km, nós tamén (como a luz) quedariamos cativos e tirariamos contra o punto.

Paira detectar a densidade necesaria paira crear buracos negros, lembra o seguinte dato: O R _s da Terra é de 1 cm, é dicir, se toda a Terra estivese contraída até unha esfera de menos de 1 cm de radio, non poderiamos saír dela nin nos verían desde fóra. Ou noutras palabras, a nosa Terra debería contraela até 1 cm paira converterse nun buraco negro.

Coidado, con todo, coas viaxes: o noso corpo non tería nada que ver ou percibir porque sobreviviría o suficiente.

Tolo no mundo

Esta curvatura provocada polas masas débese a que o valor G é extremadamente baixo (G = ^6,672 x 10 -11). Pero que pasaría si ese valor fose moito maior? Paira empezar, non poderiamos vivir na Terra. A súa forza de atracción sería tan grande que nos pisaría contra o pavimento. As estrelas tampouco iluminarían o ceo como salpicón, xa que a maioría delas serían buracos negros. Todos os corpos que veriamos serían avermellados. E é que este mundo de G pequeno veríase como cando iluminas una habitación con lámpadas vermellas.

Tamén neste caso, por diferentes motivos, produciríase o paradoxo dos xemelgos. Se o día de Biki, dous nados, levásemos un deles á costa e o outro a unha cima, volvendo xuntarnos co paso do tempo, comprobariamos que o primeiro sería novo e o segundo ancián.

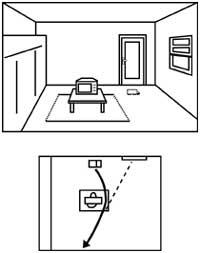
Ademais, teriamos una enorme dificultade paira determinar a localización dos obxectos en función da nosa posición (ver figura 7).

E de todo isto, ao final que?

Estes posibles exemplos poden estar moi ben, pero no día a día non percibimos en absoluto as curiosidades de EBT e EOT, nin o tempo relativo nin o espazo/tempo curvo. E a verdade é que aínda que a teoría ten moitas aplicacións científicas, non hai grandes erros en crer que o mundo que vemos é como o que sabemos.

Si, pero nós tampouco podemos romper a curiosidade, non podemos satisfacer a fame da causa. Calquera paso que nos axude a pór en evidencia as leis ocultas que ten o funcionamento do mundo resultará apaixonante. E é que as fantasías do esoterismo quedan pálidas ante a ET. Una vez máis, a realidade superou a ficción.

(Nota: Paira ver ben estas dúas últimas imaxes podes ir ao pdf).