Bajo relatividad especial

1991/09/01 Martin Axpe, Iñaki Iturria: Elhuyar aldizkaria

• Fisika

Elhuyar. Ciencia y Técnica

En dos artículos anteriores al , abordamos escalas de tiempo y medidas mundiales comparándolas con lo cotidiano. En esta ocasión abordaremos la Teoría de la Relatividad Especial.

Aún así, a pesar de que transcurrieron 86 años desde que se conoció por primera vez esta teoría, a menudo se le considera algo oculto, incomprensible y sasimágico. Todos sabemos quién fue Einstein: el sabio que puso la ciencia patas arriba, el científico solitario y genial que sabía mucho más que nadie, y muchos más tópicos. Así mitificamos Einstein, situándonos sobre un pedestal, lo convertimos en inaccesible y dejamos su teoría para algunos expertos. Pero podemos hacer algo más que conocerlo. En definitiva, si creemos que los habitantes del polo sur no se mueven de memoria, ¿por qué no creer lo que nos dice la Relatividad Especial?

En una simple articulación no abrimos los ojos ante la nueva verdad, claro, porque para ello hay que aprender con mucho esfuerzo, pero podemos acercarnos a las conclusiones.

Por tanto, no vamos a mostrar ninguna demostración. Asumiendo lo que dice la teoría y las consecuencias que de ella se derivan, cambiaremos de escala para que su esencia influya en nuestra vida cotidiana.

Teoría de la relatividad especial

La Teoría de la Relatividad de Einstein consta de dos apartados: el primero es la Teoría de la Relatividad Especial (que se representará con la abreviatura TUE), en la que se analizan los objetos de velocidad constante y el segundo, la Teoría de la Relatividad General (TGV), que se tratará en un artículo posterior.

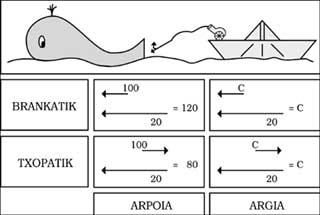
Pensemos que estamos en la atalaya de un pueblo de nuestra costa, explorando el mar abierto, y que vemos un barco que navega a 20 km/h. En un momento dado, el ballenero proyecta el arpón de proa a 100 km/h. Nosotros, por tanto, veremos salir el arpón a 120 km/h. Por el contrario, si en igualdad de condiciones el arpón es lanzado desde la chopa, lo veremos desde nuestra atalaya a una velocidad de 80 km/h. Dado que los movimientos del barco y arpón son de sentido contrario, sus velocidades tienden a eliminarse entre sí.

Hasta aquí no hay ningún obstáculo, pero ahora vamos a poner un foco de luz en el lugar del cañón arpón. Como la velocidad de la luz es de 300.000 km/s (se indica con el símbolo c), según el mismo razonamiento superior, nosotros deberíamos ver los rayos de luz desde nuestra atalaya a una velocidad de c+ 20 y c-20. Lo que pasa no es eso. De hecho, veremos los rayos que provienen tanto de la proa como de la chopa a la misma velocidad ( c). Es más, independientemente del movimiento del foco de luz, la velocidad de la luz se mantendrá indefinidamente (ver figura 1).

La experiencia nos enseña este curioso comportamiento que se opone a la lógica. Y que la máxima velocidad posible es la de la luz, es decir, que la velocidad c no se puede superar. Por lo tanto, el concepto (suma o resta de velocidades) aplicable en condiciones concretas no es aplicable en condiciones diferentes. ¿Eso significa que a veces las fórmulas (leyes) aplicables no pueden aplicarse en otras ocasiones? Einstein respondió que no y formuló la TUE de la siguiente manera:

1. En todas las condiciones son aplicables las mismas leyes.
2. La velocidad de la luz siempre es constante (en vacío) y nunca se puede superar.

Para completar el postulado anterior hay que huir de las viejas fórmulas de siempre y utilizar las nuevas que inventó Lorentz (ver figura 2).

Sin embargo, estas nuevas fórmulas traen consigo una serie de consecuencias más habituales.

Conclusiones

Sin darnos cuenta, al comprender y explicar el mundo que vemos, pensamos que hay velocidades infinitas. Por ejemplo, lo he visto cuando ha sucedido, pero para ello la velocidad de la vista debería ser infinita, o bien tardará un tiempo en recorrer el espacio desde el lugar donde ha ocurrido hasta mis ojos. Sin embargo, sabemos que la velocidad máxima es c, por lo que no hay velocidades infinitas. De aquí podemos sacar la primera conclusión: hay quien opina que los sucesos que ocurren simultáneamente no son simultáneos.

Por ejemplo, en el centro del barco hay un pescador y como los rayos que van por la proa y la chopa tienen que recorrer la misma distancia, los verá al mismo tiempo. Pero desde nuestra atalaya veremos que para que el rayo brancótico llegue hasta la mitad del barco tiene que recorrer un camino más corto que el chopático (ver figura 3). Por lo tanto, el brancánico llega antes y ¡no los vemos a la vez!

Siguiendo un razonamiento similar, veremos los objetos que se mueven con respecto a nosotros más cortos que cuando están parados, y cuanto mayor sea la velocidad, más corto será el objeto.

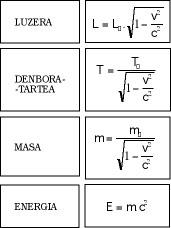
La tercera conclusión se refiere al tiempo y es bastante popular. Según esto, en los cuerpos en movimiento el tiempo pasa más despacio. Aunque parezca que no hay justificación para ello, es una consecuencia directa de las nuevas fórmulas. Por último, cabe mencionar que la masa en reposo de los cuerpos es más ligera que cuando se mueven y que la energía y la masa son lo mismo. El aspecto matemático de todo ello se refleja en la figura 4.

A pesar de que estas extrañas consecuencias pueden ser motivadas por la teoría, alguien podía pensar que en la vida cotidiana nunca se ha visto ese efecto. La verdad es que se han visto. Porque los ven todos los días... los que miran las fracciones básicas. La razón de ello radica en la velocidad: estos efectos sólo se producen cuando se encuentra cerca de la máxima velocidad en juego (empezando por los electrones y otras fracciones), y como las velocidades que sufrimos y vemos en nuestra vida están tan lejos del máximo, no percibimos nada especial.

No te desesperes. Para que la TUE sea un poco más cercana, más doméstica y más comprensible, os propongo un juego: cambiaremos la velocidad c.

Un día en carreras

Pensemos que la velocidad de la luz es de c = 30 km/h. Con esta condición los efectos del TUE serían evidentes en nuestra vida. Para empezar, nunca podríamos superar los 30 km/h independientemente del recurso. ¿Y qué otras diferencias observaríamos entonces?

Supongamos que es domingo y hemos ido a carreras de coches. Nos hemos sentado en la grada para ver la carrera desde allí, pero aún faltan unos minutos, por lo que analizaremos las características de cada detalle. Vemos que la pista es una recta de 2 km de longitud. Asimismo, en la salida hay tres coches preparados de 3 m de longitud (ver figura 5). Finalmente se ha iniciado la carrera con los coches A y D bastante igualados (29 y 29,9 km/h respectivamente), pero el B se ha lanzado por avería o lo que es imposible (5 km/h).

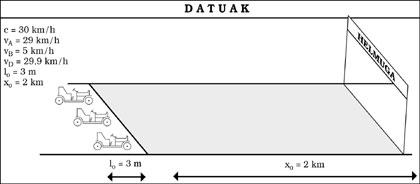
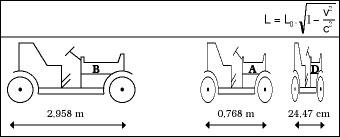
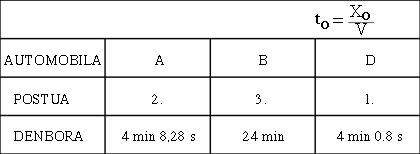
Al pasar por delante de nosotros, estos coches de 3 m de longitud parados veremos más cortos y, en concreto, cuanto más rápido vayamos, más cortos nos parecerán (ver figura 6). Sin embargo, una vez terminada la carrera, comprobamos que las tres de ellas tienen una longitud de 3 m. Mientras tanto, el ganador será D, por supuesto, los tiempos oficiales en meta serán los de la figura 7.

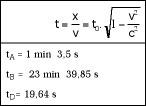
Si preguntamos a los pilotos, recibiríamos una imagen bastante diferente. Y es que aunque el criterio del conductor B coincidiera más o menos con el nuestro, las opiniones de A y D serían diferentes. Para A, por ejemplo, la pista sería de 512 m y defendería que D tenía 163 m (ver figura 8).

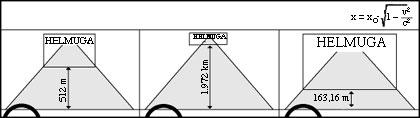
Lo mismo pasaría con los tiempos. Creemos que mientras la distancia entre A y D es de 7,5 segundos, consideran que ha sido mayor. Y es que nosotros hemos tardado 4 minutos en ir de la salida D a la llegada, pero ella sólo ha tardado 19 segundos en hacer lo mismo (ver figura 9). Por lo tanto, es más joven que si se hubiera detenido en la grada por la velocidad. ¡Eso es ahorrar tiempo!

La paradoja de los gemelos

Pero aquí surge una preocupación. Cuanto más ligero vaya el coche, más corto lo hemos visto y, simétricamente, los pilotos han visto los objetos de la pista cuanto más rápido es ir. En eso consiste precisamente la relatividad, es decir, uno piensa que el otro es más corto, pero el otro cree que el primero es más corto, y ni uno ni el otro tiene razón, o ambos tienen, porque las cosas no tienen el único aspecto real, sino que dependiendo del movimiento del observador van a adoptar distintas formas.

Y ahora viene la inquietud que he mencionado: nosotros hemos visto a los pilotos un poco más jóvenes, pero ellos a nosotros más antiguos y no más jóvenes como lo haría la simetría de la relatividad. ¿En el caso del tiempo no se cumple la relatividad? Este nudo se conoce como la paradoja de los gemelos. La respuesta es favorable al TUE. Veamos por qué.

Inicialmente se comentó que es aplicable en aquellos casos en los que no existe aceleración TEE (velocidad constante). Si la pista está parada, podemos considerar que los coches se mueven o que los coches se mueven cuando están parados, y tanto uno como el otro están rectos. Así que nosotros veremos que el tiempo va más despacio en los coches, y los pilotos verán que el tiempo va más despacio en la pista mientras la velocidad de los automóviles permanece constante. Aquí se cumple la simetría de la relatividad. Sin embargo, los automóviles deben sufrir una aceleración en el momento de su movimiento y un frenado final para detenerse.

En estos dos momentos especiales la simetría se rompe y no podemos decir que lo que se mueve (pista o coche) sea lo mismo. Dado que uno de ellos (el coche) tiene un movimiento especial, el piloto sabe que no está parado. La consecuencia es que los pilotos y los de pista estén de acuerdo para responder a la pregunta de dónde está el tiempo más lento.

Loco en el mundo

¿Y qué más pasaría en un mundo tan bajo?

A las 8’30 de la mañana Jone y Mikel han salido de casa porque tienen un examen en el Instituto de Bilbao. Ambos dejan una asignatura para aprender en el camino. Jone vive en Deusto. Por lo tanto, ha salido a pie y ha llegado en aproximadamente media hora, habiendo terminado la asignatura. Mikel, por su parte, al residir en Barakaldo, ha cogido a las 8,30 el Tren de Alta Velocidad (29,9 km/h) y ha llegado a las 9, pero no ha tenido tiempo de leer el comienzo de la asignatura, ya que apenas han pasado unos segundos en su vida interna.

Y por las mismas razones, los astronautas tendrían una vida muy dura. Supongamos que los espacios pueden circular a una velocidad de 29,999 km/h. En este caso, el viaje de ida y vuelta a la Luna pasaría tres años en la Tierra, mientras pasarían dos semanas en la vida del astronauta (incluida la estancia en la superficie de la Luna). Tras quince viajes a lo largo de su vida, el astronauta comprobaría que su mujer y sus hijos fueran sus mayores.

Y de todo esto, ¿al final qué?

Dicho esto, el TUE no tendrá ninguna incidencia ni en los trenes ni en nuestro modo de vida normal. Además, los efectos descritos no deben tomarse literalmente, sino como una aproximación. De hecho, los días y los años serían muy diferentes si hubiera c = 30 km/h. Lo que ves no es un auténtico resumen de cosas, sino una especie de giro y deformación. Cuanto mayor sea la velocidad de un objeto, más rojizo aparecería, etc. Pero todos estos detalles nos siguen igual (los curiosos pueden acudir al cuadro de Crítica de la idea resumen).

La idea que tenemos que retener es que en la naturaleza hay una velocidad máxima, la de la luz, lo que produce unos efectos extraños o anormales cuando nos acercamos a esa velocidad. Y por mi parte quisiera añadir la siguiente idea: Aunque las huellas del TUE son increíbles, son perfectamente comprensibles. Lo realmente sorprendente es que la teoría de Einstein sólo depende de unos pocos científicos. ¡Arraigo! No somos capaces de diseñar el motor de automóvil, pero entendemos las bases de funcionamiento. ¡Así sea también con el TUE!

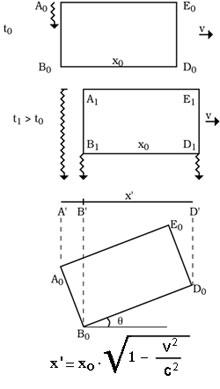
CRÍTICA IDEA RESUMEN Por este motivo no podemos ver el resumen. Supongamos un cuerpo A 0 B 0 D 0 E 0 que se mueve con velocidad v. Nosotros estamos alineados con la dirección del movimiento, estando la B 0 D 0 más cerca. Como sabemos, lo que sabemos en un momento determinado son los rayos que llegan simultáneamente en ese momento. Así, como se puede apreciar en la figura, los rayos que parten de A 0 a B 1 y D 1 llegarán a nuestros ojos simultáneamente. Lo que vamos a ver, por lo tanto, tal y como hemos explicado en el artículo, no es sólo un resumen B’D’, sino también una imagen oculta de A 0 B 0 lado A’B’. Pero esa forma de ‘A’B’D’ que vemos y el cuerpo con el ángulo q serían iguales a la imagen girada, como se ve en la imagen. Por lo tanto, cuando v está cerca de c vemos que las cosas giran y, al mismo tiempo, lo que hay detrás de las cosas es espectacular.