Elhuyar. Zientzia eta Teknika
ren aurreko artikulu bitan munduko denbora- eta neurri-eskalak jorratu genituen eguneroko gauzekin erkatuz. Oraingo honetan Erlatibitate Bereziaren Teoriari helduko diogu.
Oraindik ere, teoria hau lehenengoz ezaguterazi zenetik 86 urte igaro arren, zerbait ezkutu, ulertezin eta sasimagikotzat jotzen da maiz. Denok omen dakigu Einstein nor izan zen: zientzia hankaz gora jarri zuen jakintsua, inork baino askoz gehiago zekien zientzilari bakarti eta jeniala, eta hamaika topiko gehiago ere bai. Horrela Einstein mitifikatu, idulki baten gainean kokatuta eskuragaitz bihurtu eta bere teoria zenbait aditurentzat utzi dugu. Baina haren berri izatea baino zerbait gehiago egin dezakegu. Azken finean, hego poloko biztanleak buruz behera ez dabiltzala sinesten badugu, Erlatibitate Bereziak dioskuna zergatik ez sinetsi?
Artikuluxka xume batean ez ditugu begiak ziplo irekiko egia berriaren aurrean, noski; horretarako latz ikasi behar bait da, baina hurbil gaitezke ondorioetara.
Ez dugu, beraz, frogapenik azalduko. Teoriak esaten duena eta hortik ateratzen diren ondorioak onartuz, eskalaz aldatuko dugu, bere mamiak gure eguneroko bizitzan eragina izan dezan.
Erlatibitate bereziaren teoria
Einsteinen Erlatibitate-Teoriak atal bi ditu: lehena Erlatibitate Bereziaren Teoria (EBT laburduraz adieraziko duguna) da, zeinetan abiadura konstantea duten objektuak aztertzen diren eta bigarrena, Erlatibitate Orokorraren Teoria (EOT), zeina hurrengo artikulu batean jorratuko bait dugu.
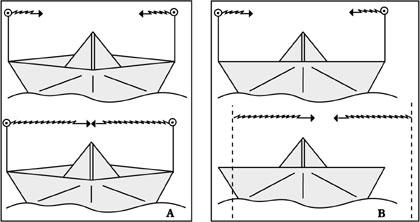
Pentsa dezagun gure kostaldeko herri bateko talaian gaudela itsaso zabala arakatuz, eta 20 km/h-ko abiaduraz nabigatzen duen balenuntzi bat ikusten dugula. Halako batean, balenuntziak brankako arpoia jaurtikitzen du 100 km/h-ko abiaduraz. Guk, beraz, 120 km/h-ko abiaduraz ikusiko dugu arpoia irteten. Alderantziz, baldintza berdinetan arpoia txopatik jaurtikitzen bada, 80 km/h-ko abiaduraz ikusiko dugu gure talaiatik; untzi eta arpoiaren higidurak kontrako norantzakoak direnez beraien abiadurek elkar ezabatzeko joera bait dute.
Honaino ez dago inolako oztoporik, baina orain arpoi-kanoiaren lekuan jar dezagun argi-foku bat. Argiaren abiadura 300.000 km/s-koa denez gero (c ikurraz adierazten da), goiko arrazonamendu berberaren arabera guk c+ 20 eta c-20 abiaduraz ikusi beharko genituzke argi-izpiak gure talaiatik. Gertatzen dena ez da hori baina. Izan ere brankatik zein txopatik datozen izpiak abiadura berberaz ( c abiaduraz) ikusiko ditugu. Are gehiago, argi-fokuaren higidura edozein izanik ere argiaren abiadurak berdin iraungo du (ikus 1. irudia).
Logikari aurka egiten dion portaera bitxi hau esperientziak irakatsi digu. Baita abiadura posiblerik handiena argiarena dela, hots, c abiadura ezin gaindi daitekeela ere. Beraz, baldintza konkretuetan aplikagarria zen kontzeptua (abiadura-batuketa edo -kenketa) ez da aplikagarri baldintza ezberdinetan. Batzuetan aplika daitezkeen formulak (legeak) bestetan ezin aplika daitezkeela esan nahi al du horrek? Ezetz erantzun zuen Einsteinek eta EBT honela formulatu zuen:
- Baldintza ezberdin guztietan lege berberak dira aplikagarri.
- Argiaren abiadura konstantea da beti (hutsean) eta inoiz ezin daiteke gainditu.
Lehengo postulatua betetzeko betiko formula zaharrak alde batera utzi eta Lorentzek asmatu zituen formula berriak erabili behar dira (ikus 2. irudia).
Baina formula berri hauek ohizkanpoko zenbait ondorio dakartzagute.

Ondorioak
Konturatu gabe, ikusten dugun mundua ulertu eta azaltzerakoan abiadura infinituak badaudela pentsatzen dugu. Adibidez, hori gertatu denean ikusi dut esan ohi dugu, baina horretarako ikusmenaren abiadurak infinitu izan beharko luke; edo bestela, gertatu den lekutik nire begietaraino espazio-tartea zeharkatzeko denbora-tarte bat behar izango du. Haatik, badakigu abiadura maximoa c dela eta beraz ez dagoela abiadura infiniturik. Hemendik lehengo ondorioa atera dezakegu: batzuen ustez aldiberean gertatzen diren gertakariak besteen ustez ez dira aldiberekoak.
Adibidez, balenuntziaren erdi-erdian arrantzale bat dago eta branka eta txopatik doazkion izpiek distantzia berdina zeharkatu behar dutenez gero, aldiberean ikusiko ditu. Baina gure talaiatik brankatiko izpiak untziaren erdiraino heltzeko txopatikoa baino bide laburragoa ibili behar duela ikusiko dugu (ikus 3. irudia). Beraz brankatikoa lehenago heltzen da eta ez ditugu aldiberean heltzen ikusiko!
Antzeko arrazonamenduari jarraituz, gurekiko higitzen diren objektuak geldirik daudenean baino laburragoak ikusiko ditugu, eta abiadura zenbat eta handiagoa izan, hainbat eta laburrago objektua.
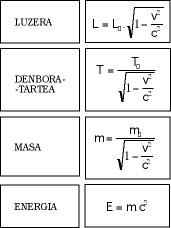
Hirugarren ondorioa denborari dagokio eta nahikoa ospetsua da. Honen arabera, higitzen ari diren gorputzetan astiroago igarotzen da denbora. Horretarako justifikaziorik ez dagoela iruditu arren, formula berrien ondorio zuzen-zuzena da. Azkenik, aipa dezagun gorputzen geldiuneko masa higitzen ari direnean baino arinagoa dela eta energia eta masa gauza bera direla. Guzti honen itxura matematikoa 4. irudian isladatzen da.
Ondorio bitxi hauek teoriak eskatutakoak izan badaitezke ere, eguneroko bizimoduan inoiz ez dela horrelako efekturik ikusi pentsa zezakeen norbaitek. Egia, ordea, ikusi egin direla da. Izan ere, egunero ikusten dituzte... oinarrizko zatikiei begiratzen dietenek. Horren arrazoia abiaduran datza: jokoan dagoen abiadura maximotik hurbil dagoenean soilik (elektroi eta beste zatikietan abididez) agertzen dira efektuok, eta gure bizitzan pairatu eta ikusten ditugun abiadurak maximotik hain urrun daudenez gero, ez dugu ezer berezirik somatzen.
Ez etsi baina. EBT zertxobait hurbilago, etxekoago eta ulergarriago izan dadin, joko bat proposatzen dizuet: c abiadura aldatu egingo dugu.
Egun bat lasterketetan
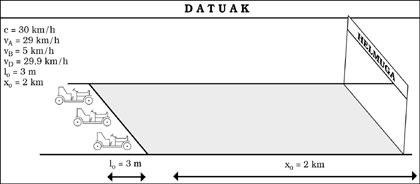
Pentsa dezagun argiaren abiadura c = 30 km/h-koa dela. Baldintza honekin EBTren efektuak nabariak lirateke gure bizimoduan. Hasteko, inoiz ezingo genuke 30 km/h-ko abiadura gainditu, baliabidea edozein izanda ere. Eta zein beste desberdintasun nabarituko genuke orduan?
Demagun igandea dela eta automobil-lasterketetara joan garela. Harmailatan eseri gara lasterketa handik ikusteko asmoz, baina oraindik minutu batzuk falta direnez, xehetasun guztien ezaugarriak aztertuko ditugu. Pista 2 km-ko luzera duen lerro zuzena dela ikusten dugu. Halaber, irteeran hiru automobil prestaturik daude; hirurak 3 m luzekoak (ikus 5. irudia). Azkenean, lasterketa hasi da, A eta D automobilak nahikoa parekaturik irten direlarik (29 eta 29,9 km/h-ko abiaduraz hurrenez hurren), baina B automobila, matxuraren bategatik edo, ezin astiroago abiatu da (5 km/h).
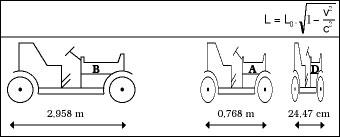
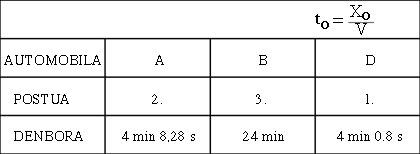
Gure aurretik pasatzean, geldirik zeudenean 3 m-ko luzera zuten automobil hauek laburragoak ikusiko ditugu, eta, konkretuki, zenbat eta azkarrago joan hainbat eta laburrago irudituko zaizkigu (ikus 6. irudia). Hala ere, lasterketa amaitutakoan berriz geldirik ikusi orduko hirurek 3 m-ko luzera dutela egiaztatuko dugu. Bitartean irabazlea D izango da, noski, helmugan aditzera emango dituzten denbora ofizialak 7. irudikoak izango direlarik.
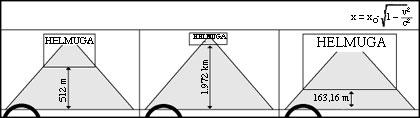
Pilotuei galdetzen badiegu, nahikoa irudi desberdina jasoko genuke. Izan ere B gidariaren eritzia gutxi gorabehera gurearekin bat baletor ere, A eta D-ren eritziak bestelakoak lirateke. A-ren aburuz adibidez, pista 512 m-koa litzateke eta D-k 163 m zituela defendatuko luke (ikus 8. irudia).
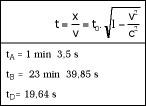
Gauza bera gertatuko litzateke denborei dagokienez. Gure ustez A eta D-ren arteko tartea 7,5 segundokoa den bitartean, beraien ustez handiagoa izan da. Izan ere, guk 4 minutu behar izan ditugu D irteeratik helmugaraino joaten ikusteko, baina hark 19 segundo soilik behar izan ditu gauza bera egiteko (ikus 9. irudia). Beraz harmailatan geldirik geratu balitz baino gazteagoa da abiaduraz joateagatik. Hori da denbora aurreztea, hori!
Bikien paradoxa
Baina kezkatxo bat sortzen da hemen. Automobilak zenbat eta arinago joan, hainbat eta laburragoak ikusi ditugu eta, simetrikoki, pilotuek zenbat eta arinago joan, hainbat eta laburrago ikusi dituzte pistako gauzak. Horretan datza hain zuzen erlatibitatea, hots, batek bestea laburragoa dela uste du, baina bestea lehenengoa laburragoa delakoan dago, eta ez batak eta ez besteak ez du arrazoirik, edo biek dute; gauzek ez bait dute benetako itxura bakarra, baizik eta behatzailearen higidura zein denaren arabera itxura ezberdinak hartuko bait dituzte.
Eta orain dator aipatu dudan kezkatxoa: guk zertxobait gazteago ikusi ditugu pilotuak, baina haiek gu zaharrago, eta ez gazteago erlatibitatearen simetriak eskatuko lukeen bezala. Denboraren kasuan ez al da erlatibitatea betetzen? Bikien paradoxa izenaz ezagutzen da korapilo hau. Erantzuna EBTren aldekoa da. Ikus dezagun zergatia.
Hasieran, EBT azeleraziorik ez dagoen kasuetan (abiadura konstantea denean alegia) aplika daitekeela esan genuen. Pista geldirik egonda automobilak higitzen diren ala automobilak geldirik egonda pista higitzen den kontsidera dezakegu eta bata zein bestea ere zuzen daude. Beraz guk denbora automobiletan astiroago doala ikusiko dugu, eta pilotuek denbora pistan astiroago doala ikusiko dute, automobilen abiadurak konstante dirauen artean. Hemen erlatibitatearen simetria bete egiten da. Halabaina, automobilek higitzen hasita azelerazioa eta azkenean gelditzeko balaztaketa pairatu behar izaten dute.
Momentu berezi bi hauetan simetria apurtu egiten da, eta ezin dugu zein higitzen den (pista ala automobila) berdin denik esan. Haietako batek (automobilak) higidura berezia duenez gero, pilotuak badaki jakin geldirik ez dagoena. Horren ondorioa, pilotuak eta pistakoek denbora astiroago non dabilen galderari erantzuteko ados egotea da.
Ero munduan
Eta zer gehiago gertatuko litzateke hain c txikiko mundu honetan?
Goizeko 8’30etan Jone eta Mikel etxetik irten dira, 9etan Bilboko Institutuan azterketa dutelako. Biek ikasgai bat utzi egin dute bidean ikasteko. Jone Deustun bizi da. Beraz, oinez abiatu da eta gutxi gorabehera orduerdia barru heldu da, ikasgaia amaitu duelarik. Mikel, aldiz, Barakaldon bizi denez 8,30etan Abiadura Handiko Trena (29,9 km/h) hartu eta 9etan heldu da, baina ikasgaiaren hasiera ere irakurtzeko betarik ez du izan, bere tren barneko bizitzan segundo batzuk besterik ez dira igaro eta.
Halaber eta arrazoi berberengatik, oso bizitza latza ukanen lukete astronautek. Izan ere, demagun espaziuntziak 29,999 km/h abiaduraz joan litezkeela. Kasu horretan Ilargirako joan-etorriko bidaian hiru urte igaroko lirateke Lurrean, astronautaren bizitzan aste bi igaroko liratekeen bitartean (Ilargiko gainazalean egindako egonaldia barne). Bere bizitzan zehar hamabost bidaia egin ostean, bere emaztea amonatxoa eta bere seme-alabak bere adinekoak liratekeela egiaztatuko luke astronautak.
Eta guzti honetatik, azkenean zer?
Esanak esan, EBTk ez du eta ez du izango inolako eraginik ez trenetan eta ez gure bizimodu arruntean. Gainera, azaldu ditugun efektuok ez dira hitzez hitz hartu behar; hurbilpen moduan baizik. Izan ere, egunak eta urteak zeharo desberdinak lirateke c = 30 km/h-ko abiadura balego. Halaber, ikusten duzuna ez da gauzen benetako laburketa; nolabaiteko biraketa eta deformazioa baizik. Objektu baten abiadura zenbat eta handiagoa izan, hainbat eta itxura gorriagoa hartuko luke, eta abar. Baina zehaztasun guzti hauek berdin zaizkigu orain (jakinminotsuek Laburpen-ideiaren kritika izeneko koadrora jo dezakete).
Atxeki behar dugun ideia hau da: naturan abiadura maximo bat dago, argiarena, eta gertaera horrek efektu bitxi edo ezohizko batzuk sortzen ditu abiadura horretara hurbiltzen garenean. Eta nire aldetik beste ideia hau ere gehitu nahiko nuke: EBTren aztarnak sineskaitzak izan arren, guztiz ulergarriak dira. Benetan harrigarria da Einsteinen teoria zientzigizon gutxi batzuen esku soilik dagoela behin eta berriz entzutea. Arraioa! Ez gara automobil-motorea diseinatzeko gauza, baina funtzionamendu-oinarriak ulertzen ditugu. Halaxe gerta bedi EBTrekin ere!
LABURPEN-IDEIAREN KRITIKA
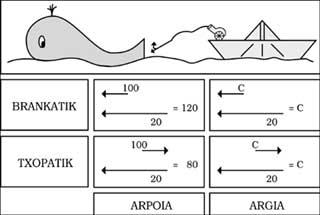
Berez honako arrazoi honegatik ezin dezakegu laburpena ikusi. Demagun v abiaduraz higitzen den A 0 B 0 D 0 E 0 gorputza dugula. Gu higiduraren norabidearekiko elkartzut gaude, B 0 D 0 aldea hurbilago dagoelarik. Dakigunez, une batean guk dakusaguna, une horretan aldiberean heltzen diren izpiak dira. Beraz, irudian ageri denez, A 0 -tik B 1 -etik eta D 1 -etik abiatutako izpiak aldiberean helduko dira gure begietaraino. Ikusiko duguna, beraz, artikuluan azaldu dugunez ez da B’D’ laburpena soilik; ezkutuan dagoen A 0 B 0 aldeko A’B’ itxura ere bai baizik. Baina ikusten dugun A’B’D’ itxura hori eta gorputza q angelua biratutakoaren irudia berdinak lirateke, irudian ikusten denez. Beraz, v abiadura c-tik hurbil dagoenean gauzak biratu egiten direla ikusten dugu eta, era berean, gauzen atzean dagoena ikusgarri suertatzen zaigu. |
Martin Axpe, Iñaki