Ciència Medieval

1989/03/01 Bandres Unanue, Luis Iturria: Elhuyar aldizkaria

• Historia

Entre ells destaca Roger Bacon. A pesar que la seva crítica era directa des del punt de vista actual però massa avançada respecte a l'ambient d'aquella època, no va tenir gran influència. En aquest aspecte és més important el XIV. realitzada a principis del segle per Duns Scoto (1265-1308). Això ho va demostrar a Oxford i París i va ampliar el camp de la teologia que l'aquiniano considerava aliena a les demostracions de la raó. La doctrina fonamental del cristianisme, segons Scoto, es basa en qualsevol voluntat divina i el do principal de l'ésser humà, molt major que la raó, era l'elecció.

Per aquest motiu, d'alguna manera, l'àmbit de la filosofia i el de la teologia s'alliberessin mútuament i la filosofia no tornés a ser la “admiració de la teologia”. Aquest alliberament suposaria el desenvolupament i la llibertat del coneixement i la introducció de l'experimentació en el camp de la filosofia va posar la base de la ciència que avui coneixem. Tanmateix, això no es va aconseguir dia a dia. XIII. A la fi del segle XIX i principis del XIV els mons de la filosofia i la teologia estaven separats entre els aquinos i els scotos.

L'entusiasta seguidor del camí emprès per Duns Scoto va ser Guillermo d'Ockham. En la seva opinió, cap resultat de la teologia podria ser provat raonadament. És més, va posar de manifest la incapacitat de la racionalitat d'algunes manifestacions que mostra l'Església. Va lluitar contra la doctrina de la supremacia del Papa i va dirigir la guerra dels franciscans contra el Papa Joan XXII. Per tot això va ser considerat com un heroi i tancat. Però després de fugir de la presó es va posar a l'abric de l'Emperador de Baviera, qui va ajudar a la llarga discussió que tenia contra el Papa.

Tomàs d'Aquino.

Ockham reconeixia les dues cares o tipus de la veritat; la veritat dogmàtica (que s'accepta a través de la fe) i la veritat filosòfica (que cal investigar a través de la raó). Aquesta actitud es va associar al renaixement del nominalisme. Segons això, l'única realitat existent és la de les coses particulars. Les idees universals, en canvi, són només noms purs o conceptes d'intel·ligència. Els aquinos o "realistes" anaven abstraient de l'universal al particular. Per contra, gràcies al ressorgiment del nominalisme, l'atenció es va centrar en els objectes que podem captar a través dels sentits i, de pas, es mirava amb total desconfiança les abstraccions. Amb el pas del temps, això suposaria una observació directa, una experimentació i una recerca per inducció.

L'Església va rebutjar i va prohibir el nou nominalisme i la Universitat de París va condemnar els escrits d'Ockham. En aquella universitat, en 1473, és a dir, durant el Renaixement, volien posar de nou el realisme com a doctrina oficial. Però les idees d'Ockham estaven completament arrelades i van seguir en elles. L'obra d'Ockham va posar fi a la prioritat de l'escolàstica medieval. Des de llavors, la filosofia no tenia per què arribar necessàriament a les conclusions que mostrava la teologia, i veient la ment lliure, va poder acudir a la recerca dels seus temes.

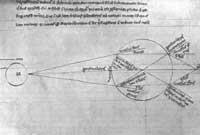
L'altre pensador que va lluitar contra l'escolàstica és Nicolás de Cusa (1401-1464). En la seva opinió, tot el coneixement humà és conjectural, encara que Déu entén tot el que s'amaga. Això és possible mitjançant la intuïció mística. Aquests cultes van portar al Cusa al panteisme. Aquest panteisme després l'assumiria Bruno. Al marge de les idees sobre el coneixement, Cusa va dur a terme la física i les matemàtiques: a través de la balança que va demostrar que les plantes prenien part del pes de l'aire en créixer, va proposar la reestructuració del calendari, es va preocupar fortament per la carrera del cercle, va defensar la teoria del gir de la Terra rebutjant el sistema de Ptolemeu. Obrint el camí a Copérnic, Bruno, amb l'astrònoma Novara, va formular la teoria que el número és l'únic absolut pel seu moviment relatiu.

Matemàtiques i Física

Si en el camp de la ciència calgués destacar un vèrtex en el camp de les Matemàtiques, l'acceptació de les xifres àrabs seria la facilitat dels càlculs que s'obtenen a través d'elles. Al principi aquestes xifres s'escrivien en “apices”, és a dir, en fitxes de branca, per a utilitzar-les en l'àbac del Gerberto (segle X). Aquestes noves xifres van ser escrites en panells recoberts de pols immediatament.

Diagrama geomètric del llibre Opus Maius de Roger Bacon.

D'aquesta manera, es podia emportar net i rectificat el que s'emportava i els resultats provisionals: XII. i XIII. Durant segles els “algorismes” demostraven aquest ús. Quan després el paper es va reduir i es va estendre el seu ús, perquè els càlculs escrits es poguessin fer sense esborrar-se, havia d'adaptar-se a la forma que utilitzem actualment. L'aritmètica era necessària en el comerç i a partir de 1340 Gènova era coneguda la comptabilitat de doble partit.

En aritmètica, juntament amb la geometria (és a dir, l'àlgebra), va començar a publicar-se l'equació secundària. Juntament amb el Fibonacci vist anteriorment, el XIV. Cal esmentar en aquest camp al mort Nicolás d'Oresme a la fi del segle XX. Això va afegir un nou nivell a la llarga cadena d'assoliments. Es deu a la suma de sèries, a les primeres bases de la geometria analítica i a la invenció dels exponents, entre altres. També es va ocupar de la dinàmica de Nicolás d'Oresme i així es va mostrar a favor del gir de la Terra, ja que “encara que els cels es mouen durant el dia i la Terra no es pot demostrar per mitjà de l'observació” és una teoria més senzilla i perfecta del gir de la Terra.

Un dels grans canvis que va suposar la matemàtica en el camp de la física va ser la teoria que totes les diferències reals podien convertir-se en diferències entre quantitats. Tal com indica Crombie, la intensitat d'una qualitat (per exemple, la calor) podia mesurar-se com la magnitud d'una quantitat. La Física Qualitativa d'Aristòtil i el XVI. La diferència entre la física matemàtica del segle XX radica en aquest canvi.

La ciència medieval va utilitzar els números àrabs per a desenvolupar l'aritmètica. Taula de punxons de moros d'argenteria de Còrdova.

XIII. A partir del segle XX la Física va sofrir un gran impuls: l'estàtica de la mà de Jordanus Nemorarius, el magnetisme amb l'aparició de la brúixola, les òptiques a l'escola d'Oxford, especialment en la Thierry de Freiberg, etc. Hauríem de tenir en compte els mitjans i la situació per a jutjar adequadament aquesta etapa de l'Edat mitjana, i potser les paraules de Beaujian ens fan:

Ptolemeu, Aristòtil i Galeno apareixien com a enormes gegants. Les seves obres estaven aixecades com a grans fortificacions. L'home de l'Edat mitjana va obrir en aquestes muralles una sèrie d'esquinçaments, però va quedar tancat en el seu interior. El futur anava a comprovar que aquí i allí, en lloc de fer una crítica o un error, el camí era tota la trituració. Calia fer una revolució: Kopernik contra Ptolemeu, Galileu contra Aristòtil i Harvey contra Galeno.