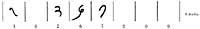Comment opérer ? (II). Multiplication et division

1990/11/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Multiplication

Quant à la multiplication, il faut mentionner un cas spécial (qui a comme produit le numéro 10). Dans le produit manuel mentionné ci-dessus, on disait que les doigts qui descendaient dans les mains se multipliaient par 10 (mentalement). A l'intérieur de cette tête est: le nombre de doigts qui descendent nous donne la dixième partie du produit.

Les Egyptiens savaient aussi multiplier par 10. Après avoir écrit un numéro, chaque symbole d'un ordre était remplacé par un symbole d'ordre suivant (figure 1).

Dans le système de numérotation chinois, vous pouvez également voir le témoin de cette affaire. Selon l'endroit où le symbole 10 est placé, vous pouvez avoir deux significations différentes (figure 2): si vous placez à gauche des symboles des autres petits nombres, vous avez la somme. Si vous écrivez à droite signifie multiplication.

Voyons comment d'autres multiplications ont été faites.

Les egypti ont écrit 1 et le plus petit produit sur le dessus de deux colonnes. Puis ces nombres étaient doublés consécutivement et écrits ci-dessous. Les doublages se faisaient jusqu'à ce que dans la colonne 1 on obtenait l'autre produit (pas le moindre) ou, si ce n'était pas le cas, jusqu'à ce que le nombre plus grand que l'autre produit apparaisse. Dans le premier cas, le résultat apparaîtrait à côté de l'autre produit, dans la colonne de droite. Dans le cas a) de la figure 3 on obtient le produit 128 x 12 = 1536. Dans le second cas, dans la colonne de gauche (colonne 1) on sélectionnait les numéros qui additionnaient le plus grand produit. Le résultat était obtenu en ajoutant dans la colonne de droite les numéros correspondants aux numéros précédents. Dans le cas b) de la figure 3 apparaît le produit 369 x 19 = 4864 + 1216 + 608 + 304 + 19 = 7011.

La multiplication egyptienne était donc implant et n'avait pas besoin de tableaux. Mais ce n'était pas la seule méthode utilisée par les Egyptiens. Ils utilisaient également la méthode appelée dédoublement. À cette occasion, les deux produits étaient écrits sur la tête de deux colonnes, calculant la moitié de la plus grande (méprisant les restes) et les doubles de la plus petite et les plaçant dans les colonnes correspondantes. Dans la colonne de paires ont été ajoutés ceux correspondants aux nombres impairs de la colonne de bas, obtenant le produit. La figure 4 montre le produit 54 x 37 = 74 + 148 + 592 + 1184 = 1998. Cette méthode apparaît également dans certains pays de l'Union soviétique.

Les Hindous utilisaient un abaque de colonne en sable. Dans cette abaque, dans la colonne de droite, écrivaient les unités; quand les dizaines étaient à sa gauche, les pourcentages à sa gauche, etc. Ils laissaient vide pour indiquer le manque d'unités (Figure 5).

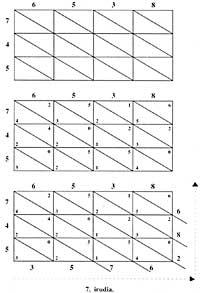
Cette abaque était utilisée pour effectuer les multiplications. Par exemple, pour calculer le produit 325 x 28, on écrivait dans un abaque à quatre colonnes, le plus grand en haut à droite et le second en bas à gauche. Dans la première étape, ils calculaient (3 ci-dessus) par (2 ci-dessous), 6 et écrivaient dans la colonne gauche du 3. Puis (3 ci-dessus) par (8 ci-dessous), 24, et au lieu de 3 écrivaient 4 et ajoutaient 2 au 6 précédent.

La première étape était terminée. Avant de commencer le second, le numéro inférieur se déplaçait par une colonne vers la droite. Maintenant (2 ci-dessus) était calculé par (2 ci-dessous), 4, et a été ajouté à la 4 ci-dessus (à gauche de la 2 supérieure). Puis (2 ci-dessus) par (8 ci-dessous), calculer et remplacer le 2 par 6, en supprimant le 2 et ajouter 1 à 8 qui était sur votre gauche. Ainsi se terminait la deuxième étape et une colonne avec le numéro inférieur vers la droite. Dans la troisième étape (5) par (2 inférieur), calculer 10; on ajoutait 0 et 6 (5 gauche) et 1 et 9 (6 gauche), le premier 6 et le second 10. Ainsi, à 8 (à gauche du 9) on y ajoutait 1, le numéro supérieur étant 9065.

Puis (5 en haut) par (8 en bas), calculer; écrire 0 au lieu de 5 et ajouter 4 à 6 (à gauche de 5) obtenir 10; écrire 0 au lieu de 6 et ajouter 1 à 0 (à gauche de 6) pour obtenir 1. Ici se terminait la troisième et dernière étape, étant le numéro supérieur 9100. C'était précisément le produit. Une note: quand nous écrivons 0 ils ont laissé la colonne vide (figure 6).

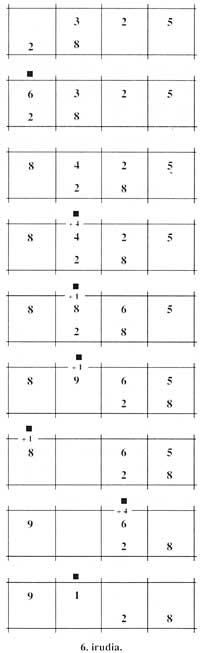
En résumé, nous pouvons écrire :

Mais cette méthode était longue et ennuyeuse. Quand ils ont trouvé le zéro, ils ont cessé d'utiliser l'abaque et les chiffres ont pris la valeur selon le lieu. Cela a facilité le calcul des opérations pour les mathématiciens hindous.

Voici comment il a été multiplié à partir du cinquième siècle. Il s'agit de la méthode dite de grille, que les Européens ont appelée per gelosia (saretazko).

Supposons que nous voulons multiplier 6358 x 547. Comme le multiplicateur 4 a 3 chiffres, dessinons un rectangle de 4 colonnes et 3 rangées. Les nombres sont écrits dans l'en-tête des colonnes et des lignes respectivement. Nous divisons chaque case par une diagonale reliant le sommet supérieur gauche au bas droit.

Dans chacune des cases, une fois multiplié les nombres dans les colonnes et dans les têtes de la rangée, ce produit étant inférieur à 100, on écrit le chiffre des dix dans la moitié inférieure et celui des unités dans la moitié supérieure; pour le manque d'unités et des dizaines on écrit 0. En dehors du rectangle et en partant du sommet supérieur droit, dans notre cas depuis le 6, on ajoute les nombres situés entre les diagonales. Si l'une de ces sommes partielles avait deux chiffres, la décimale serait ajoutée à la somme suivante et nous n'écrivions que celle des unités. Le résultat est lu de gauche à droite et de bas en haut (Figure 7).

Division Division

C'est sans lèvres l'opération la plus compliquée et comprend toutes les autres. Avant d'expliquer les divisions écrites, nous verrons une division d'il y a 46 siècles. En fait, aujourd'hui dans le village de Fara en Irak, mais dans celui de C. Le Shurupp 2650 a eu lieu dans la ville sumérienne. Bien que les chiffres sumériens existaient à cette époque, les anciens calculs étaient utilisés pour réaliser les opérations. Rappelons comment étaient les calculi:

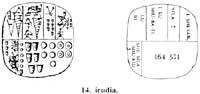
Plusieurs personnes ont partagé une grange avec 7 silas d'orge. Il fallait rechercher le nombre de personnes et le nombre d'orge restant. Une grange valait 1.152.000 silas. L'opération à effectuer était donc de 1.152.000 par 7. Tandis que le rapport nous donnerait le nombre de personnes, le sable nous donnerait l'orge restant.

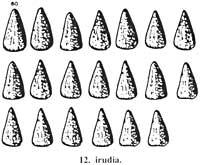
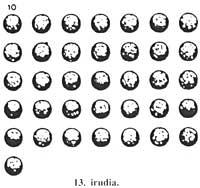
Pour représenter 1 152.000 silas, 32 billes ont été forées. En fait 32 x 36.000 = 1.152.000. Les sphères perforées ont été placées en quatre rangées de 7 colonnes (figure 9), sur quatre sphères perforées. De là, ils ont obtenu 4 x 36.000 personnes et 4 x 36.000 en excès d'orge. Les quatre sphères perforées ont été remplacées par 40 sphères (une sphère perforée avait la valeur de 10 sphères). Les 40 sphères ont été placées dans cinq rangées de sept colonnes et 5 restes de sphère (figure 10).

Donc 5 x 3600 plus et maintenant 5 x 3600 plus d'orge. En échange de cinq sphères, on obtint 30 grands cônes perforés (une sphère avait la valeur de 6 grands cônes perforés); 30 grands cônes perforés formaient quatre rangées de sept colonnes et restaient deux restes. Ils avaient 4 x 600 personnes de plus et 2 x 600 silas sans distribuer d'orge (Figure 11). Les deux grands cônes perforés ont été remplacés par 20 grands cônes (un grand cône perforé = dix grands cônes) qui ont également été placés en deux rangées de 7 colonnes, obtenant 2 x 60 de plus et laissant 6 x 60 silas non distribués (figure 12). En échange de ces dernières, 36 boules ont été prises (un grand cône = six boules) et placées en cinq rangées de sept colonnes, avec une boule excédentaire et 5 x 10 personnes supplémentaires (Figure 13). Finalement, en remplaçant la boule par dix cônes et en formant avec eux une seule rangée, c'est-à-dire un ami de plus, et en obtenant le reste final 3 silas amorcés (Figure 14). En résumé, 4 x 36.000 + 5 x 3.600 + 4 x 600 + 2 x 60 + 5 x 10 + 1 = 164.571 personnes et 3 silas orge. Une fois l'opération effectuée, le résultat était écrit dans un tableau avec des chiffres (Figure 15). Quant à la division écrite, les Egyptiens utilisaient une méthode semblable à celle utilisée dans la multiplication. 1476 divisé par 12 divisions, comme s'il s'agissait d'une multiplication, 1 et 12 en deux colonnes et au-dessous de chacune d'elles écrivaient doubles (Figure 16), jusqu'à ce que dans la colonne du 12 apparaissait le plus grand double ou le même nombre 1476. Puis, dans la colonne de droite, on marquait les numéros additionnés de 1476 et on ajoutait les numéros de la colonne de gauche à ceux qui correspondaient.

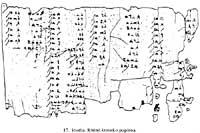
C'est-à-dire 1476 : 12 = 64 + 32 + 16 + 8 + 2 + 1 = 123. Logiquement, pour pouvoir réaliser ce type de division, la division doit être exacte. Cependant, les Egyptiens connaissaient une technique laborieuse de division inexacte. En fait, les Egyptiens connaissaient des fractions unitaires et les utilisaient pour calculer des rapports 2/n. Sur le papyrus Rhind (figure 17) apparaît un tableau de décompositions des quotients 2/n, étant n impair et de 5 à 101.

En changeant à temps, la méthode utilisée en Europe avant 1600 était la méthode de perte ou d'élimination. Ensuite, en utilisant la division 1556 : 42, nous verrons en quoi consistait la méthode :

Le succès de cette méthode est dû à la facilité d'utilisation dans l'abaque sur le sable.

XV. Au XVIIIe siècle, une nouvelle méthode de division appelée adanda est créée. Avec le mot adanda (donnant) signifie, sa cause est dans l'algorithme lui-même. En fait, lorsque le produit partiel est enlevé, le chiffre suivant est abaissé et donné au sable. Voici un exemple de l'algorithme d'adanda. Cette méthode est sans aucun doute le pionnier d'aujourd'hui.