Buscant número e
2007/11/01 Lakar Iraizoz, Oihane - Elhuyar Zientzia Iturria: Elhuyar aldizkaria
El número e és un número entre dos i tres. Si volguéssim escriure sabem que la primera xifra seria 2, després d'aquesta primera xifra hauríem de posar una coma i darrere de la coma els decimals corresponents a aquest número: 718281... Comencem a posar decimals, però acabaríem? Mai acabaríem. De fet, el número e té un nombre infinit de decimals que no tenen periodicitat, és a dir, no es repeteixen. Per això, en lloc d'expressar-se numèricament, es representa mitjançant un símbol. Igual que el número e, s'indiquen uns altres mitjançant lletres. El més famós és el número.
El matemàtic Leonhard Euler va decidir que el símbol del número e havia de ser aquesta lletra. No és molt clar per què va triar la lletra e. Han donat diverses explicacions possibles. Un sosté que Euler li va donar la primera lletra de la paraula exponencial per la forta relació entre el número e i l'exponencial. Segons altres explicacions, la va triar perquè és la primera lletra del seu cognom (idea que avui està bastant descartada), o perquè era la primera lletra de l'alfabet que no s'utilitzava en matemàtiques (les lletres a, b, c i d eren molt freqüents en les fórmules matemàtiques)... Sigui com sigui el motiu, li va donar aquest nom i des de llavors s'ha utilitzat aquest número per a expressar-lo.
Ocults en matemàtiques
Euler, a més d'apuntar-se, va fer una gran feina sobre el número e . Va definir les seves propietats cap a 1730. Davant ell va descobrir que els treballs realitzats per diversos matemàtics estaven relacionats amb el número e i es va basar en ells per a definir les propietats.
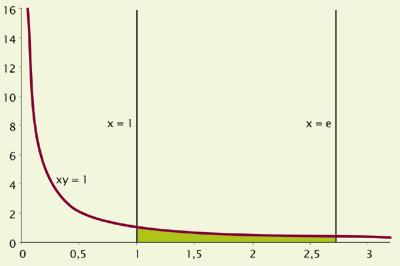
XVII. Els primers treballs es van realitzar a principis del segle XX i des de llavors alguns matemàtics, en els seus càlculs, van obtenir el número e com a resultat, però no es van adonar que tots aquests resultats eren un número únic. Per exemple, en 1661 va ser identificat per Christian Huygens. Estudiant la corba xy = 1, va voler saber entre el número 1 i l'altre número que ocupa una superfície de valor 1 (mirar la figura inferior). A aquest número li va cridar. Es tractava del número e d'Euler.
Encara que van trigar tant a descobrir i descriure, el número e és avui molt comú i utilitzat. Sol conèixer-se per primera vegada en època d'estudiant, lligat a logaritmes neperians. A partir d'aquí, alguns obliden que el número e existeix, però per a uns altres es converteix en una eina imprescindible.
Base de creixement exponencial
En alguns oficis és necessari el número e , entre altres, per a aquells que treballen amb alguna cosa que augmenta o disminueix exponencialment. Per exemple, per a mèdics forenses. Per què ? Perquè gràcies al número e, mesurant la temperatura d'un mort, poden saber quan va morir aquesta persona. Quan una persona està viva, el seu metabolisme manté constant la temperatura corporal entorn dels 36 °C. En el moment de la seva mort, el cos deixa de produir calor i el cos comença a perdre temperatura exponencialment fins a aconseguir la temperatura ambiental.
L'alta temperatura del cos en el nou mes fa que en els primers minuts disminueixi ràpidament. A mesura que es refreda, la pèrdua de calor és cada vegada més lenta. Aquesta és la particularitat del descens exponencial, és a dir, que el seu descens en un determinat període de temps depèn del seu valor a cada moment. El creixement exponencial és com el descens: quan el valor és sota, el creixement també és petit, i a mesura que augmenta, el creixement també augmenta, i a més augmenta molt!
En tot això, on està el número e ? Doncs bé, el número e és la base d'aquest peculiar ritme de creixement. Si alguna cosa té creixement exponencial, matemàticament es pot expressar amb el número e i no amb un altre número. Per tant, és imprescindible per a fer models de creixement, estimacions, previsions... d'alguna cosa. Per això és tan important.
Important i omnipresent amb creixement exponencial. Els compostos químics radioactius desapareixen al ritme marcat pel número e. Això és molt útil, per exemple, per als paleontòlegs quan volen datar alguna petjada fòssil. Mesuren el nivell de 14 isòtops de carboni radioactiu de les traces i calculen el grau de la petjada.
També les poblacions d'éssers vius (de qualsevol ésser viu, tant de bacteris com de plantes i animals), que creixen sota el número e mentre no tenen límits de creixement. Altres exemples són els que tenen un creixement exponencial sota el número e, des del creixement d'una pilota de neu en descens, fins als interessos que els bancs, o sobretot, cobren.
Més enllà del creixement exponencial
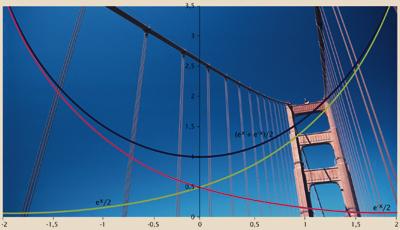
El número e també apareix en alguns casos aliens al creixement exponencial. Suposem que pengem una cadena, una corda, un cable... entre dos pals, és a dir, que tenim una catenària (com quan pengen el fil conductor per als trens o la línia elèctrica de l'electricitat). La corba de cada tram de cadena entre dos pals ve definida pel número e. La fórmula de la corba és curiosa, ja que en els seus dos sumaris apareix el número e : i = (e x + e -x )/2 . Per als enginyers que estan dissenyant aquest tipus d'estructures, per tant, el número e és un component a tenir sempre en compte. Les seves obres també depenen del número e.
No és cap número e . En el món que ens envolta apareix en més del que creem, almenys en morts, compostos radioactius, poblacions d'éssers vius, pilotes de neu, línies elèctriques, ponts penjants… i també en els diners que tenim en el banc! Encara que moltes vegades no ens adonem, si busquem trobaríem el número e en més del que pensem. És important, sens dubte.
Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia
