Unitats de temps en l'antiga Índia
La definició del temps actual (mil·lenni, any, trimestre, bimestre, mes, setmana, dia, hora, minut, segon i els seus múltiples i submúltiples) pot suposar que s'han definit amb gran precisió utilitzant conceptes i normes específiques i universals fixades de manera natural. La unitat de temps utilitzada en el sistema internacional d'unitats és de segon, i una vegada definit aquest, la resta d'unitats s'han fixat de manera única utilitzant les seves múltiples variables.
No obstant això, aquestes unitats no són les úniques unitats que poden definir-se, i pot resultar interessant observar l'existència d'una cultura en la qual la unitat de temps esmentada no s'ha definit de la mateixa manera.

Si ho hem fet (I. R. L.) En el nostre viatge a l'Índia ens va sorprendre que els hindús tenien coneixements sobre l'astronomia que els havien vingut des d'antic. L'observatori astronòmic de Jaipur ens va impressionar en gran manera, veient el conjunt d'analitzadors sorprenents que es poden utilitzar per a calcular l'hora local amb una precisió de fins a dos segons, tant la ubicació dels astres com dels planetes, quan el mesurament es realitza en un rellotge solar gegant. Diversos temes sobre els analitzadors de l'observatori “Elhuyar. Es va publicar en el número 58 de la revista “Zientzia eta Teknika”.
El que més ens va sorprendre és l'habilitat demostrada per a calcular amb precisió el temps. La sorpresa es va accentuar quan ens van donar compte que les unitats de temps utilitzades pels hindús al llarg dels anys també van anar canviant al llarg del temps. En aquest article hem decidit fer una recopilació de les unitats de temps utilitzades per aquesta cultura. També analitzarem els equivalents al sistema unitari actual i alguns derivats de les seves denominacions.
Equivalents actuals d'unitats de l'antiga Índia
No hi ha dubte que mesurar el temps de manera precisa per a la cultura de l'Índia continua tenint una importància cultural. Es creu que la importància de l'astrologia prové de la prehistòria. A mesura que les tribus s'agrupen en regnes i creixen, el seu govern es va fer més complex, augmentant el poder i la influència dels astròlegs.
Vavaha Mihiira, grans astròlegs, d. C. Qui va viure l'any 500, va afirmar en els seus escrits que a l'astròleg no li honrava que el rei era un desastre, i que un únic astròleg no podia comparar-se amb cent elefants ni amb quatre-cents cavalls.
Els coneguts d'aquests experts han aparegut en diversos llibres en els quals s'han explicat les normes precises per a dur a terme mesuraments temporals i les dades per a dur a terme alguns ritus i sacrificis. Especial importància tenien les determinacions del temps i els procediments per a calcular els detalls corresponents. Els occidentals estem acostumats a realitzar mesuraments en unitats que pertanyen a la nostra cultura i estan universalment consolidades. La determinació exacta de les unitats de temps és actualment possible i aquesta informació és útil en qualsevol punt del món. La unitat bàsica en el sistema internacional és el segon. Els 60 segons completen un minut, 60 minuts per hora i 24 hores per dia. Tenim unitats més àmplies: setmana (7 dies), mes (30 dies), any (365 dies), mil·lenni, etc.

No obstant això, les unitats esmentades no són unitats úniques i han estat modificades al llarg de la història. En el cas de l'Índia, les unitats de temps eren molt diferents. Hem decidit analitzar quines són les unitats, els seus noms i els procediments de mesurament i com van aconseguir transmetre coneixements d'un país a un altre. Per a això s'han obtingut una sèrie de dades procedents de diferents fonts que han fixat equivalents a unitats de temps i sistemes actuals.
El manuscrit més antic referenciat, el Vedanga Jiotisa, està escrit en vers amb sanscríticas, i a. C. Des de 1200 fins a 600 anys. Seguint el costum de llavors, el mestre (que era guru) ensenyava verbalment a l'alumne (que era el shishia) els coneixements que ell tenia perquè el segon aprengués de memòria. Per a facilitar el treball es van escriure en vers.
La primera unitat de temps que s'esmenta és el cicle de 5 anys (juga), que s'inicia en la Lluna del Límit (gener-febrer) i acaba en la Pausa (desembre-gener). A l'any corresponen dues parts (ayana) formades per 183 dies (savana divasa), en les quals el dia (nitemeron) és l'interval entre l'alba i el següent.
Ens referirem a les divisions de temps corresponents a intervals inferiors a la data. Referències conegudes, a. C. Són de 1200 a 1030 anys i moltes vegades no coincideixen en la manera de designar o definir la unitat de temps.
La recopilació d'aquestes dades es presenta en la següent taula.
En general, en algunes definicions podem trobar característiques comunes. S'explica a continuació. Tots tenen un temps equivalent a l'interior d'un dia o vint hores (nitemeron). El dia s'ha dividit en seixanta números (nadi, nadika, gati, gatika, danda, data), sent la unitat de temps resultant de vint minuts. Així mateix, la unitat de temps esmentada s'ha dividit en seixanta trams, aconseguint una unitat de temps de vint segons (vinadi, vinadika, pala, cashaka). Han definit com a unitats petites el temps necessari per a pronunciar la respiració, o la paraula deu síl·labes (gurvak-shara), en la qual la unitat de temps coincideix amb la sisena part de l'anteriorment definit.
Per tant, el seu valor és de quatre segons. Com a dada curiosa, es pot dir que el nombre de pantans al dia és igual al nombre de minuts en la circumferència. La relació no és tan accidental com sembla. No oblidem que la forma més utilitzada per a mesurar el temps a l'Índia era el rellotge de sol amb la projecció corresponent a l'ombra sobre el sol.
La consolidació d'unitats inferiors a quatre segons era molt difícil, entre altres coses, perquè els seus camins no eren fàcils de reconstruir. En això consisteix la diferència entre els valors de les citades unitats de temps.
Rellotges d'aigua
Els temps curts, com el prasta, es van mesurar usant rellotges mecànics d'aigua en lloc de basar-se en observacions de moviments d'estrelles com el sol. El ritual hindú només necessitava temps absolut fixat per l'astrologia i corresponent als assentaments estel·lars i planetaris. El ritu també necessitava un rellotge que regulés la successió de sacrificis. Per a complir aquest objectiu es van utilitzar rellotges d'aigua (denominats Jalaiantra).
La forma més senzilla, equivalent a la clepsida hel·lènica, era en un recipient amb aigua amb un petit forat en el fons. Recordant les paraules d'Al-Biruni:
“Llegint en el llibre Surdava d'Uptala de Kaxmirko: en la part de la fusta el buit perforat amb un diàmetre de dotze dits i una altura de sis dits té tres rages d'aigua. Si en el fons del buit es produís un forat tan gran com sis pèls de dona jove, ni anciana, ni nena, les tres mangues d'aigua caurien en un conflicte a través del forat.”
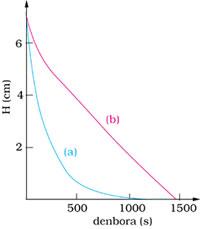
Els astròlegs actuals considerarien inadequat aquest rellotge, ja que, a part dels efectes de la tensió, el nivell de l'aigua de l'envàs va disminuint segons la següent llei exponencial:
H = H0 exp(-ct),

on c, a més del diàmetre de l'orifici, està relacionat amb altres factors, com la densitat de l'aigua i la viscositat. L'envàs es buidaria en un temps infinit. Degut a aquest efecte de la tensió superficial, el flux es talla amb un petit volum d'aigua sobre el buit.
Atès que el detall de la mesura té una dependència inversa del pendent de la corba corresponent al fluid expulsat, finalment els cronògrafs hindús haurien d'abandonar aquest procediment.
En lloc de fer l'anterior i a diferència del rellotge d'aigua egipci, en el qual el temps de caiguda del fluid es va realitzar mitjançant la lectura corresponent al nivell aconseguit per l'aigua a l'interior del recipient, l'aigua caiguda s'emmagatzemaria en un recipient de volum exacte (una prasta). En ser prasta li interessava mesurar aquest temps només per a les seves celebracions, encara que es tractava d'una unitat de volum, es va convertir en una unitat de temps. Es creu que el nivell d'aigua que hi havia en el recipient es mantindria constant i a l'altura adequada.
Aquest rellotge va millorar al llarg de la història i sembla ser que la nova versió va ser molt utilitzada en la XII. Des de principis del segle fins a l'aparició dels rellotges mecànics europeus. L'envàs utilitzat (gatis) va donar nom a l'interval de temps que va definir. Pel que sembla, el gati, equivalent a la nadika anterior i amb una durada de vint minuts, va substituir al prasta.
d. C. En la passada Suria Sidanta escrita per Ranganata cap a 1603 s'han determinat les dimensions de l'envàs: “El vaixell era una semiesfera (capala) amb una altura de sis dits (angula) i el doble d'aquesta mesura en la vora, amb una capacitat de seixanta pales d'aigua. El forat de fons era capaç de travessar una longitud de quatre dits i una agulla d'or de tres mashas i un pes d'un terç.”
Al llarg dels anys els sistemes de pes i mesura han canviat de valor i denominació, sent interessant conèixer l'equivalent a la mesura actual en cada cas. Tenint en compte que el valor de la longitud des del dit gros dels hindús fins al menor amb la mà oberta era de 22,8 cm, es pot dir que el valor de l'angula és de 1,9 cm. Una vegada calculat el volum de l'envàs es pot concloure que:
1 pala = 51,7 cc
o,
1 pala = volum = 1/2 1/4{ r360
on r = 11,4 cm.
D'altra banda, en el cas de l'antiga Varaha Mihiira, el sistema de pes es basa en la llavor de mostassa i en un gra d'arròs vuit vegades més pesat. Per a valorar la seva afirmació bàsica, 1 pala hauria de ser de 52,096 g. Segons els manuscrits, es pot deduir que la llavor de mostassa per hora tenia un pes de 3,7 mg. Sembla ser que és un valor que no ha canviat substancialment en els anys. No obstant això, la masha no es pot trobar en cap escriptura.
La velocitat de caiguda de l'aigua no té una solució analítica senzilla. L'altura de l'aigua del got de deu pales es reduirà ràpidament al llarg del temps, tal com es pot observar en la figura (b) superior, buidant-se el recipient a zero. Al final del tram, el pendent de la corba presenta un valor finit, diferent a l'obtingut en el cas de la clepsida, de manera que el detall del procediment utilitzat per a la determinació del punt final sofreixi un increment considerable. Perquè l'envàs es buidi en un conflicte, el valor d'una masha ha de ser de 0,18285 g i el canvi de pes del 0.1% variarà el resultat en setze segons.
Tornant al cas del rellotge d'aigua Surdava, mitjançant un senzill càlcul es pot deduir el valor de l'equivalent d'1 man:
1 raja = volum = 1/3\r2h3
on r = h = 11,4 cm. és. Per tant, 1 raja = 4.654 kg, és a dir, equival aproximadament a 30 pales. No obstant això, el propi Al-Biruni ha assegurat que 1 raja i 15 pales són iguals.
(1)VEDANGA JIOTIS (a. C.) 1200-600)(2)PURANA (d. C.? )(3)VISHNU PURANA (h. C. )(4) SURIA SIDANTA (<400 d. C. )(5) Col·lecció de SURIA SIDANTA (<400 d. C.. )(6) YUANG CHWANG (h. C. 629)(7) Al-BIRUNI (1030 a. C.)jugaaianasavana divasa |
6 años1 año1/2 anys(1) | (2) | (3) | (4) | (5) | (6) | (7) |
nictemero |
dia | dia | dia | dia | dia | dia | dia |
trimaiatimewatchmuhurt |
---48 min | --4 hores 48 min. | ---- | ---- |
---- | 12 hores 4 hores 48 minuts | ---- |
nadinadikagatigatikadandadata |
-24 min-- | ------ |
---24 min-24 min |
24 min24 min24 min24 min24- | ---24 min- | ------ |
--24 min- |
lavapreda |
-1min 34s | - | - | - | - |
1 min 36 seg. | - |
vinadivicalavinadikapalacashak |
----- | ----- | --24 s24 s | 24s---- | -24s - |
----- | ----24 s |
prana (respiració)asu |
- | - | 4s | 4s4s | 4s | - | 4s4s |
kastagurvakshara (silaba)tatkshanaaksharanimeshakshanahsuntruti (valor teòric) |
1,15 s--0,23 s--= 33 ?s | 3,18 s---0,21 s-- |
-2,4 s----- | ------ |
------ |
--1,6 s--0,013 skeine | ---6min |
Relació Angle/Temps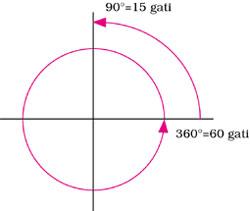 Per a dur a terme les mesures de temps a través de l'ombra del cos sobre la superfície és necessari que els astrònoms hindús coneguin les mesures utilitzades per a mesurar distàncies. En general, les ombres es projectaven sobre superfícies esfèriques (Kapala Jantra), circulars (rellotge de sol o Samrat Jantra), rodes (Txakra Jantra) o sobre un pla en el qual es representava la línia corba. En tots aquests casos, les distàncies es mesuraran en forma d'angles de circumferència o semiesfera. No obstant això, les mesures angulars no coincideixen amb els graus, minuts i segons del nostre sistema sexagesimal. Es va utilitzar el següent criteri: la circumferència es dividirà en seixanta conflictes, mentre que al gati li corresponen seixanta pales. Finalment, hi ha sis pantalons per pala (sis minuts). Així que un prán és un minut. La circumferència era l'expressió de les voltes celestes. Definint com a unitat de temps l'interval de temps que requereix l'ombra per a omplir un angle, només es pot relacionar l'angle format amb el temps emprat. Per això, en molts casos es va utilitzar la mateixa paraula per a indicar tant l'angle com el temps que li corresponia. En la següent taula es resumeixen els equivalents.
Aquesta definició era molt útil per als astrònoms hindús perquè els planetes no estan mai situats a una distància superior a 5è o 10è de l'eclíptica. A més, podien utilitzar les unitats esmentades per a situar els planetes. Coneixent les longituds i latituds corresponents als cossos celestes, el planeta podia identificar-los amb l'ajuda d'un goniometro escalonat. Podem acabar aquest apartat amb una nota important: cuidat amb les unitats en realitzar les mesures angulars amb els goniometros hindi! ! |
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian











