El tiempo juega a los dados
Desde el momento en que nacemos, el sonido tic-tac del reloj determina nuestra vida. En este viaje en el tiempo, está claro que el pasado y el futuro son radicalmente diferentes, ya que solo recordamos el pasado y no sabemos lo que vendrá después. Aunque todos sabemos esto, desde el punto de vista científico no es tan fácil explicar por qué el tiempo va siempre del pasado en dirección al futuro[1]. Pues bien, la razón es solo la probabilidad: el tiempo está jugando a juegos de azar con toda la materia del universo, como si todos fuéramos dados.
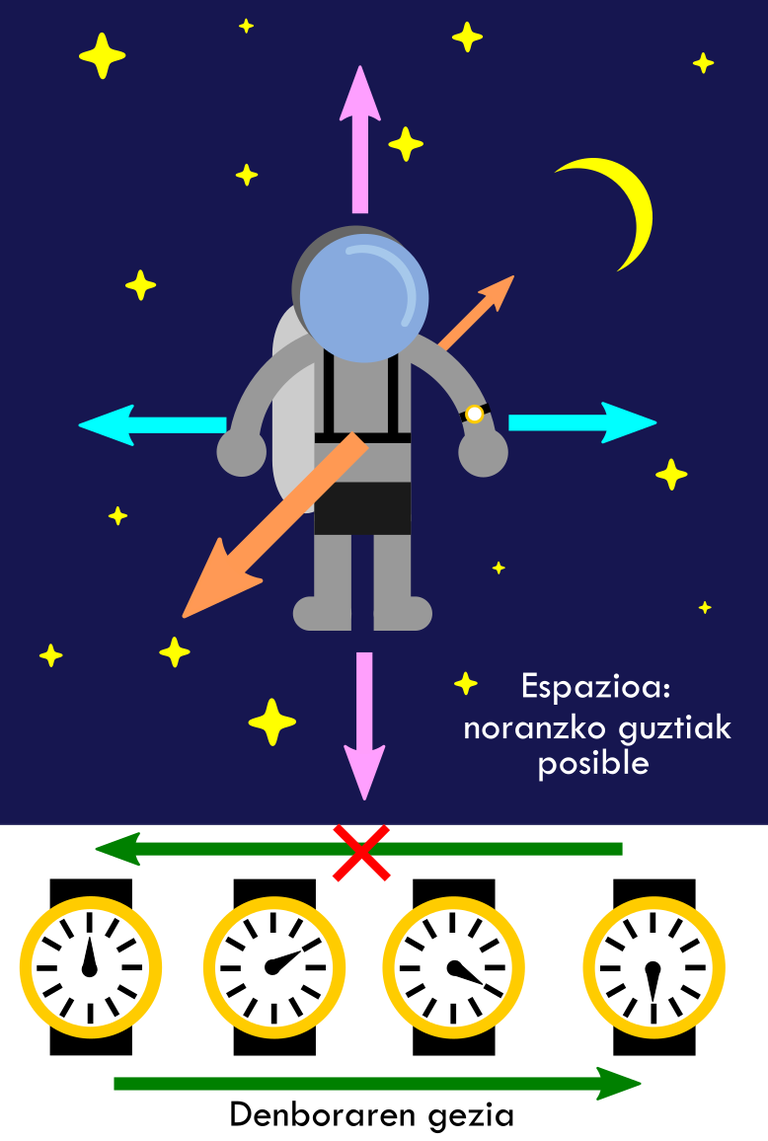
Una de las finalidades de la física es explicar el movimiento de los elementos circundantes, es decir, cómo los objetos se mueven en el espacio a medida que el tiempo cambia. En consecuencia, la física habla del espacio y del tiempo, pero la relación entre estos dos es más conflictiva de lo que parece, ya que no están al mismo nivel.
Para aclararlo, comparemos las dos magnitudes físicas mencionadas. En cuanto al espacio, tiene tres dimensiones, con dos direcciones en cada una de ellas: izquierda y derecha, por un lado; delante y detrás, por otro; arriba y abajo, por último. Desde nuestro punto de vista, ir arriba o abajo no es lo mismo, porque la gravedad nos empuja hacia abajo. Para obviar este matiz, podemos imaginar un astronauta alejado de nuestro planeta (Figura 1). Si nos encontráramos en esta situación, tendríamos ante nuestros ojos todo el universo y seríamos capaces de tomar cualquier dirección y dirección, sin ningún tipo de limitación.
El tiempo, sin embargo, solo cambia del pasado al futuro. Por lo tanto, es asimétrico en cuanto al sentido, a diferencia del espacio. Pasando a la terminología técnica, la única dirección del tiempo se denomina “flecha del tiempo”[2]. Nadie cuestiona su existencia porque todos notamos que no podemos acudir al pasado. Sin embargo, los científicos no se han conformado con aceptarlo a ciegas, y han querido ir más allá buscando la causa. ¿Por qué tiene esa flecha el tiempo?
El paso atrás o adelante en el tiempo es igual
Para responder a esta pregunta, como primer intento, lo más sensato es indagar en las leyes físicas del movimiento. De hecho, debido a las aportaciones realizadas por los físicos de antaño, es de suponer que si introducimos la mano en el cajón donde están almacenadas las ecuaciones de la física, enseguida encontraríamos la respuesta. Sorprendentemente, aunque muchas de estas leyes manejan el tiempo, la mayoría no puede explicar por qué avanza simplemente al futuro.
Uno de los pioneros de la descripción del movimiento fue Isaac Newton. De hecho, las ecuaciones que llevan su nombre indican la evolución en el tiempo de la posición de cualquier objeto. Sin embargo, sus leyes son simétricas con respecto al tiempo, en otras palabras, producen los mismos resultados en el transcurso del tiempo y en el retroceso.
Para ver esto más claramente, analicemos el ejemplo de la Figura 2 en el que lanzamos un balón de playa al aire. La trayectoria del balón es conocida para todos: partiendo hacia arriba, se ralentizará por la gravedad hasta alcanzar la máxima altura. Entonces comenzará a caer, cada vez más deprisa, y tocará el suelo (esta ruta está representada de izquierda a derecha en la imagen). Sin embargo, si retrocediéramos en el tiempo, veríamos el mismo acontecimiento (como podemos ver de derecha a izquierda): el balón irá hacia arriba, se detendrá y, finalmente, caerá. Dado que el recorrido es simétrico, no podemos distinguir los dos sentidos del tiempo.
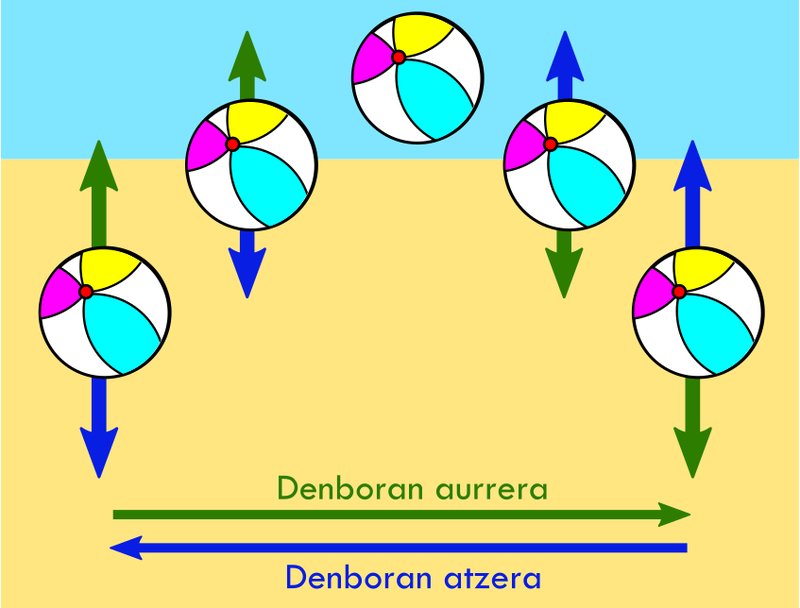
Trayectoria de un balón si lo lanzamos hacia arriba. De izquierda a derecha, recorrido en el tiempo. De derecha a izquierda, atrás en el tiempo. Debido a que ambos trayectos son totalmente simétricos, no se pueden distinguir. Ed: Unai Muniain Caballero
Aunque el del balón sea un simple ejemplo, lo mismo ocurre en muchas situaciones. En particular, el movimiento de todas las partículas que constituyen la materia es simétrico al tiempo[3, 4]; en consecuencia, su movimiento es razonable en ambos sentidos del tiempo. Esto, sin embargo, es contrario a nuestra intuición: al ver un vídeo avanzando y retrocediendo en el tiempo, la mayoría de las veces somos capaces de identificar cuál es el sentido correcto. Dado que la mayoría de las leyes de la física no son capaces de describir algo tan evidente en el día a día, tenemos que indagar más en el cajón de la ciencia para descubrir la causa de la flecha del tiempo.
De menor a mayor: la probabilidad dicta en el tiempo
El caso fue resuelto por el físico Ludwig Boltzmann, en el siglo XIX. Él obtuvo la respuesta lanzando la flecha a un campo que aparentemente no tiene relación con el tiempo: la probabilidad. La clave es el término “entropía”, que es el que fija el sentido del tiempo: solo puede avanzar en el sentido en el que la entropía sube[5].
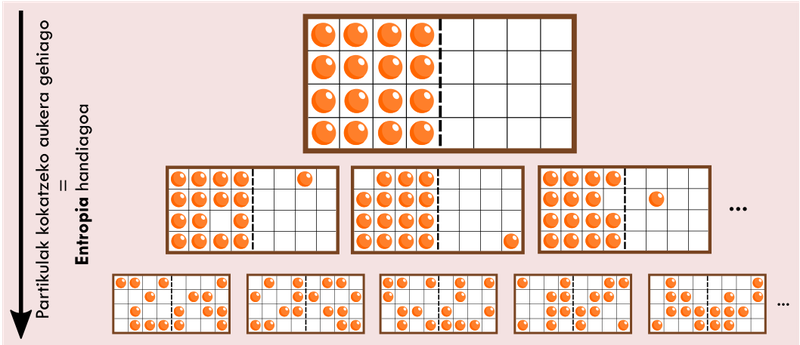
Representación gráfica de la relación entre entropía y probabilidad. Si se introducen partículas al azar en una caja, hay muchas más posibilidades de que se introduzca la misma cantidad en ambos lados que que que estén todas al mismo tiempo. Ed: Unai Muniain Caballero
La entropía a menudo se dice que es la magnitud del desorden. En cambio, el sentido del orden es subjetivo y abstracto, y en la ciencia la precisión está en el punto de mira. Por ello, profundizaremos en la definición de Boltzmann, ya que la entropía está más relacionada con la probabilidad que con el desorden[6].
Para explicar esta conexión, podemos centrarnos, para empezar, solo en la probabilidad. Supongamos que tiramos una moneda cien veces; en esta situación, es muy difícil conseguir el contrincante en todas las ocasiones, ya que basta con conseguir el reverso una vez para que tengamos la derrota. En cambio, hay muchas más posibilidades de obtener una diferencia en la mitad de las ocasiones. Así, la entropía está directamente relacionada con la probabilidad de cada evento: la segunda situación tiene mucha más entropía que la otra.
Entendiendo esto, cualquiera puede preguntarse: ¿qué relación tiene esto con el paso del tiempo? Pues bien, para ello podemos relacionar el concepto de entropía con otro estado: una caja en la que las partículas de un gas están en posición aleatoria (ver figura 3). Al igual que ocurre con la moneda, es mucho más probable que las partículas estén dispersas por toda la caja (como conseguir el contrincante y el reverso en las mitades) que todas en el mismo lado (que ver el contrincante en todas ellas), por lo que la presencia del gas en la caja tiene una gran entropía, mientras que la acumulación íntegra en el lado izquierdo es muy baja.
El hecho de que tengamos que subir la entropía explica por qué podemos captar el sentido único del tiempo. como se puede ver en la figura 4, si se vigila el movimiento de la única partícula de gas en el interior de la caja, no seríamos capaces de identificar el sentido correcto del tiempo: ambas trayectorias son posibles, tanto la anterior como la posterior, ya que la mayoría de las leyes físicas son simétricas con respecto al tiempo. Por el contrario, el paso de la mirada de pequeño a grande (es decir, no centrándonos en una sola partícula sino en todo el gas como conjunto) hace que los dos sentidos del tiempo no sean equivalentes, ya que difícilmente podemos ver el gas de toda la caja acumulándose en un lado, ya que es poco probable que todas las partículas, aleatoriamente, partan en el mismo sentido.

figura 4. Evolución del tiempo en una caja llena de gas desde el punto de vista de una partícula o del conjunto. Ed: Unai Muniain Caballero
Por esta misma razón vemos romper los vasos si caen al suelo, pero no los reparamos por sí mismos. De hecho, según las leyes de la física, es posible que las piezas rotas se junten después de la caída y se repare el vaso. Aunque esto sea posible, para ello, las moléculas de todas las partes deben coincidir tras la caída y la probabilidad es extremadamente baja: aún con los intentos repetidos, ¡para verlo tendríamos que esperar el tiempo correspondiente a la edad de varios universos!
En resumen, la asimetría del tiempo es consecuencia de la mera probabilidad: indica la tendencia de las situaciones casi improbables a las más probables. Sin embargo, como veremos a continuación, como es habitual en la ciencia, la clarificación de una cuestión plantea nuevas preguntas: aunque conocemos el sentido del tiempo, ¿qué ocurre con su inicio y su final?
El destino está escrito, pero el pasado está por escribir
Como la evolución del tiempo se basa en el aumento de la entropía, nuestro futuro lejano, que corresponde al último aliento del universo, está escrito: habrá un estado de máxima entropía al final (Figura 5). No penséis, sin embargo, que la alta entropía es apta para la vida, sino todo lo contrario. En concreto, los procesos biológicos requieren un intercambio de energía entre las células y con el medio, lo que se hace cambiando la temperatura de la materia[7]. Sin embargo, el universo de máxima entropía estaría en equilibrio térmico absoluto, es decir, todo el espacio estaría a la misma temperatura y el intercambio de energía sería imposible. Además, todos los átomos estarían mezclados formando una masa uniforme. En un universo así no habría ni seres vivos ni estrellas, por lo que este estado se denomina “muerte térmica”[8].
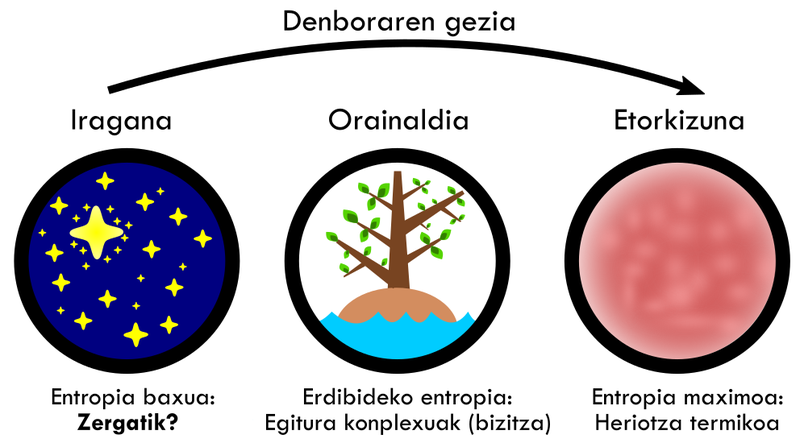
figura 5. La evolución del universo como consecuencia del aumento de la entropía. Aunque esta evolución es conocida, queda por aclarar por qué la entropía del pasado era tan pequeña. Ed: Unai Muniain Caballero
Por lo tanto, la entropía llevará al universo a la muerte. Por el contrario, en la flecha del tiempo, aunque parezca paradójico, lo que ya ha ocurrido genera muchas más dudas que lo que está por suceder.
Como ya se ha explicado, sabemos que el universo tiene hoy más entropía que ayer. Extrapolando esto hacia atrás, la conclusión es correcta: en la creación, este valor era menor que nunca. Precisamente ese es el asunto: ¿cómo es posible, desde el punto de vista de la probabilidad, que el universo comience en un estado de baja entropía? [9] De hecho, si todas las partículas del universo se distribuyeron al azar al principio, lo más probable sería que desde entonces se complete el estado de equilibrio térmico. En su lugar, la materia se situó en una situación de muy baja probabilidad: la mayor parte se concentró en varios lugares y numerosos puntos del espacio quedaron vacíos. Esta acumulación hizo posible la formación de galaxias y estrellas en diferentes lugares que han hecho posible la vida millones de años después, al menos en nuestro planeta.
Nadie sabe qué causó la baja entropía al principio del tiempo. Por esta razón, este comienzo del universo se denomina “hipótesis del pasado”[10]; sabemos que sucedió así, pero por el momento no podemos más que aceptarlo ciegamente. De hecho, gracias a la baja entropía estamos todos vivos; de no ser por eso, yo mismo no hubiera podido escribir este artículo ni leerlo vosotros. Pero así como se aclaró la causa de la dirección del tiempo, solo una investigación voluminosa podrá explicar qué causó que el universo surgiera de manera tan improbable. Mientras esto se aclara, solo podemos ayudar a elevar la entropía al universo.
Bibliografía
[1] Strogatz S. 2024. “What is the nature of time?”. Quanta Magazine.
[2] D. Layzer 1975. “The arrow of time”. Scientific American 233(6), 56-69.
[3] Roberts B.W. 2021. “Time reversal”. The Routledge Companion to Philosophy of Physics, 605-619.
[4] Albert D.Z. 2000. Time and chance. Harvard University Press.
[5] Lebowitz J.L. 1993. “Boltzmann’s entropy and time’s arrow”. Physics today 46(9), 32-38.
[6] Styer D. 2019. “Entropy as disorder: History of a misconception. The Physics Teacher 57(7), 454-458.
[7] Michaelian K. 2011. “Thermodynamic dissipation theory for the origin of life”. Earth System Dynamics 2, 37-51
[8] Adams F.C. y Laughlin G. 1997. “A dying universe: the long-term fate and evolution of astrophysical objects”. Rev. Mod. Phys. 69, 337-372.
[9] Price H. 2004. “On the origins of the arrow of time: Why there is still a puzzle about the low-entropy past”. Contemporary debates in philosophy of science, 219-239.
[10] Gryb S. 2021. “New difficulties for the past hypothesis”. Philosophy of Science 88(3), 511-532.
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian











