Fisikaren xedeetako bat da inguruko elementuen mugimendua azaltzea; hau da, argitzea objektuak nola higitzen diren espazioan denbora aldatzen joan ahala. Ondorioz, fisikak espazioa eta denbora ditu hizpide, baina bi horien arteko harremana dirudien baino gatazkatsuagoa da, ez baitaude maila berean.
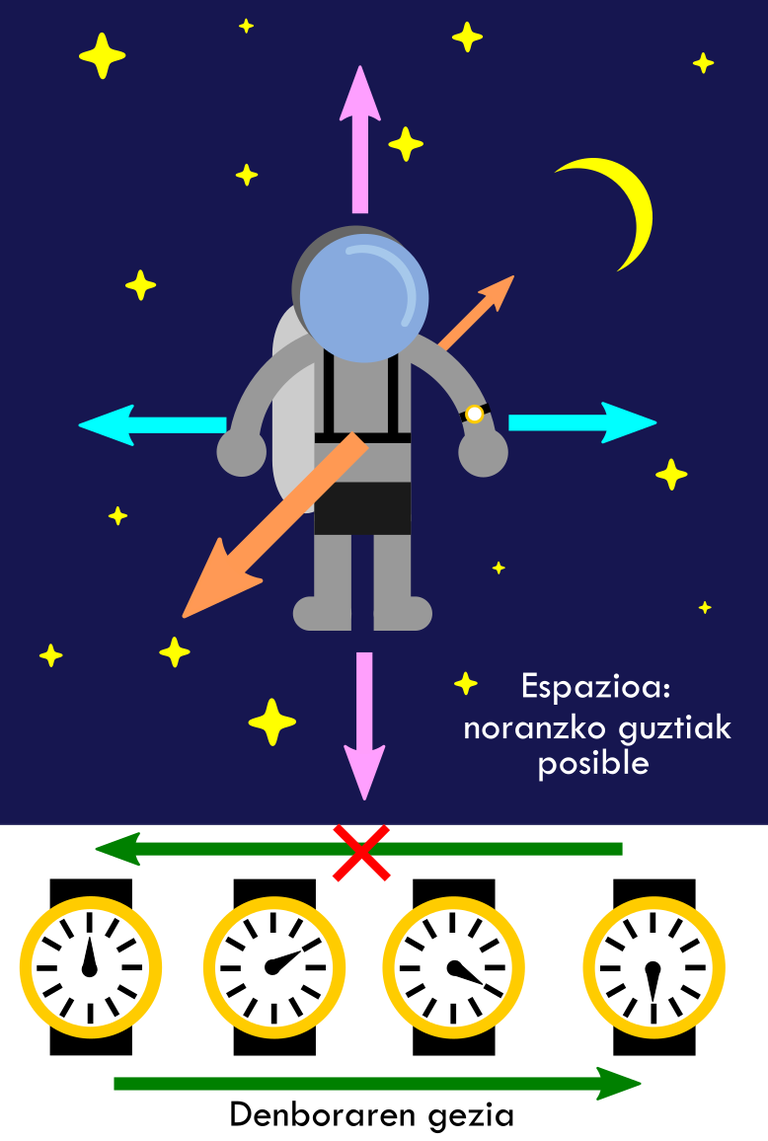
Hori argitzeko, konpara ditzagun aipatutako bi magnitude fisikoak. Espazioari dagokionez, hiru dimentsio ditu, eta bi noranzko daude horietako bakoitzean: ezkerra eta eskuina, alde batetik; aurrea eta atzea, bestetik; goia eta behea, azkenik. Gure ikuspegitik, gora edo behera joatea ez da gauza bera, grabitateak behera bultzatzen baikaitu. Ñabardura hori alboratzeko, gure planetatik urrun dagoen astronauta bat irudika dezakegu (1. irudia). Egoera horretan egongo bagina, unibertso osoa edukiko genuke gure begien aurrean, eta edozein norabide eta noranzko hartzeko gai izango ginateke, inolako mugarik gabe.
Denbora, ordea, iraganetik etorkizunera besterik ez da aldatzen. Beraz, asimetrikoa da noranzkoari dagokionez, espazioa ez bezala. Terminologia teknikora jota, denboraren noranzko bakarrari “denboraren gezia” deritzogu[2]. Inork ez du zalantzan jartzen haren existentzia, guztiok nabaritzen dugulako ezin dugula iraganera jo. Halere, zientzialariak ez dira konforme egon hori itsu-itsuan onartzearekin, eta harago joan nahi izan dute, horren zergatia bilatu nahian. Zergatik du, bada, gezi hori denborak?
Denboran atzera edo aurrera joatea berdin da
Galdera horri erantzuteko, lehen saiakera gisa, zentzuzkoena da mugimenduaren lege fisikoetan arakatzea. Izan ere, aspaldiko fisikariek egindako ekarpenen ondorioz, pentsatzekoa da fisikaren ekuazioak gordeta dauden kaxoian eskua sartuz gero, berehala aurkituko genukeela erantzuna. Harrigarria bada ere, nahiz eta horietako lege askok denbora maneiatzen duten, gehienek ezin dute azaldu zergatik egiten duen aurrera etorkizunera soilik.
Mugimenduaren deskribapenaren aitzindarietako bat Isaac Newton izan zen. Hain zuzen ere, haren izena daramaten ekuazioek adierazten dute edozein objekturen posizioak nolako bilakaera duen denboran. Hori horrela izanik ere, haren legeak denborarekiko simetrikoak dira; beste modu batera esanda, emaitza berberak ematen dituzte bai denboran aurrera joanda, baita atzera eginda ere.
Hori argiago ikusteko, azter dezagun 2. irudiko adibidea, zeinetan hondartzako baloi bat airera jaurtitzen baitugu. Baloiaren ibilbidea jakina da guztiontzat: gorantz abiatuta, mantsotu egingo da grabitatearen eraginez, altuera maximoa lortu arte. Orduan, behera erortzen hasiko da, geroz eta azkarrago, eta zorua ukituko du (ibilbide hori ezkerretik eskuinera dago adierazita irudian). Alabaina, denboran atzera joango bagina, gertaera berdina ikusiko genuke (eskuinetik ezkerrera ikus dezakegun bezala): baloia gora joango da, gelditu eta, azkenik, erori. Ibilbidea simetrikoa denez, ezin ditugu bereizi denboraren bi noranzkoak.
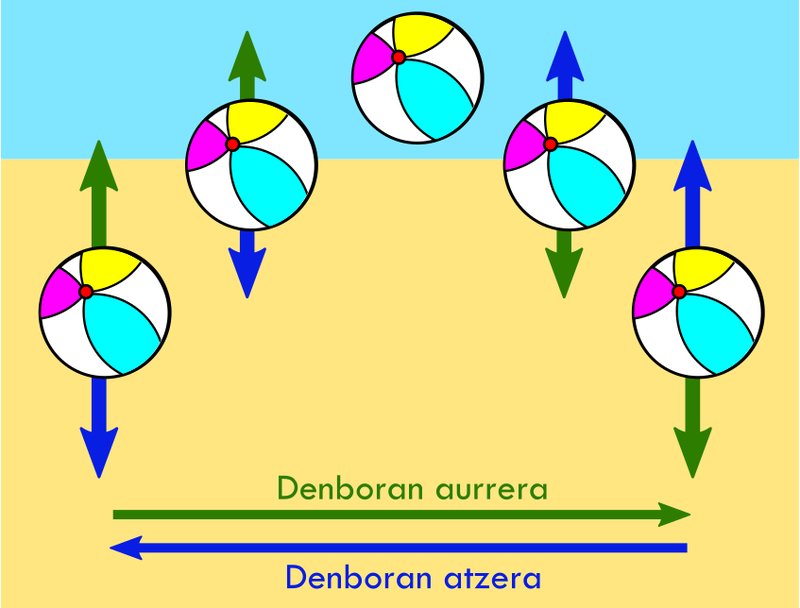
Baloi baten ibilbidea, goraka jaurtiz gero. Ezkerretik eskuinera, denboran aurrerako ibilbidea. Eskuinetik ezkerrera, denboran atzerakoa. Bi ibilbideak guztiz simetrikoak direnez, ezin dira bereizi. Arg: Unai Muniain Caballero
Baloiarena adibide soil bat izanagatik ere, egoera askotan gertatzen da berbera. Zehazki, materia osatzen duten partikula guztien mugimendua denborarekiko simetrikoa da[3, 4]; ondorioz, horien mugimendua zentzuzkoa da denboraren bi noranzkoetan. Hori, ordea, gure intuizioaren aurkakoa da: bideo bat ikustean denboran aurreraka eta atzeraka, gehienetan gai gara identifikatzeko zein den noranzko zuzena. Fisikako lege gehienak egunerokoan hain nabaria den zerbait deskribatzeko gai ez direnez, zientziaren kaxoian gehiago arakatu behar dugu denboraren geziaren zergatia aurkitzeko.
Txikitik handira: probabilitateak agintzen du denboran
Auzia Ludwig Boltzmann fisikariak argitu zuen, XIX. mendean. Hark, itxuraz denborarekin loturarik ez duen alor batera gezia jaurtita lortu zuen erantzuna: probabilitatea, hain zuzen ere. Gakoa “entropia” izeneko terminoa da, harek finkatzen baitu denboraren noranzkoa: soilik entropia igotzen den noranzkoan joan daiteke aurrera[5].
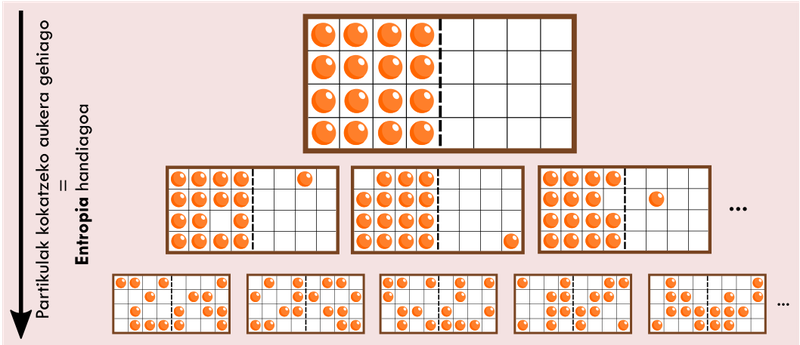
Entropiaren eta probabilitatearen arteko loturaren adierazpen grafikoa. Kutxa batean partikulak zoriz sartuz gero, askoz aukera gehiago daude bi aldeetan kopuru berdina sartzeko, guztiak aldi berean egotea baino. Arg: Unai Muniain Caballero
Entropia, askotan, desordenaren magnitudea dela esaten da. Ordenaren esanahia, ostera, subjektiboa eta abstraktua da, eta zientzian zehaztasuna dugu jomugan. Horregatik, Boltzmannen definizioan sakonduko dugu, entropiak lotura zehatzagoa baitu probabilitatearekin, desordenarekin baino[6].
Lotura hori azaltzeko, hasteko, probabilitatean soilik zentra gaitezke. Demagun txanpon bat ehun aldiz botatzen dugula; egoera horretan, oso zaila da aldi guztietan aurkia lortzea, nahikoa baita behin ifrentzua lortzea porrota izan dezagun. Aldiz, askoz aukera gehiago daude aldien erdietan alde bana lortzeko. Horrela, entropia gertaera bakoitzaren probabilitatearekin dago zuzenki lotuta: bigarren egoerak askoz entropia handiagoa du besteak baino.
Hori ulertuta, edonork egin dezake honako galdera hau: zer harreman du horrek denboraren joanarekin? Bada, horretarako, entropiaren kontzeptua beste egoera batekin lot dezakegu: kutxa bat, zeinetan gas bateko partikulak ausazko posizioan baitaude (ikusi 3. irudia). Txanponarekin gertatzen den moduan, askoz probableagoa da partikulak kutxa osoan zehar sakabanatuta egotea (erdietan aurkia eta ifrentzua lortzea bezala), guztiak alde berean egotea baino (guztietan aurkia ikustea baino); horregatik, gasa kutxan zabalduta egoteak entropia handia du, eta osorik ezkerraldean pilatzeak, ordea, oso baxua.
Entropia igo behar izateak azaltzen du zergatik atzeman dezakegun denboraren noranzko bakarra. 4. irudian ikus daitekeen bezala, kutxa barneko gasaren partikula bakarraren mugimendua zelatatuz gero, ez ginateke gai izango identifikatzeko zein den denboraren noranzko zuzena: bi ibilbideak dira posible, bai aurrerakoa, bai atzerakoa, lege fisiko gehienak denborarekiko simetrikoak baitira. Ostera, gure begiradaren jomuga txikitik handira aldatuta (hau da, partikula bakarrean zentratu beharrean gas osoa multzo bezala hartuta), denboraren bi noranzkoak ez dira baliokideak, nekez ikus baitezakegu kutxa osoko gasa alde batean pilatzen; izan ere, ez da batere probablea partikula guztiak, ausaz, noranzko berean abiatzea.

4. irudia. Denboraren bilakaera gasez betetako kutxa batean, partikula baten edo multzo osoaren ikuspegitik. Arg: Unai Muniain Caballero
Arrazoi beragatik ikusten ditugu edalontziak apurtzen lurrera jausiz gero, baina ez euren kabuz konpontzen. Izatez, fisikako legeen arabera, litekeena da pieza hautsiak erori ondoren elkartzea eta edalontzia konpontzea. Hori posible izanagatik ere, horretarako, zati guztien molekulek bat etorri behar dute erori ondoren, eta probabilitatea izugarri baxua da: saiakerak behin eta berriro eginda ere, hori ikusteko, hainbat unibertsoren adinari dagokion denbora igaro beharko genuke zain!
Laburbilduz, denboraren asimetria probabilitate hutsaren ondorioa da: ia gertagaitzak diren egoeretatik probableenerako joera adierazten du. Alabaina, jarraian ikusiko dugunez, zientzian ohikoa den bezala, auzi bat argitzeak beste galdera batzuk sortzea dakar: denboraren noranzkoa ezagutzen dugun arren, zer gertatzen da haren hasierarekin eta bukaerarekin?
Patua idatzita dago; iragana, ordea, idazteke
Denboraren eboluzioa entropia igotzean oinarritzen denez, gure etorkizun urruna, unibertsoaren azken hatsari dagokiona, idatzita dago: entropia maximoko egoera egongo da amaieran (5. irudia). Ez pentsa, halere, entropia altua bizitzarako egokia denik, guztiz aurkakoa baizik. Zehazki, prozesu biologikoek ezinbestekoa dute zelulen artean eta ingurunearekin energia trukatzea, eta hori materiaren tenperatura aldatuz egiten da[7]. Haatik, entropia maximoko unibertsoa oreka termiko absolutuan legoke; hau da, espazio osoa tenperatura berean egongo litzateke, eta energia trukatzea ezinezkoa litzateke. Gainera, atomo guztiak nahastuta egongo lirateke, masa uniforme bat osatuz. Horrelako unibertso batean ez legoke ez izaki bizidunik, ezta izarrik ere; hori dela eta, egoera horri “heriotza termiko” deitzen zaio[8].
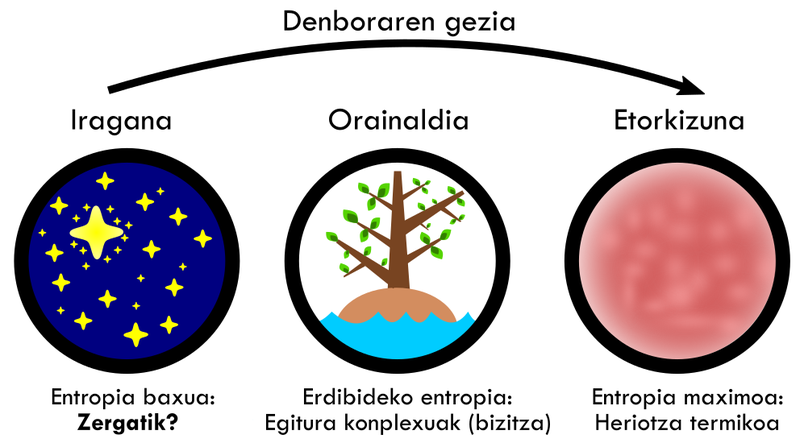
5. irudia. Unibertsoaren bilakaera, entropiaren igoeraren ondorioz. Bilakaera hori ezaguna den arren, argitzeke dago oraindik iraganeko entropia zergatik zen horren txikia. Arg: Unai Muniain Caballero
Beraz, entropiak unibertsoa heriotzara eramango du. Aitzitik, denboraren gezian, paradoxikoa dirudien arren, dagoeneko gertatu denak zalantza askoz handiagoak sortzen ditu, gertatzeke dagoenak baino.
Azaldu bezala, badakigu unibertsoak gaur atzo baino entropia handiagoa duela. Hori atzeraka estrapolatuta, ondorioa zuzena da: sorreran, balio hori inoiz baino txikiagoa zen. Hain justu, hori bera da afera: nola liteke, probabilitatearen ikuspuntutik, unibertsoa entropia txikiko egoera batean hastea?[9] Izan ere, unibertsoko partikula guztiak ausaz banatu baziren hasiera-hasieran, probableena ordutik oreka termikoko egoera osatzea litzateke. Horren ordez, materia probabilitate oso txikiko egoeran kokatu zen: gehiena zenbait lekutan pilatu zen, eta espazioko puntu ugari hutsik geratu ziren. Pilaketa horren ondorioz sortu ahal izan ziren zenbait lekutan galaxiak eta izarrak, zeinek hortik milioika urtera bizitza ahalbidetu baitute, gure planetan gutxienez.
Inork ez daki zerk sortu zuen entropia baxua denboraren hasieran. Hori dela eta, unibertsoaren hasiera horri “iraganaren hipotesia” deitzen zaio[10]; badakigu horrela gertatu zela, baina, oraingoz, ezin dugu itsuan onartu besterik. Hain zuzen, entropia baxuari esker gaude guztiok bizirik; horregatik ez balitz, nik neuk ezingo nukeen artikulu hau idatzi, ezta zuek irakurri ere. Baina denboraren noranzkoaren zergatia argitu zen bezala, ikerketa mardul batek soilik azaldu ahal izango du zerk eragin zuen unibertsoa hain modu ez-probablean sortzea. Hori argitu bitartean, unibertsoari entropia igotzen lagundu besterik ezin dugu egin.
Bibliografia
[1] Strogatz S. 2024. “What is the nature of time?”. Quanta Magazine.
[2] Layzer D. 1975. “The arrow of time”. Scientific American 233(6), 56-69.
[3] Roberts B.W. 2021. “Time reversal”. The Routledge Companion to Philosophy of Physics, 605-619.
[4] Albert D.Z. 2000. Time and chance. Harvard University Press.
[5] Lebowitz J.L. 1993. “Boltzmann’s entropy and time’s arrow”. Physics today 46(9), 32-38.
[6] Styer D. 2019. “Entropy as disorder: History of a misconception”. The Physics Teacher 57(7), 454-458.
[7] Michaelian K. 2011. “Thermodynamic dissipation theory for the origin of life”. Earth System Dynamics 2, 37-51.
[8] Adams F.C. eta Laughlin G. 1997. “A dying universe: the long-term fate and evolution of astrophysical objects”. Rev. Mod. Phys. 69, 337-372.
[9] Price H. 2004. “On the origins of the arrow of time: Why there is still a puzzle about the low-entropy past”. Contemporary debates in philosophy of science, 219-239.
[10] Gryb S. 2021. “New difficulties for the past hypothesis”. Philosophy of Science 88(3), 511-532.
Unai Muniain Caballero
Fisikan doktorea