Astronomia XVII. segle

1991/05/01 Bandres Unanue, Luis Iturria: Elhuyar aldizkaria

• Astronomia
• Historia

La teoria del moviment dels planetes ha tingut ara un desenvolupament enorme. Estem l'any 1600. Tant el Renaixement com la Reforma estan passant. En el camp de l'astronomia, alguns utilitzaven els avantatges de càlcul que oferia el sistema de Copèrnic, però sense acceptar les seves conseqüències tant físiques com filosòfiques. En aquest silenci es va escoltar una sola veu que expressava el conflicte que venia. Giordano Bruno (panteísta antiortodoxo i transeuropeu) deia que els límits de l'Univers estaven molt lluny (és a dir, en l'infinit) i que el nostre Sistema Solar és només un sistema entre altres infinits. Per totes les heretgies esmentades, la Inquisició la va jutjar i va cremar en 1600.

No obstant això, les llavors d'una nova ciència estaven germinant en qualsevol lloc. A Anglaterra Francis Bacon (1561-1626) i William Gilbert (1540-1603); en Itàlia Galileu Galilei (1564-1642); a Copenhaguen Tycho Brahe (1546-1601). És el primer home que des de l'època grega va realitzar millores en les observacions astronòmiques. Gairebé tota la seva vida, amb una precisió que fins llavors no era la mateixa, va passar a observar els moviments dels planetes. Les seves dades eren, en moltes ocasions, vint vegades més precisos que els de Copèrnic, i tot això sense inventar el telescopi.

Després de la mort de Tycho Brahe, l'alemany Johannes Kepler (1571-1630) li va donar la continuació, d'una banda fent altres observacions i per un altre realitzant una exhaustiva recerca de totes les dades preses. Mentre Tycho va desenvolupar en el seu moment un sistema planetari especial, Kepler estava a favor de Copérnic. L'objectiu dels seus treballs era fer més exactes que les taules astronòmiques dels moviments dels planetes en aquell període. Però no volia més que adaptar la teoria heliocèntrica en la base, perquè per la seva harmonia i senzillesa, la veia fascinada i a gust. Des de l'inici de les seves obres, la metafísica pitagòrica i la neoplatònica van tenir una gran influència. Aquesta tendència va seguir durant el Renaixement desafiant l'hegemonia aristotèlica.

Segons Kepler, la tendència de la intel·ligència divina era d'alguna manera geomètrica i les característiques d'aquest ordre podien trobar-se en les relacions matemàtiques que conduïen el sistema heliocèntric. Per això, en una de les seves primeres obres tractava de relacionar els sis planetes que es coneixien i les seves distàncies al Sol amb els cinc sòlids regulars de la geometria.

Quan volia adaptar les noves dades obtingudes de l'òrbita de Martitz al sistema de Copérnic i després de quatre anys de treball dur, va arribar a una conclusió molt important, que era impossible! Les noves dades situaven l'òrbita a vuit minuts de l'esquema de Copèrnic. Encara que Copérnic en el seu moment, sabent que les dades utilitzades no eren exactes, no va donar importància a aquesta diferència, Kepler sabia que les dades de Tycho eren molt més exactes que la diferència esmentada, per la qual cosa l'aconseguit era inacceptable. Per això, i amb l'honestedat que correspon als científics, no es va intentar negar les observacions i inventar noves hipòtesis per a salvar la teoria acceptada per ells mateixos. No obstant això, per a ell aquests vuit minuts indicaven: Que el sistema de Copérnic no era capaç d'expressar el moviment real de Mart. Així que va abandonar el sistema de Copèrnic amb les seves esferes concèntriques i epicicles.

Per a Kepler això seria molt dur, perquè ell era partidari del sistema de Copérnic. No obstant això, va seguir endavant i per a això va haver de trencar el jou que unia el sistema de Copèrnic amb l'antiga Grècia. Quan estudiava les trajectòries dels planetes segons la teoria heliocèntrica, se li va ocórrer que la imatge dels recorreguts podia ser de l'el·lipse (característiques de l'el·lipse a. C.). II. Eren coneguts des del segle XIX). Si s'acceptava això, és a dir, que el recorregut natural d'un planeta és el·lipse, es construïa un esquema geomètric de gran facilitat per al món. En aquest esquema, tots els planetes es mouen en òrbites el·líptiques, amb el Sol en un focus. Aquesta llei és una de les tres lleis principals de Kepler i generalment es diu que és la primera.

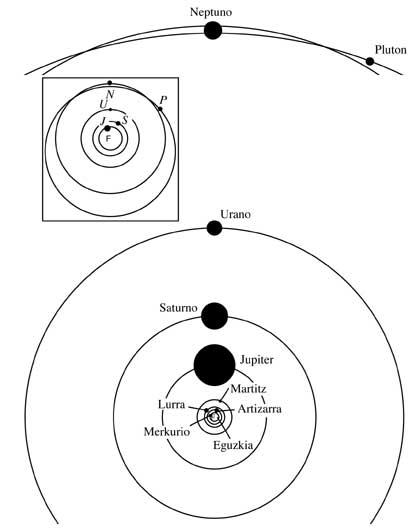
Aquesta primera llei de Kepler, en dirigir la teoria heliocèntrica de Copérnic, ens dóna una imatge molt senzilla del sistema solar. Tots els epicicles i excèntrics de Copérnic es descarten: les òrbites són només el·lipses. En la imatge es pot veure l'esquema actual i simple del sistema solar

Aquestes el·lipses són gairebé cercles i totes les òrbites es troben gairebé en el mateix pla, a excepció de Plutó. Això té una forta inclinació i tant en la imatge com en unes altres, les òrbites de Neptú i Plutó no s'humilien en cap punt de l'espai.

Probablement Kepler va ser feliç en arribar a una conclusió tan senzilla com aquesta (després de prescindir dels epicicles i excèntrics que eren molt complicats), veient que tot es complia bé a través de les el·lipses. No obstant això, en si mateixa tenia una preocupació: nosaltres podem entendre la tendència de Plató a reconèixer que els moviments circulars i uniformes eren naturals, però per què la Naturalesa tria l'el·lipse? Per a respondre correctament a aquesta pregunta cal esperar a l'arribada de Newton, que ens va dir que la llei de l'el·lipse és una conseqüència d'una altra llei de la Naturalesa molt més àmplia. Per tant, deixem el tema ara com ara.

Per això, hem de pensar que la primera llei de Kepler és un resum de les observacions realitzades, és a dir, una llei empírica. Però, encara que aquesta llei ens dóna compte de totes les localitzacions d'un planeta, no ens diu res sobre quan serà aquest planeta en l'un o l'altre lloc, és a dir, ens indica la imatge de l'òrbita, però la seva velocitat no. Per tant, aquesta llei es queda molt curta perquè els astrònoms (i Kepler també) volen saber per endavant quan serà un planeta en un punt. Per això, abans que surti la seva primera llei, Kepler tenia establerta una segona llei que ens indica els canvis en la velocitat d'un planeta.

Kepler sabia que si existís una relació matemàtica entre la velocitat d'una i una altra posició de l'òrbita d'un planeta, el sistema seria molt més senzill. Si es descobrís aquesta relació, el moviment d'un planeta es podia expressar amb molt poques dades. Es necessitaven dues dades per a proporcionar la mateixa el·lipse, el tercer per a aconseguir la velocitat en un punt concret del recorregut (en el perihelio, per exemple, el punt més pròxim al Sol) i un altre per a conèixer la inclinació del pla orbital respecte a altres planetes. Però ningú coneixia aquesta relació. Per això, quan se li va ocórrer aquesta llei es diu que estava en l'èxtasi, però el que sabem és que per a trobar-la va haver d'analitzar un munt de dades i fer un treball constant i dur.

En qualsevol cas, el camí que va seguir per a aconseguir aquesta segona llei és sorprenent, ja que sobre la base de les tres errònies hipòtesis va arribar a la seva conclusió. En paraules de Kepler, l'òrbita que descriuen els planetes es deu per força que exerceix el Sol i el valor del qual era inversament proporcional a la distància entre el Sol i el planeta. La velocitat i la força que impulsa el planeta eren directament proporcionals entre si i, per tant, inversament proporcionals a la distància. Aquesta hipòtesi (és a dir, que la velocitat sigui proporcional per força) és avui inacceptable, però es pot veure com la idea d'Aristòtil o com alguna cosa que el sentit comú donava en aquella època.

Segons aquesta hipòtesi, el temps que triga un planeta a recórrer una petita distància durant el recorregut seria proporcional a la distància al Sol. Això és gairebé totalment correcte i així en alguns punts de l'òrbita. Per tant, Kepler volia calcular el temps necessari per a completar un gran tram de recorregut (i per tant quan la distància al Sol és variable). Per a això, va tenir en compte les distàncies de tots els petits arcs que formen aquest gran tram i va concloure que aquest temps és directament proporcional a la superfície que cobreix la línia que va des del Sol fins al planeta. Segons aquesta segona llei, la Terra (o si es vol el Sol en el fons de les estrelles) s'entén que a l'hivern es mou més ràpid que a l'estiu, alguna cosa que tant Kepler com els seus predecessors coneixien perfectament.

Totes dues lleis van ser publicades en 1609 en el llibre Astronomia Nova. Però Kepler no agradava i tenia una preocupació: no es coneixia cap relació entre els moviments dels diferents planetes. Cada planeta es movia en la seva el·lipse i a la seva velocitat, però sembla que no hi havia un model general per a tots. Kepler pensava que havia d'existir aquest model general, per la qual cosa havia d'existir una relació que relacioni tots els moviments presents en el sistema solar. Kepler va partir després d'aquesta relació i per a això va utilitzar la teoria musical, segons els seguidors de Pitàgores, a la recerca d'un vincle entre les òrbites dels planetes i les notes musicals. Si la seva prolífica obra es va dir L'harmonia del món, volia expressar alguna cosa.

Creure en aquesta relació (o millor dit, la seva obsessió) pot, d'una banda, expressar la primera fe màgica dels números que tenia Kepler, però també la tendència de tots els genis de la ciència. Segons ells, la Naturalesa és uniforme i senzilla. Aquesta creença ha donat una gran ajuda als científics i una força per a superar els obstacles. Aquest és el cas de Kepler, que després de descobrir la seva tercera llei per haver sofert mil desgràcies personals, va ser capaç d'escriure:

... després d'haver trobat durant molt de temps una distància real de les òrbites utilitzant les dades de Brahe, una relació real... el fet que existeixi un consens tan ampli entre el treball que presento avui dia i el treball que jo he realitzat durant disset anys sobre les observacions de Brahe, va netejar les meves ombres de la meva ment i pensava que al principi estava en els meus somnis...

Segons el llenguatge actual d'aquesta llei, si el període d'un planeta és T (és a dir, el temps de fer un volt completa al voltant del Sol) i R el seu radi mitjà, T ² = K . R és 3, sent ^K una constant igual per a tots els planetes. En el cas de la Terra T = 1 any i R = 15 x 10 ⁷ km, per la qual cosa si coneixem el seu radi R per a qualsevol altre planeta, podem trobar el període.

Aquesta tercera llei es diu llei harmònica, perquè representa una bonica relació harmònica entre els planetes.

A través de tot això, relacionant lògicament el nostre sistema solar, el veiem com un tot simple: la nostra intel·ligència capta l'univers de Kepler amb una mirada i és capaç d'expressar matemàticament les lleis que el regeixen.

Kepler, a partir de les dades de Brahe, va intentar construir taules detallades de moviments planetaris. Per a dur a terme aquesta labor va haver d'abandonar algunes de les opinions acceptades en aquella època. Aquesta actitud era completament nova, és a dir, donar prioritat a les observacions, si aquestes es realitzaven de manera precisa i quantitativa. Un altre aspecte a destacar és la predicció de l'ús del llenguatge matemàtic en l'expressió de lleis físiques. Posteriorment, les equacions serien les expressions naturals de les lleis físiques.

D'altra banda, el moviment dels planetes en la seva òrbita en el sistema de Kepler no es considerava produït per cap déu (com ho demostraven els escolàstics), ni per les seves formes esfèriques representaven moviments circulars. En el seu últim llibre ( Mysterium Cosmographicum ) ens compta com va canviar les seves opinions en 1596:

En una època creia fermament que la força del moviment d'un planeta estava en una ànima... No obstant això, quan vaig pensar que aquesta causa del moviment disminuïa amb la distància (és a dir, com la llum del Sol disminueix amb la distància a aquest astre), vaig arribar a la conclusió que aquesta força havia de ser substancial, no literalment, sinó… com diem que la llum és una cosa substancial, és a dir, una cosa no espiritual i que sali d'un cos substancial.

En 1605 escriu a un amic:

M'he ocupat molt de la recerca de causes físiques. El meu assaig ha consistit a demostrar que la màquina celeste ha de comparar-se amb un organisme diví i no amb una obra de rellotgeria (i qui creu que un rellotge té ànima, atribueix l'honor al rellotger), i que en aquest rellotge tots els moviments diferents són el resultat d'una simple força magnètica, com tots els moviments de la màquina d'un rellotge són conseqüència d'un únic pes. A més, demostro que aquesta concepció física ha d'expressar-se mitjançant càlcul i geometria.

En Kepler podem veure clarament el canvi iniciat a Europa dos segles abans. L'observació dia a dia, els resultats, en definitiva, deixen passo a les simples especulacions i les teories han de basar-se en aquesta realitat. Per això podem dir que Kepler va fer una primera reivindicació de l'actitud moderna de la ciència.