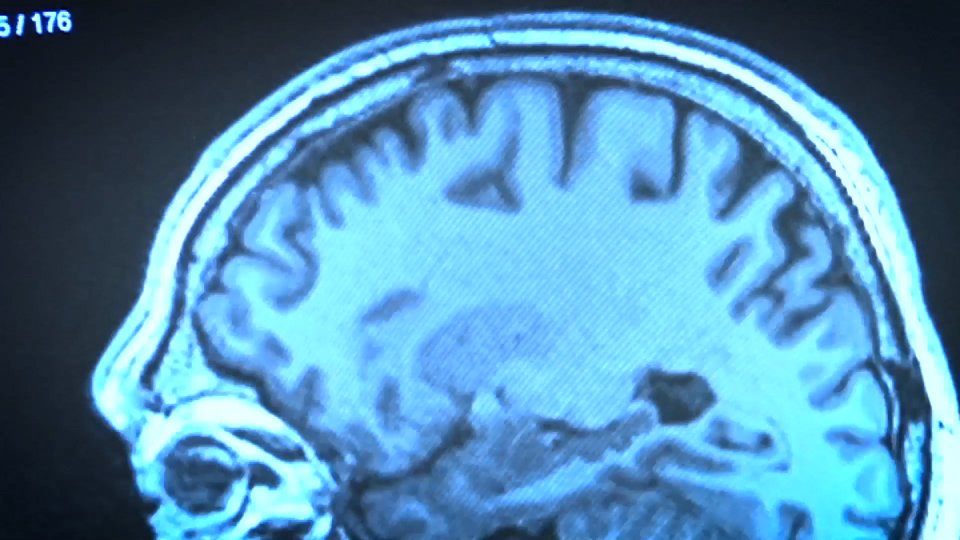
Texto redactado en euskara e traducido automaticamente por Elia e sen posterior revisión. VER ORIXINAL

Matemáticas do xabón

O matemático Anton Aubanell utiliza pompas de xabón para pronunciar discursos sobre xeometría. Tamén as utiliza na aula para dar vida ás matemáticas e sacalas do mundo limitado en dúas dimensións da lousa.

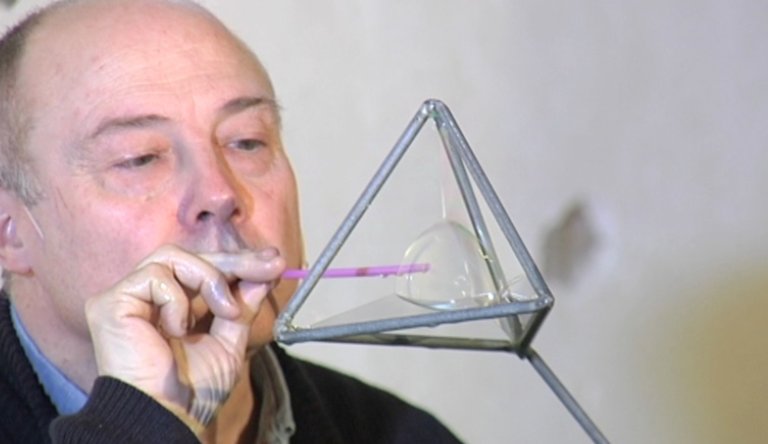
GUILLERMO ROA; Fundación elhuyar: Por que decidiches explicar as matemáticas (xeometría) a través de pompas de xabón?

ANTON AUBANELL; universidade de Barcelona: Ás veces parece que as matemáticas viven nun ecosistema bidimensional, ao que chamamos lousa. E, ao parecer, non son máis que fórmulas. No instituto empezamos a buscar unha forma de dar unha terceira dimensión ás matemáticas. Unha forma de dar vida á lousa. E atopamos lugares e contextos cheos de matemáticas. E descubrimos que a pompa de xabón é un contexto perfecto, porque é un pequeno cosmos, un mundo pequeno, moi especial e cheo de matemáticas.

ANTON AUBANELL; universidade de Barcelona: Neste mundo a beleza e as matemáticas están unidas.

ANTON AUBANELL; universidade de Barcelona: Empezamos nun instituto de Xirona, chamado Palomera, en Blanes. Eramos tres ou catro profesores e tiñamos moitas ganas de facer matemáticas máis vivas. Máis experimentos. E atopamos as burbullas.

De feito, Aubanelle converteu en pompas de xabón a escusa perfecta para falar de xeometría. As charlas son de burbullas na man. A última, a que ofreceu o grupo Lemniskata en Beasain.

ANTON AUBANELL; universidade de Barcelona: En certo xeito , as pompas de xabón aumentaran. O noso relato aumentou. Creo que as matemáticas son fascinantes e fasche moi fácil.

ANTON AUBANELL; universidade de Barcelona: Que é? Que o xabón sabe matemáticas? Sabe facer un ángulo perfecto de 120 graos? Mire: este ángulo, este e este son exactamente de 120 graos. Non é que o xabón saiba matemáticas, senón que a matemática sabe xabón. As matemáticas son unha ferramenta perfecta para interpretar o comportamento do xabón. Isto é o que os físicos chaman o efecto Mercedes. O logo é perfecto. Vemos claramente a configuración dos planos, son os planos que unen este bordo con este.Isto e isto e as dúas bases. Todas elas unidas pola superficie máis pequena. Esa é a aventura do xabón.

Con todo, a aventura do xabón rompe facilmente. Precisamente, para que as burbullas se manteñan ao máximo, Aubanelle non utiliza o xabón puro. O 60% da súa mestura é auga, o 30% xabón e o resto, glicerina, para que a auga da parede da burbulla non se evapore tan facilmente.

ANTON AUBANELL; universidade de Barcelona: Oh! Mire que bonita! Vexamos. Isto é cirurxía plástica. Mire que bonita! E que historia hai detrás desa forma. Detrás desta forma atópase a aventura de unir as doce arestas do octaedro coa superficie máis pequena. Esta fermosa forma, esta especie de diamante de tres diemnsiones, é unha forma que une os doce extremos coa superficie máis pequena. Eh?

ANTON AUBANELL; universidade de Barcelona: Non é bonito? Eu teño un xogo de sedución mutua co xabón. Non sei si podo seducir o xabón, pero o xabón sedúceme.

Estas xeometrías son moi utilizadas na arquitectura moderna para deseñar estruturas naturalmente estables

ANTON AUBANELL; universidade de Barcelona: Si queres suxeitar unhas rectas, por exemplo, a través dunha carpa, utilizando a menor cantidade posible de tea, pregunta ao xabón. O xabón pasará por estas rectas formando a menor superficie posible.

Así, por exemplo, o arquitecto Günther Behnisch deseñou o estadio olímpico de Munich para os Xogos de 1972.

ANTON AUBANELL; universidade de Barcelona: O xabón tería a mesma forma que as cubertas do estadio olímpico de Munich, si fixéseselle pasar por determinados puntos de soporte e unión. Un estudante de Xirona realizou unha maqueta do estadio olímpico nun traballo de bacharel. Fíxoo ás furtadelas, e cando se zambullía e se desjabonaba, as tapas formábanse. É dicir, o xabón facía de albanel.