The math of soap
The mathematician Anton Aubanell uses soap bubbles to give lectures on geometry. He also uses them in the classroom to give life to mathematics and to get out of the limited two-dimensional world of the blackboard.
GUILLERMO ROA; elhuyar Foundation: Why did you decide to explain mathematics (geometry) through soap bubbles?
ANTON AUBANELL; University of Barcelona: Because sometimes it seems that mathematics lives in a two-dimensional ecosystem, which we call a slate. And apparently, they're just formulas. In high school, we started looking for a way to give a third dimension to mathematics. A way to give life to the clipboard. And we found places and contexts full of mathematics. And we found that soap bubbles are the perfect context because it’s a small cosmos, a small world, very special, and full of math.
ANTON AUBANELL; University of Barcelona: In this world, beauty and mathematics are together.
ANTON AUBANELL; University of Barcelona: We started at an institute in Girona called Palomera in Blanes. We were three or four teachers and we really wanted to do some more intense mathematics. With more experiments. And we found bubbles.
In fact, Aubanell has turned soap bubbles into the perfect excuse to talk about geometry. The bubble gives the speeches in hand. The last one, which was given at the invitation of the Lemniskata group in Beasain.
ANTON AUBANELL; University of Barcelona: Somehow, the soap bubbles increased. Our story grew. I think mathematics is fascinating, and you become an amateur very easily.
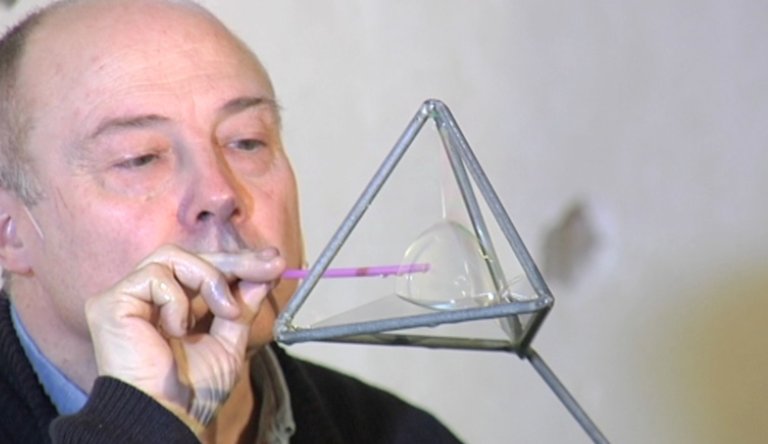
ANTON AUBANELL; University of Barcelona: What is it? That the soap knows math? can you make perfect angles of 120 degrees? Look, this angle, this angle and this angle, they're exactly 120 degrees. It's not that soap knows math, it's that math knows soap. Mathematics is an ideal tool for interpreting the behavior of soap. Physicists call this the Mercedes effect. It's the perfect logo. We clearly see the configuration of the planes; they are the planes that connect this and this edge.This and this and the two bases. All connected by the smallest surface. That's the soap adventure.
However, the soap adventure breaks down easily. In fact, in order for the bubbles to last as long as possible, Aubanell does not use pure soap. The 60% of its mixture is water, the 30% is soap, and the rest is glycerin, so that the water in the bubble wall does not evaporate so easily.
ANTON AUBANELL; University of Barcelona: Oh, that's it! Look how pretty! Let's take a look at it. That's plastic surgery. Look how pretty! What is the story behind this form? Behind this shape is the adventure of joining the twelve edges of the octahedron with the smallest surface. This beautiful shape, like a three-dim diamond, is the shape that connects the twelve edges with the smallest surface. Beautiful, huh?
ANTON AUBANELL; University of Barcelona: That's nice, isn't it? I have a game of mutual seduction with soap. I don't know if I can seduce the soap, but the soap seduces me.
These geometries are widely used to design inherently stable structures in modern architecture
ANTON AUBANELL; University of Barcelona: If you want to tie a few straights, for example, through a tent, using as little fabric as possible, ask the soap. The soap will pass through these straight lines forming the smallest possible surface.
Günther Behnisch designed the Munich Olympic Stadium for the 1972 Games.
ANTON AUBANELL; University of Barcelona: The soap would have the same shape as the covers of the Olympic stadium in Munich if we made it pass through certain support and connection points. A student from Girona made a mock-up of the Olympic stadium in a work of batchillerato. He did it with pure thread, and when he dipped it in soap and took it out, the covers were formed. I mean, the soap worked like masons.
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian











