Text redactat en basc i traduït automàticament per Elia i sense revisió posterior. MOSTRA L’ORIGINAL

Matemàtiques del sabó

El matemàtic Anton Aubanell utilitza bombolles de sabó per a pronunciar discursos sobre geometria. També les utilitza a l'aula per a donar vida a les matemàtiques i treure-les del món limitat en dues dimensions de la pissarra.

GUILLERMO ROA; Fundació elhuyar: Per què vas decidir explicar les matemàtiques (geometria) a través de bombolles de sabó?

ANTON AUBANELL; universitat de Barcelona: A vegades sembla que les matemàtiques viuen en un ecosistema bidimensional, al qual anomenem pissarra. I, pel que sembla, no són més que fórmules. En l'institut comencem a buscar una manera de donar una tercera dimensió a les matemàtiques. Una manera de donar vida a la pissarra. I trobem llocs i contextos plens de matemàtiques. I descobrim que la bombolla de sabó és un context perfecte, perquè és un petit cosmos, un món petit, molt especial i ple de matemàtiques.

ANTON AUBANELL; universitat de Barcelona: En aquest món la bellesa i les matemàtiques estan unides.

ANTON AUBANELL; universitat de Barcelona: Comencem en un institut de Girona, anomenat Palomera, a Blanes. Érem tres o quatre professors i teníem moltes ganes de fer matemàtiques més vives. Més experiments. I trobem les bombolles.

De fet, Aubanelle ha convertit en bombolles de sabó l'excusa perfecta per a parlar de geometria. Les xerrades són de bombolles a la mà. L'última, la que va oferir el grup Lemniskata en Beasain.

ANTON AUBANELL; universitat de Barcelona: En certa manera , les bombolles de sabó havien augmentat. El nostre relat va augmentar. Crec que les matemàtiques són fascinants i et fas molt fàcil.

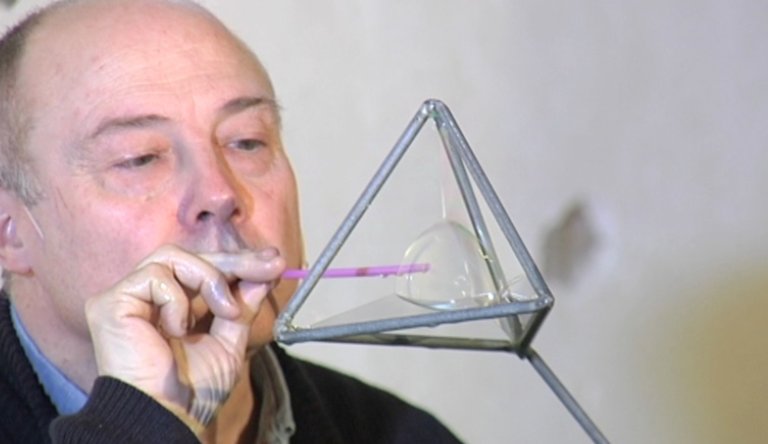
ANTON AUBANELL; universitat de Barcelona: Què és? Que el sabó sap matemàtiques? Sap fer un angle perfecte de 120 graus? Miri: aquest angle, aquest i aquest són exactament de 120 graus. No és que el sabó sàpiga matemàtiques, sinó que la matemàtica sap sabó. Les matemàtiques són una eina perfecta per a interpretar el comportament del sabó. Això és el que els físics diuen l'efecte Mercedes. El logo és perfecte. Veiem clarament la configuració dels plans, són els plans que uneixen aquesta vora amb aquest.Això i això i les dues bases. Totes elles unides per la superfície més petita. Aquesta és l'aventura del sabó.

No obstant això, l'aventura del sabó es trenca fàcilment. Precisament, perquè les bombolles es mantinguin al màxim, Aubanelle no utilitza el sabó pur. El 60% de la seva mescla és aigua, el 30% sabó i la resta, glicerina, perquè l'aigua de la paret de la bombolla no s'evapori tan fàcilment.

ANTON AUBANELL; universitat de Barcelona: Oh! Miri que bonica! Vegem. Això és cirurgia plàstica. Miri que bonica! I quina història hi ha darrere d'aquesta forma. Darrere d'aquesta manera es troba l'aventura d'unir les dotze arestes de l'octaedre amb la superfície més petita. Aquesta bella forma, aquesta espècie de diamant de tres diemnsiones, és una forma que uneix els dotze extrems amb la superfície més petita. Eh?

ANTON AUBANELL; universitat de Barcelona: No és bonic? Jo tinc un joc de seducció mútua amb el sabó. No sé si puc seduir el sabó, però el sabó em sedueix.

Aquestes geometries són molt utilitzades en l'arquitectura moderna per a dissenyar estructures naturalment estables

ANTON AUBANELL; universitat de Barcelona: Si vols subjectar unes rectes, per exemple, a través d'una carpa, utilitzant la menor quantitat possible de tela, pregunta al sabó. El sabó passarà per aquestes rectes formant la menor superfície possible.

Així, per exemple, l'arquitecte Günther Behnisch va dissenyar l'estadi olímpic de Munic per als Jocs de 1972.

ANTON AUBANELL; universitat de Barcelona: El sabó tindria la mateixa forma que les cobertes de l'estadi olímpic de Munic, si se li fes passar per determinats punts de suport i unió. Un estudiant de Girona va realitzar una maqueta de l'estadi olímpic en un treball de batxiller. Ho va fer d'amagatotis, i quan es capbussava i es desjabonaba, les tapes es formaven. És a dir, el sabó feia de paleta.