Limite des trous noirs dans les environs (I)

1993/04/01 Arregi Bengoa, Jesus Iturria: Elhuyar aldizkaria

• Astrofisika

Le fait que pour décrire les trous noirs leur masse, le moment angulaire, et peut-être seulement besoin de charge, peut nous conduire à les considérer dans une certaine mesure comme un objet simple. En tout cas, l'image des trous noirs, qui sont des objets invisibles parce qu'ils absorbent tout autour de vous et ne laissent pas échapper la lumière, est trop simple. Ensuite, nous allons essayer de compléter un peu cette image en analysant la structure des trous noirs. A cette occasion, nous nous limitons à ceux sans mouvement de rotation.

Selon l'image des trous noirs statiques que nous donne la théorie de la relativité générale, ceux-ci sont sphériques, mais la matière ingérant ne répond pas au volume total correspondant au rayon de Schuwarschils. Le rayon de Schwarzschill est considéré comme la limite du trou noir, car la matière qui tombe dans la sphère définie par lui ne peut pas en sortir, mais cette sphère n'est pas pleine de matière et n'a pas la surface aussi compacte qu'une étoile à neutrons ou une planète.

La coquille imaginaire qui définit le rayon de Schwarzshild est souvent appelée l'horizon des faits et, comme nous l'avons dit, n'est qu'une limite. La matière qui la traverse ne subit aucun effet spécial. Une fois passé l'horizon des faits, la matière suit son voyage et tout s'accumule au centre de la sphère dans un point de densité infinie. Bien sûr, ce type de points génère de gros casseroles de tête aux scientifiques et a été mis un nom spécial: le point singulier. Cependant, nous en parlerons à la fin, car nous devons éclaircir un peu la nature de l'horizon des premiers événements. Pour cela, nous suivrons un hypothétique astronaute dans son voyage jusqu'à nous plonger dans le trou noir.

Comme on le sait, la théorie de la relativité générale ne décrit pas la gravité comme force qui se transmet sans contact. Dans la théorie d'Einstein l'espace et le temps forment un tout unique et la gravité est le résultat de la déformation qui produit la masse dans la géométrie spatio-temporelle de son environnement. L'espace/temps vide sans masse est totalement plat, mais s'il y a matière, la géométrie de l'espace/temps s'incline et cette inclinaison ou courbure est celle qui déplace les masses.

Comme la courbure spatio-temporelle diminue avec la distance, l'influence sur les régions éloignées du trou noir est faible ou presque nulle. Par conséquent, notre astronaute n'aurait aucun problème dans ces régions pour se déplacer librement. Au contraire, plus le trou noir est proche, plus la puissance devrait utiliser les moteurs de l'espace si vous ne voulez pas rester immobile ou tomber dans un endroit. Cependant, la puissance élevée du moteur ne nous dérange pas, parce que notre voyage a un trou noir cible. Cependant, si vous voulez voyager et parcourir le trou noir, l'astronaute devrait bien penser aux trous noirs qui entourent votre espace. Vous devriez choisir un grand trou noir. Sinon, la force de marée créée par le trou noir détruirait l'espace et son contenu. Mais nous allons expliquer ce problème plus lentement.

Comme on le sait, la force de la gravité diminue en fonction de la distance à la masse qui la produit. Dans le cas des astres de moindre masse comme la Terre ou la Lune, les effets de cette dépendance de la distance de force ne sont pas très violents, mais du tout méprisables. Par exemple, les marées provoquées par la Lune sur Terre sont dues au fait que la force d'attraction de la Lune est plus grande que celle opposée à la Terre qui regarde notre satellite. Si on considère que l'astronaute est debout dans l'espace, la force que le trou noir attirera les jambes sera plus grande que celle qui attire la tête.

Sur le sol comme sur les astres de masse et de densité d'étoiles, bien que cette différence à quelques mètres est totalement négligeable, dans le cas des trous noirs peut être suffisant pour allonger et broyer l'astronaute comme un spaghetti. Par exemple, pensons que le corps humain ne peut supporter des tensions ou des pressions 100 fois supérieures à la pression atmosphérique normale. Dans ce cas, dans le trou noir de 10 ms, dont le rayon serait de 30 km, l'astronaute mourrait 400 km au-dessus de l'horizon des événements.

Cependant, l'intensité des forces maréales dépend de la densité de la matière qui les produit. Étant le trou noir le plus massif, la densité est inférieure, la géométrie de l'espace/du temps se courbe moins et les forces maréales seront mineures. Par exemple, l'astronaute n'aurait aucun problème à traverser l'horizon d'un trou noir de 1000 ms.

Après avoir analysé le point de vue de l'astronaute, nous essaierons ensuite de répondre à une nouvelle question : Comment verrions-nous si ce transit de la Terre contrôlerait le vol spatial ? Pour répondre à cette question, nous devons garder à l'esprit que, selon la théorie de la relativité générale, le temps ne passe pas la même chose pour deux observateurs qui se déplacent avec accélération relative. Par conséquent, le temps de médiation de l'astronome ne serait pas le même que celui qui se mesurerait sur Terre.

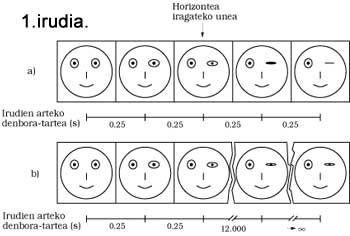
Le temps mesuré par l'observateur qui vit l'événement que nous voulons analyser est appelé temps propre et temps apparent aux autres. Par exemple, le temps qui mesure le temps apparent entre deux phénomènes est toujours plus long que celui qui est mesuré en temps propre ; plus l'accélération relative est longue. Ainsi, en passant l'horizon des événements, en déplaçant l'espace avec une accélération très élevée, même si les intervalles de temps mesurés par l'astronome sont finis, ceux qui seraient mesurés dans le temps apparent augmenteraient indéfiniment. Pour mieux comprendre ce que l'on veut dire, pensons que nous avons parlé à l'astronome pour qu'il nous fasse un geste en passant l'horizon des faits.

Dans la section a) de la figure 1, vous pouvez voir comment une caméra dans l'espace enregistrerait le geste. Comme on le voit, la troisième photo correspond à l'étape et rien de spécial n'arrive. Dans la section b) on peut voir comment nous recevrions l'enregistrement sur Terre, c'est-à-dire les images que nous recevrions en mesurant les mêmes intervalles apparents. Au début, ce que nous verrions sur notre écran et les séquences de l'alinéa a) seraient les mêmes, mais à mesure que l'espace s'approche de l'horizon, les images que nous recevrions dans les mêmes intervalles de temps seraient presque égales, puisque l'astronaute nous enseignerait le moment où l'horizon traverse. D'une certaine façon, le temps et les images sont gelés. Les deux photos après l'horizon n'arriveraient jamais, bien sûr, parce que du trou noir on ne peut rien retirer. Autrement dit, les images qui sortent du contour du trou noir, ou enfin les radiations, sont obtenues à une fréquence de plus en plus apparente. Par conséquent, le rayonnement se déplace vers le rouge, perd de l'énergie et l'intensité de l'image devient de plus en plus faible.

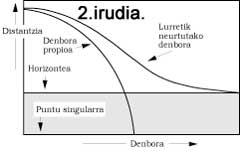
La courbe “Temps mesuré depuis la terre” de la figure 2 nous indique aussi ce que nous venons d’expliquer. L'autre courbe représente le temps propre et, comme on le voit, elle ne connaît aucun changement, même après s'être mise dans le trou noir (représenté par rayé dans l'image). On observe que le voyage indispensable jusqu'à la singularité se produit aussi dans un temps propre fini. Par exemple, pour un trou noir de 10 ms, ce temps serait juste une famine de seconde, et pour celui qui se formerait dans le noyau d'une galaxie serait également d'une heure. Cependant, quand nous parlons de questions dans les trous noirs, nous devons garder à l'esprit que le point singulier qui prédit la théorie de la relativité générale est un point très spécial et incompréhensible où notre théorie perd toute sa capacité à décrire ce qu'elle prédit ou une situation. Pour cette raison, beaucoup considèrent que la dynamique dans le trou noir ne peut être étudiée avec une base minimale tandis que la théorie d'Einstein ne se développe pas en tenant compte des principes de la mécanique quantique, c'est-à-dire tant que la gravitation quantique n'est pas développée.

ÉPHÉMÉRIDES SOLEIL: 20 avril, 1 h 49 min (UT) entre dans le Taureau. LUNE: PLEINE LUNE QUATRIÈME MENGUANTE NOUVELLE LUNE QUART CROISSANT jour (UT) 618 h 43 min. 1319h 39 min 2123 h 49 min. 2912 h 40 min PLANÈTES MERCURE: la première semaine passera par son allongement maximum. Par conséquent, ces jours sont les mieux adaptés pour voir Mercure à l'aube. Cependant, cette allongement maximale n'est pas très appropriée. VÉNUS: Il est en conjonction un jour, il est donc invisible. Au cours de la deuxième quinzaine, nous pourrons la voir le matin. MARTITZ: au crépuscule apparaît haut dans le ciel et ne disparaît pas à l'horizon Ouest jusqu'à 1h (UT). Cependant, leur ampleur diminue. JUPITER: L'opposition vient de passer et vous pouvez voir toute la nuit. Au crépuscule, il est visible et traverse le ciel pendant la nuit. SATURNE: apparaît au petit matin une demi-heure avant la première lumière de l'aube et chaque jour avant.