Historia das cifras (V)

1990/09/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Despregamento do novo sistema

O sistema hindú tardou mil anos en chegar até Europa, onde os árabes foron mediadores.

A expansión árabe (VIII-XIII. Durante o século XIX, todos os pobos reuniron obras gregas, filosóficas, científicas ou literarias e as arabicaron. En todos os lugares creáronse bibliotecas e universidades. Bagdad, Damas e máis tarde as cidades de Alkairo, Kairuan, Fes, Selecta e Córdoba convertéronse inmediatamente en centros científicos.

En Europa XI. Até o século XX viviuse una crise política e científica. Por exemplo, paira ensinar aritmética teórica, o Nicomaco de Geresa (d.C.) II. século XX), inspirado por unha obra matemática frouxa do grego Boecio (d.C.) No século V utilizábase una obra que se atribuía ao latino. En canto á aritmética práctica, manexaban a numeración romana e o ábaco.

Os árabes, ao principio, asimilaron a numeración alfabética grega e hebrana e adaptárona ao alfabeto dos seus 28 letras. Doutra banda, recuperouse o sistema de posición sexagesimal e o cero dos babilonios. Pero cando coñeceron o sistema hindú a través das relacións comerciais, fixérono na súa totalidade.

Os árabes non quedaron niso e achegaron á cultura. Á hora de recompilar e traducir os traballos antigos fixéronse algúns comentarios. Ademais, a rixidez de sistematización dos matemáticos gregos asociouse á practicidad da ciencia hindú.

Entre os matemáticos árabe-islámicos destaca o samanés Mohamed Ibn Mussa ao-Khowarizmi (780-850). É coñecido polos seus dous libros. Na primeira fálase de aritmética e nela explícase o sistema hindú con exemplos. Posteriormente abriríase con éxito na Europa occidental. De feito, o nome latino do autor converteuse no sinónimo do sistema. No seu segundo traballo tratou a ciencia algebraica. Tamén foi famoso. O título deste traballo comezaba coa palabra alj. Una das dúas operacións que cambiaban de sección os termos paira deixar termos positivos en dous partes dunha ecuación chámase:

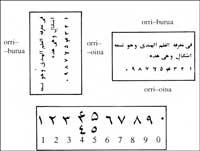
Cando os árabes conquistaron o sistema hindú, non fixeron máis que copiar as cifras. Despois de pasar polas mans dos copistas cambiaron de aspecto.

Un motivo de cambio aparente atópase na escritura, xa que escribían por columnas, de esquerda a dereita. Dábanlle un xiro de 90° paira ler, no sentido das agullas do reloxo. Con todo, foron cifras que se difundiron polas provincias árabes e que eles chamaban “hindi”.

Pero as nosas cifras non proceden directamente destas, senón das dos árabes occidentais. IX. No século XVIII rompeu o imperio árabe-musulmán, quedando fose do califato de Bagdad o África noroccidental e a rexión musulmá da Península Ibérica. Con todo, as relacións non romperon, sobre todo por peregrinacións até A Meca, intercambios comerciais, guerras e migracións de poboación. Os árabes orientais ensinaron aos occidentais o sistema hindú. Nesta rexión as cifras evolucionaron de maneira diferente.

Estas cifras denominábanse “ghobares” (cifras en po) polo po que se esparcía paira poder escribir as cifras nas táboas de cálculo. Este cambio aparente débese á forma gráfica dos copistas occidentais.

Mentres os árabes coñeceron o sistema hindú, tiveron que pasar séculos para que os europeos aceptáseno. Na Europa da época, desde a abolición do Imperio romano até o final da Idade Media, o cálculo (cálculo por ábaco) estaba en mans de privilexiados. Con todo, os occidentais podían obter as vantaxes do sistema hindú grazas ao monxe Gerbet d’Aurillac, que no ano 999 foi nomeado Papa Silbestre II. No convento Gerbert estudara matemáticas e astronomía. Durante a súa estancia na Península Ibérica estudou o sistema de numeración e métodos de cálculo dos árabes. Como director da escola diocesana de Reims tentou aplicar os seus estudos. Pero, desgraciadamente, só logrou introducir cifras (salvo cero). Nos ábacos de columna substituíronse os cantos por cifras, pero naqueles ábacos non era necesario o cero.

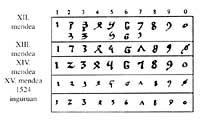
Do mesmo xeito que ocorreu cos árabes, en Europa as cifras se distorsionaron por diferentes motivos; por escribir de fantasía, por copialas boca abaixo ou indirectamente, etc.

Tras o paso das cruces recuperáronse as grafías orixinais. XIII. e XIV. A partir dos séculos XVI converteuse na imaxe actual. A imprenta de Gutenberg fixou paira sempre as formas das cifras. Aínda que o obxectivo das cruzadas non era a reconquista da ciencia e a cultura, foi un dos resultados. Os cruzados que se dirixiron a Terra Santa regresaron coa cultura local. Os cruzados tiveron intercambios comerciais e culturais cos musulmáns. Grazas a eles o sistema hindú penetrouse en Europa.

Alén do mar Mediterráneo, na Península Ibérica, XI. Desde finais do século XX os intercambios culturais fortalecéronse grazas ás obras dos tradutores. Entón os cristiáns empezaron a traducir todos os traballos ao latín.

Nese ambiente destacou un matemático italiano: Leonardo de Pisa, chamado “Fibonacci”. Estudou o sistema árabe en África musulmá e Oriente Próximo. Posteriormente, no ano 1202, presentou o traballo Liber Abaci (Tratado de Abaco), no que explicaba as regras do cálculo de cifras. A partir de agora os afeccionados ao novo cálculo multiplicáronse. Con todo, o desenvolvemento estaba lonxe.

Había dúas razóns principais para que non se aprobase o novo cálculo. Por unha banda, os “donos” do antigo cálculo vían perigar a súa vida. Por outra banda, existía a Igrexa, que pediu que o desenvolvemento da ciencia dependera das súas dogmas. A facilidade de cálculo dos árabes foi acusada a Satanás.

Tamén nos axudará a etimología de cero e cifras. A palabra cero provén da palabra sanscrítica sifr (hutsa, hinduen sunya). Fibonacci, que na súa obra Liber Abaci chamoulle zephirum, máis tarde converteuse en cefiro e a partir de 1491 quedou cero. Pero da palabra sifr tamén vén a palabra cifra. As súas transcricións en latín Sifra, Cifra, Cyfra, Tzyphra, Cifre, Cyfre, etc. son. Nun principio esta palabra tivo o significado de cero. Paira entendelo hai que volver ao ambiente que marca a Igrexa. O uso de cifras árabes estivo prohibido no seu día. Doutra banda, a xente utilizaba o sistema oculto e empezou a denominarse “cifra”, mesturando ambos os significados (cero e cifra). Os expertos trataron de manter o seu significado orixinal, pero non o conseguiron.

Os científicos mostráronse inmediatamente a favor do novo sistema. Aos comerciantes, banqueiros, funcionarios e en xeral atrasados custoulles moito abandonar o ábaco. Situación durante a Idade Media e o Renacemento XVII. e XVIII. Mantívose nas administracións até os séculos 20.

Acabouse?

Finalmente e tras unha longa historia de obstáculos, o noso sistema completouse. Pero terminou a historia das cifras? Polo menos así o creemos. A pesar de cambiar a grafía das cifras cando aparecen os computadores, o seu nome non se moveu. Poderiamos pensar noutras bases como as 12 ou 2 (as dos computadores). Con todo, o sistema non cambiaría. Subsistirían o principio de posición, o cero e as regras de cálculo.

Desde a época do home Crô-Magnon até o home moderno non houbo cambios básicos no cerebro, senón riqueza cultural. O matemático Leopoldo Kronecker dixo: “Deus creou o número natural, o resto obra humana”. Ou en palabras do filósofo alemán Lichtenberg: “O home empezou desde o principio: toda magnitude é igual a si mesmo, e chegou a medir o Sol e as estrelas”.

A teoría da visita de seres doutros mundos fallou neste campo. Si eran tan rápidos, por que non nos deixaron a numeración de posición e o cero?

En cifras non hai torre de Babel. Mentres en todo o mundo hai máis de catro mil linguas e decenas de alfabetos, na actualidade todos os pobos aceptaron o sistema de cifras hindú.

Este sistema permitiu a creación e desenvolvemento de calculadoras e tratamento da información. Isto non fose posible con outros sistemas. Ao principio Leonardo de Vinci, Pascal, Leibniz, Babbage,... (mecánica) máis tarde Hallerith, Torres Quevedo, Arken,... (electromecánica) e finalmente Turing, Atanasoff, Von Neumann,... Isto débese ao labor realizado polos científicos (electrónica).

Xunto ás cifras desenvolveuse o concepto numérico e a escritura matemática.

Durante moito tempo non se podían escribir números negativos, nin tampouco remisións como 4 - 7. O concepto cero deu esa oportunidade.

Outro logro foi definir e unir conceptos diferentes. Por exemplo, as fraccións. Coñécense desde a antigüidade. Os egypti só coñecían as fraccións orixinais (cando o numerador é 1). Os babilonios deron ás fraccións una redacción racional, creando fraccións sexagesimales. Os gregos, ante a imposibilidade da súa numeración alfabética, adoptaron o sistema babilónico. A escritura moderna débese aos hindús e a invención da liña aos árabes.

Posteriormente, o descubrimento das fraccións decimais (cando o divisor é a reversión decimal) permitiu escribir cifras á dereita de cómaa. En Europa, o primeiro foi o belga Simón Stevin, que escribiu en 1582 713 (0) 7 (1) 9 (2) 4 (3) paira escribir o número 713,794. Dez anos despois o suízo Jost Bürgi escribiu 713 794. Ese mesmo ano o italiano Magini substituíu a circunferencia por un punto por 713.794. E en canto a cómaa de hoxe, o neerlandés Wilbord Snellius inventou o XVII. principios do século: 713,794. A racionalización da escritura das fraccións facilitou a invención do sistema decimal de medición.

a.C. VIN. Antes do século XX os matemáticos gregos coñecían a existencia dos números irracionais: raíces 2, raíces 71, ... Os pitagóricos trataron de ocultar estes números (por non enfadarse aos deuses), pero logo apareceron como “inmensos”. Con todo, debido a fallos nos sistemas de numeración non se definiron correctamente. Os matemáticos europeos, aproveitando os avances, déronse conta de que eran números decimais inesgotables (nos que non se repetían cifras). Desta maneira conseguiron diferenciarse dos números racionais. Desde entón xurdiu o concepto de números algebraicos e de números transcendentes. Hoxe distínguese:

• Número irracional: que non é a solución de ningunha ecuación cun coeficiente global de primeira orde: , e, erro 7, erro 10, …
• Número algebraico: solución dun coeficiente completo e una ecuación algebraica: Solucións das ecuacións 2, erro 2, erro 7, ... x -2 = 0, x 2 - 2 = 0, x 3 - 7 = 0,...
• Número transcendente: coeficiente total ou fraccionado e non solución de ecuación: , e, log 2, cos 25º,...

Aínda que no novo sistema pódese escribir calquera número natural, os científicos adoptaron una escritura especial: 1000 = 10 3 ; 100.000 = 10 5 ; 82765900000000000 - 827659 x 10 11 ou utilizando a escritura de cómaa móbil 8,27659 x 10 16 .

Co novo sistema pódese plazar unha pregunta: cal é o número máis grande que se pode escribir? Esta pregunta deu lugar ao concepto de infinito. Hoxe representamos o infinito co símbolo. Foi utilizado por primeira vez en 1655 polo inglés John Wallis. Hai que diferenciar o concepto físico e matemático do infinito. O maior valor medido fisicamente foi 1042. É o número de protones e neutróns que hai no universo entre outras cousas.

Os matemáticos foron máis lonxe e inventaron números transfinitos. O primeiro deles é 0 (aleph-cero) (é a primeira letra do alfabeto hebraico). Isto representa o número de números naturais, impares, pares, racionais, etc.

Os dous descubrimentos que permitiron o avance da álxebra foron o novo sistema de cifras e a escritura simbólica lineal. A súa inventiva (1591) débese a François Viète. Viète xeneralizou a álxebra cando expresou números descoñecidos con x, e,... Este liberou a álxebra e o pensamento dos obxectos concretos e contribuíu a aproximarse ao razoamento abstracto.

En canto aos símbolos, na Idade Media o signo (-) denominouse minus e o signo (+) più. As palabras foron substituídas por ñ e p, ata que en 1489 o alemán Ricardo Widmann recoñeceu por primeira vez os símbolos coñecidos (+, -). En 1557 o inglés Robert Receke inventou o signo =, Thomas Harriot en 1631 en diferenzas e símbolos, William Oughtred en x (multiplicación) XVII. A principios do século XX e (raíz cadrada), símbolo (derivado da letra R), foi creado por Christoph Rudolf en 1525.

Aquí termina esta pequena historia das cifras, una pequena parte da historia xeral do ser humano.