Ander Zarketa Astigarraga

Texte rédigé en basque et traduit automatiquement par Elia sans révision postérieure. VOIR L'ORIGINAL

Qu'est-ce que c'est que l'entropie ?

Deux lois simples de la thermodynamique construisent la base de la discipline, mais l'entropie crée toujours le plus grand obstacle à la compréhension. Bien que le concept d'énergie soit colocalement saisissable, l'entropie a une charge sémantique confuse. Ce texte clarifie la signification technique des deux lois et fournit la clé pour comprendre l'entropie comme une propriété.

Ander Zarketa Astigarraga

Il y a quelques années que je suis en train de revenir avec une leçon basée sur la discipline de la thermodynamique. Je donne des cours sur un cours de master. Les étudiants sont donc des personnes qui ont obtenu le diplôme d'ingénieur. C'est-à-dire qu'au début du cours, lorsque nous passons en revue la leçon de degré équivalente au cours de master, les concepts développés en classe devraient leur être aussi intuitifs que compréhensibles. Il en est ainsi du moins jusqu'à ce que nous trébuchions sur la pierre éternelle. Une fois qu'on aura payé l'entropie, c'est fini. Chaos annuel : sourcils noirs, questions multiples, plus de doutes. Je finis par aborder l'habituel moyen pratique de sortir du port. C'est-à-dire, se concentrer sur les calculs et minimiser l'importance de la compréhension du concept.

Je suis conscient qu'en fait, je devrais mettre une grande partie de la charge sur les possibles insuffisances de mes capacités de communication. Cependant, je soupçonne que le reste du problème est lié à un autre facteur, à savoir la manière habituelle d'expliquer les bases de la thermodynamique.

Nous n'utilisons que deux lois dans toute la leçon. Ces lois ont un caractère empirique. En d'autres termes, au cours du XIXe siècle où ils ont été formulés, ils n'ont pas été déduits d'autres principes; ils ont été déduits directement des cas observés dans l'expérimentation quotidienne.

Jusqu'à présent, la Thermodynamique a connu de nombreux développements dans la discipline naissante qu'on appelait alors la Thermodynamique, et les notions propres qu'elle a enfantées se sont limitées à ce qu'on appelle la Thermodynamique classique. Ces autres développements ont donné naissance à de nouvelles disciplines: “Thermodynamique statistique”, “Thermodynamique quantique”, “Thermodynamique irréversible”, entre autres.

Comme on peut le déduire de ces dénominations, la complexité des phénomènes étudiés a augmenté, de même que la formulation des théories et des études. Or, ces augmentations de la multiplication des disciplines et de la complexité des phénomènes n'ont pas réussi à modifier le caractère fondamental de ces lois. On a jusqu'ici affirmé que, quel que soit le phénomène étudié, ou quelque théorie que ce soit, il faut obéir à ces deux lois. C'est l'importance de les comprendre et de les assimiler.

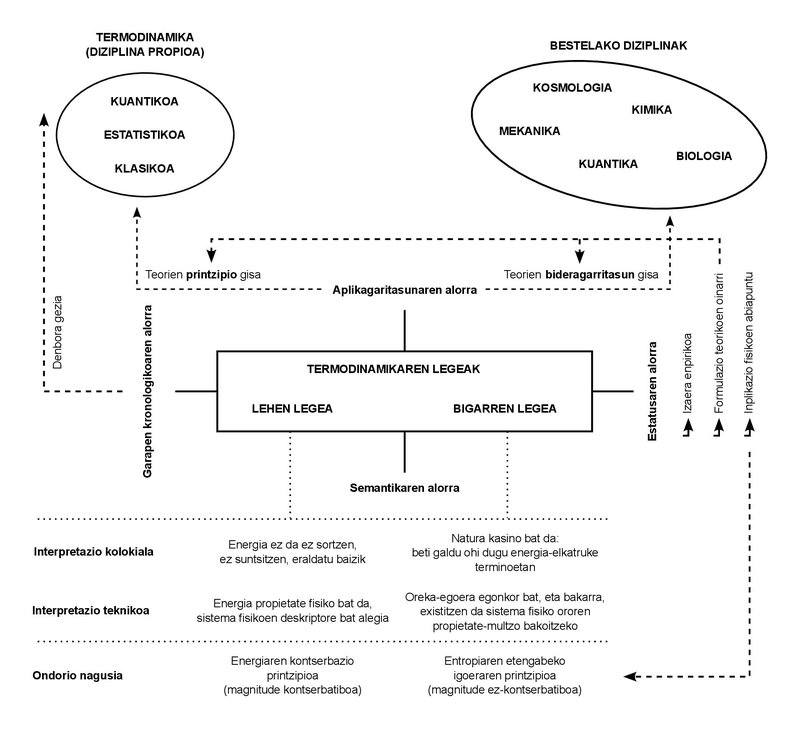
Que disent donc ces lois ? Si on les exprime simplement, elles sont très faciles à comprendre, et c'est avec cette simplicité que je les explique en classe. Première loi: l'énergie ne se crée pas, ne se détruit pas, mais se transforme. Ou en utilisant un terme un peu plus technique: l'énergie est conservée. Deuxième loi : La nature (ainsi en majuscules) est un casino, donc elle gagne toujours. En d’autres termes, nous pouvons interpréter notre échange avec la Nature comme un échange constant d’énergie et, dans le jeu que suppose ce sens, la Nature achève l’acquisition de toute pièce d’énergie. En troisième lieu, la quantité d'énergie qui peut nous être utile ou exploitable diminue constamment. Et la mesure la plus adéquate de cette diminution nous est apportée par une autre notion physique qui s'accroît parallèlement : les entropies.

La notion d'énergie nous est très intuitive. Nous l'employons au jour le jour, et nous nous servons de luy dans des situations qui ont diverses significations ou significations. C'est un concept à la fois polysémique et largement répandu. La loi de la conservation de l'énergie a un statut analogue : combien de fois aurions-nous jamais entendu parler de la location de la non-création, de la non-destruction, de la transformation ? De plus, la question de la conservation est également bien connue dans des disciplines autres que la thermodynamique : par exemple, la conservation de la quantité de mouvement et du moment angulaire en mécanique, ou la conservation de la masse dans des systèmes non relativistes.

les concepts de “conservation” et d’“énergie” nous sont donc totalement accessibles. Ils ont réussi à faire un parcours du langage technique au langage collégial. Ce n'est pas peu. La notion d'entropie, cependant, a rencontré plus d'obstacles pour cela. On ne peut pas dire qu'il n'est pas connu, bien qu'il soit en quelque sorte plus mystérieux que les deux autres. Cependant, ma mâchoire a la plus grande tension avec la signification commune et partagée de l'entropie. Comme pour mes élèves, je sais que tous ceux qui ont rencontré ce concept le associent à l'ignorance et au désordre.

Cette charge sémantique déroutante est tout à fait compréhensible. En fait, l'objectif de la thermodynamique classique est de décrire le comportement macroscopique des systèmes constitués de nombreuses particules. Combien de particules sont « abondantes », mais ? Au cas où, dans les systèmes typiques que nous étudions dans ma leçon de professeur, nous considérons les fluides de quelques litres et kilogrammes. Quelle que soit la substance que nous prenons comme fluide, le nombre de particules que nous pouvons trouver dans les systèmes de ces tailles est de l'ordre du nombre d'Avogadro, c'est-à-dire environ 10²³. En gros, le nombre d'Avogadro représente le nombre de particules dans une mole de n'importe quelle substance. On peut en quelque sorte assimiler le concept du mole à celui du kilogramme (c'est-à-dire quantifier la substance), mais c'est un peu plus basique en soi. En effet, un grand nombre de phénomènes mesurables du comportement physique de nombreuses substances est proportionnel au nombre de particules (et donc aux moules), et non pas à la masse. 10²³ particules, en revanche, sont suffisantes. L'ordre de la population mondiale approche les 10¹⁰. En un mot, même si nous possédions autant de planètes que d'habitants dans le monde, la population de toutes ces planètes (10²⁰) serait un peu éloignée d'atteindre le nombre de particules dans une mole. C'est un grand nombre. Que pouvons-nous dire sur le comportement macroscopique des systèmes de ces formes ? C'est essentiellement la question à laquelle répond la thermodynamique classique. Les concepts de «pression» ou de «température» que nous utilisons au quotidien font partie de la réponse à la question mentionnée.

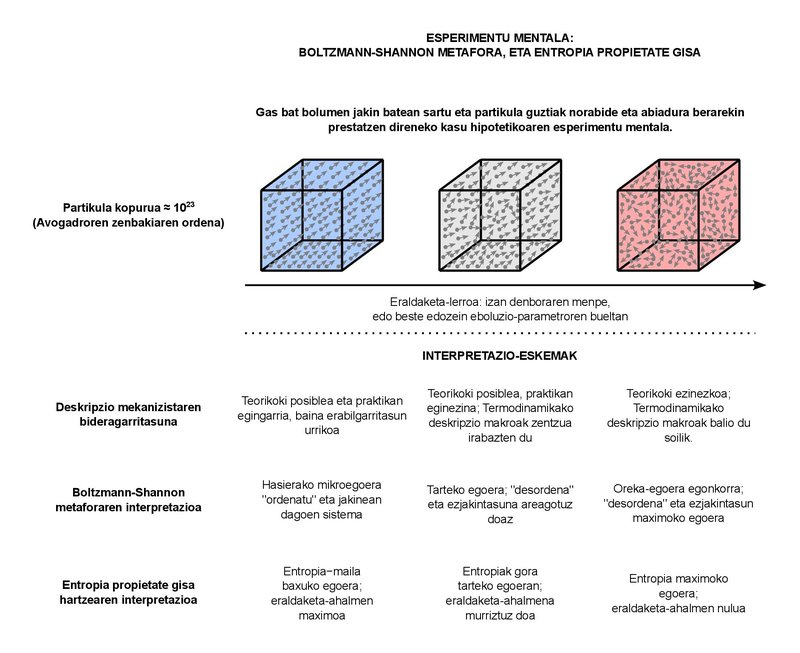
Il n'est pas surprenant, d'autre part, qu'il y ait un grand chaos dans les systèmes avec le nombre de particules de cet ordre. il est tout à fait impossible de suivre chacune de ces particules qui sont d'environ 10²³, de sorte que nous ne pouvons pas fournir une description mécanique complète du système. Au lieu de cela, nous utilisons les concepts de la thermodynamique statistique basés sur la physique statistique pour combiner de manière optimale les deux approches, la macro et la micro. Nous devrions placer la métaphore du désordre qui entoure l'entropie là. Dans le but de justifier cette augmentation constante de l'entropie qui est vérifiée dans le comportement macro-comportemental avec des concepts d'approche micro.

L'essence de la métaphore est due au physicien autrichien Ludwig Boltzmann, qui dit au fond que ces 10²³ particules peuvent être organisées de différentes manières. Nous pouvons donner à chaque forme d’organisation le nom de « micro-état ». Un système macroscopique, en principe, nous pouvons l'imaginer parfaitement défini. C'est-à-dire qu'il est dans l'un de tous les micro-états possibles. Lorsque le système subit une transformation, plusieurs micro-états compatibles avec l'approche macroscopique lui sont physiquement accessibles. Toutes ces micro-situations sont complémentaires, c'est-à-dire qu'elles sont physiquement possibles, d'une part, et inséparables du point de vue macroscopique, d'autre part. Comme l'augmentation des micro-états possibles suit la même tendance que l'augmentation continue de l'entropie, Boltzmann a basé sa définition de l'entropie sur la proportionnalité entre les deux. L'entropie serait donc l'inséparabilité macroscopique entre les formes de plus en plus nombreuses d'organisation des particules. C'est le désordre.

Des décennies plus tard, l'ingénieur Claude Shannon a ajouté le concept d'ignorance à la métaphore du désordre. Shannon était en train de théoriser les systèmes de communication et quand il a formulé mathématiquement la quantité d'informations contenues dans les messages, il a rencontré l'expression apparente de l'entropie couramment utilisée en thermodynamique. Il a ainsi associé l'augmentation de l'entropie dans un système à la perte d'informations sur ce système. Et avec la vision de Boltzmann s'est développé ainsi le sens commun que nous utilisons aujourd'hui : l'entropie, une grandeur qui exprime le degré d'ignorance et de désordre autour des systèmes physiques.

Après ce court parcours sémantique, seulement deux points. Premièrement, les significations colocales des concepts exprimés (énergie, conservation, entropie) doivent être utilisées avec prudence. Bien qu'ils puissent refléter correctement l'idée clé de leurs équivalents techniques, ils peuvent laisser des nuances importantes à l'extérieur. Et deuxièmement : Il en est de même des expressions vulgaires des deux lois de la thermodynamique, c'est-à-dire qu'elles brouillent en quelque sorte la charge technique qu'elles supportent. En fait, la conservation de l'énergie n'est pas une formulation de la première loi, mais l'une des conséquences. En réalité, le sens abstrait de la première loi dit que l'énergie peut être définie comme une propriété physique. Ce serait sa signification la plus profonde.

Il en est de même pour la seconde loi. L'image du casino peut être didactique d'une certaine manière, mais il n'est pas entièrement technique. En l'énonçant formellement, la deuxième loi codifie seulement l'existence d'états d'équilibre stables. C'est un fait empirique que tout système tend à l'équilibre. Or, de tous les états d'équilibre, la deuxième loi dit qu'il n'y a qu'un seul état d'équilibre stable pour chaque valeur prise par l'ensemble de grandeurs qui décrit le système. La conséquence directe de la combinaison des deux lois est donc que l'entropie magnitude, en tant qu'énergie, est une propriété, car c'est la propriété qui indique qu'un système a atteint son état d'équilibre stable, car l'entropie présente la valeur maximale qu'il peut atteindre dans cet état.

L'énergie et l'entropie ne sont donc pas si différentes. Les deux sont des propriétés physiques, c'est-à-dire des magnitudes qui peuvent être utilisées pour décrire l'état physique de tout système. Les plus basiques, en effet, sont ceux qui découlent le plus directement des deux lois. Et en tant que propriétés, ils sont définis de manière appropriée pour tous les états du système, qu'il s'agisse d'états d'équilibre ou hors équilibre, stables ou non. De plus, comme pour le concept d'énergie, l'entropie n'est pas une grandeur statistique ou informationnelle, même si elle prend ses propres expressions dans ces domaines.

En tant que propriété, l'énergie quantifie les potentialités d'échange d'un système, tandis que l'entropie se concentre sur la capacité de transformation. Plus l'entropie est élevée, plus la capacité de transformation est faible. Lorsque l'état d'équilibre est stable, l'entropie atteint sa valeur maximale et la puissance de transformation est nulle. Plus que le désordre maximum et l'ignorance totale, nous aurons l'ordre parfait et toute la connaissance du système: en effet, il ne pourra pas être dans un autre état d'équilibre stable que celui-ci.