¿Qué es eso de la entropía?
Las dos leyes simples de la termodinámica construyen la base de la disciplina, pero la entropía siempre crea el mayor obstáculo de comprensión. Aunque el concepto de energía es coloquialmente accesible, la entropía tiene una carga semántica confusa. Este texto aclara el significado técnico de ambas leyes y ofrece la clave para entender la entropía como propiedad.

Hace ya unos años que vuelvo con una asignatura que tiene como base la disciplina de la Termodinámica. Doy clases en un curso de máster. Los alumnos son, por tanto, personas que han obtenido el título de ingeniero. Es decir, al inicio del curso, cuando hacemos un repaso de la asignatura de grado que equivale al curso de máster, los conceptos expuestos en clase deberían hacerse tan comprensiblemente intuitivos. Al menos así es hasta que tropezamos con la piedra de siempre. Al llegar a la cuenta de la entropía, se acabó. Anabasa anual: ceños oscuros, muchas preguntas, más dudas. Al final, me agarro a la forma práctica de siempre salir de la compuerta. Es decir, prestar atención a los cálculos y restar importancia a la comprensión del concepto.
Soy consciente de que en realidad debería poner gran parte de la carga en las posibles deficiencias de mis capacidades de comunicación. Sospecho, sin embargo, que el resto del problema tiene que ver con otro factor, la forma habitual en que se explican los fundamentos de la Termodinámica.
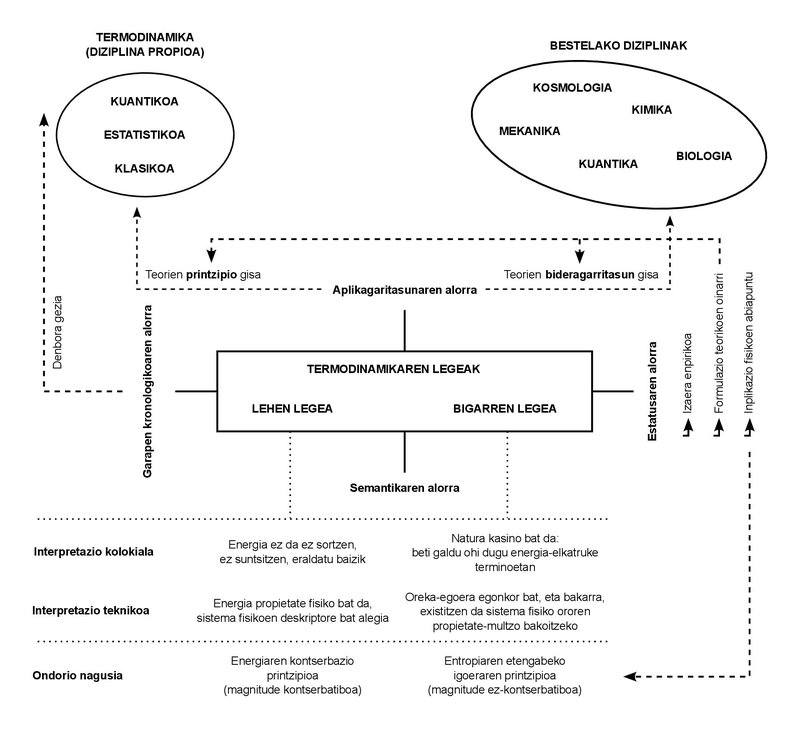
Solo usamos dos leyes en toda la lección. Estas leyes tienen un carácter empírico. En otras palabras: en aquel siglo XIX de su formulación, no se dedujeron de otros principios, sino que fueron deducidos directamente de los casos observados en la experimentación cotidiana.
Hoy, por otro lado, son muchos los desarrollos que ha sufrido la incipiente disciplina que en aquella ocasión se denominó Termodinámica, y los conceptos propios que dio a luz han quedado limitados al campo de la denominada “Termodinámica Clásica”. Estos otros desarrollos han dado a luz nuevas disciplinas: “Termodinámica estadística”, “Termodinámica cuántica”, “Termodinámica irreversible”, entre otras.
Tal y como se desprende de estas designaciones, ha aumentado la complejidad de los fenómenos estudiados, así como la formulación de teorías e investigaciones. Sin embargo, la proliferación de disciplinas y el incremento de la complejidad de los fenómenos no han logrado alterar el carácter básico de las leyes citadas. Cualquiera que sea el fenómeno estudiado, o sea la teoría formulada, se ha confirmado que ambas leyes deben cumplir lo que se les impuso. Es la importancia de comprenderlos y de interiorizarlos.
¿Qué dicen esas leyes? Si las hablo con palabras sencillas son muy fáciles de comprender, y aprovecho para explicarlas también en clase. Primera ley: la energía no se crea ni se destruye, sino que se transforma. O usando un término más técnico de alguna manera: la energía se conserva. Segunda ley: La naturaleza (en mayúsculas) es un casino, por lo que siempre gana. En otras palabras, podemos interpretar nuestro intercambio con la Naturaleza como un continuo intercambio de energía, y en el juego que supone este sentido, la Naturaleza termina por adquirir toda moneda de energía. Incluso de una tercera manera: la cantidad de energía que nos puede ser útil o explotable va disminuyendo constantemente. Y el mejor medidor de esta disminución es otro concepto físico que aumenta de forma paralela: la entropía.
El concepto de energía es muy intuitivo. Lo usamos en el día a día, y lo usamos en situaciones que tienen diferentes significados o significados. Es un concepto polisémico tan extendido. La ley de conservación de la energía tiene un estatus similar: ¿cuántas veces habríamos oído esta alocución de no generación, no destrucción, sino de transformación? Es más, el tema de la conservación es muy conocido en otras disciplinas diferentes a la Termodinámica: por ejemplo, la conservación de la cantidad de movimiento y del momento angular en la Mecánica, o la conservación de la masa en sistemas no relativistas.
los conceptos de “conservación” y “energía”, por lo tanto, nos son totalmente accesibles. Han conseguido hacer un recorrido desde el lenguaje técnico hasta el coloquial. No es poco. Sin embargo, la noción de entropía ha tenido más obstáculos para ello. No se puede decir que no sea conocido, aunque sea de alguna manera más misterioso que los otros dos mencionados. Sin embargo, mi matraca tiene la mayor tensión precisamente con el significado común y compartido de la entropía. Como me ocurre con los alumnos, soy consciente de que todo aquel que se ha encontrado con este concepto lo relaciona también con la ignorancia y el desorden.
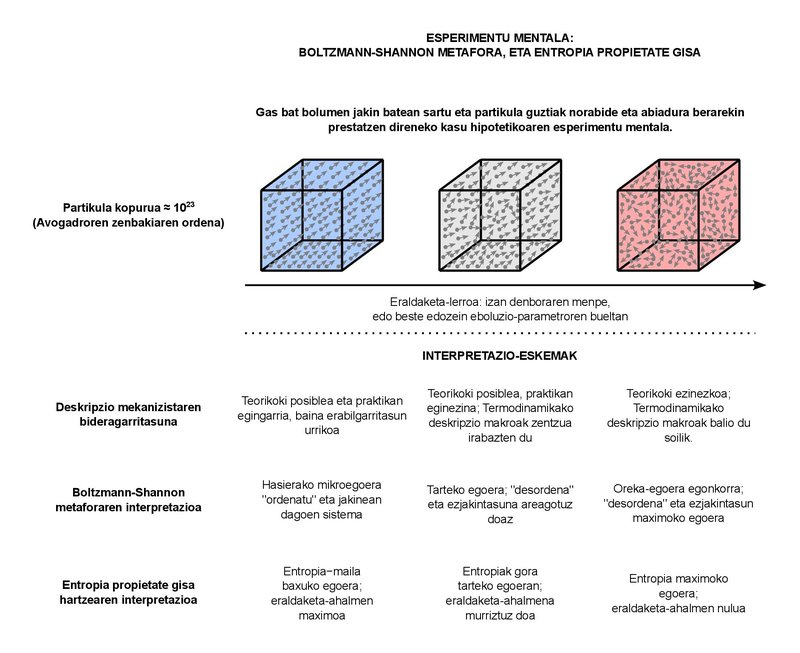
Esta perturbadora carga semántica es muy comprensible. De hecho, el objetivo de la Termodinámica clásica es describir el comportamiento macroscópico de los sistemas formados por numerosas partículas. ¿Cuántas partículas son “abundantes” pero? Por ejemplo, en la lección en la que soy profesor, echemos en cuenta que en los sistemas típicos que estudiamos tomamos fluidos de muy pocos litros y kilogramos. Sea cual sea la sustancia que tomemos como fluido, el número de partículas que podemos encontrar en los sistemas de estos tamaños es del orden del número de Avogadro, es decir, unos 10 23. Básicamente, el número de Avogadro representa el número de partículas que hay en un mol de cualquier sustancia. Podemos equiparar el concepto de mol al de kilogramo (que es el que cuantifica la sustancia), pero es algo más básico en sí mismo. De hecho, numerosos fenómenos mensurables de comportamiento físico de muchas sustancias son proporcionales al número de partículas (y por tanto a los moles), no tanto a la masa. 10 23 partículas son suficientes. Tenga en cuenta que el orden de la población mundial se está acercando a alrededor de 10 10. En términos sencillos, si bien tendríamos tantos planetas como habitantes hay en el mundo, la población (10 20) almacenada en todos ellos estaría un poco alejada de llegar al número de partículas que aún se encuentran en un mol. Por lo menos un número enorme. ¿Qué podemos decir del comportamiento macroscópico de estos sistemas? Esta es básicamente la pregunta a la que responde la Termodinámica clásica. Los conceptos de “presión” o “temperatura” que manejamos en el día a día forman parte de la respuesta dada a la pregunta.
No es de extrañar, por otra parte, que los sistemas con número de partículas de este orden presenten un gran caos. cada una de estas partículas, que son aproximadamente 10 23, es completamente imposible de seguir, por lo que no podemos proporcionar una descripción mecanicista completa del sistema. En su lugar, utilizamos los conceptos de Termodinámica estadística basados en la Física estadística para combinar de forma adecuada los dos enfoques, la macro y la micro. Deberíamos ubicar ahí la metáfora del desorden en torno a la entropía. En un esfuerzo por justificar con conceptos de visión micro este aumento constante de entropía que se verifica en el comportamiento macro.
El fundamento de la metáfora se lo debemos al físico austriaco Ludwig Boltzmann, que en el núcleo dice que, en realidad, estas 10 23 partículas pueden estar organizadas de muchas maneras. Podemos denominar a cada modo de organización como “microestado”. Un sistema macroscópico se puede representar, en principio, completamente definido. Es decir, está en una de todas las microsituaciones posibles. Cuando el sistema sufre una transformación, se le hacen físicamente accesibles múltiples microestados compatibles con el enfoque macroscópico. Todos estos microestados son complementarios, es decir, físicamente posibles, por un lado, e inseparables desde el punto de vista macroscópico, por otro. Dado que el aumento de los posibles microestados es igual a la tendencia constante de aumento de la entropía, Boltzmann formuló su definición de entropía basándose en la proporcionalidad entre ambos. Así, la entropía sería la indisolubilidad macroscópica entre los modos cada vez más numerosos de organización de las partículas. Ese es el desorden.
Décadas más tarde, el ingeniero Claude Shannon añadió el concepto de la ignorancia a la metáfora del desorden. Shannon está llevando a cabo una teorización de los sistemas de comunicación y, al formular matemáticamente la cantidad de información que contienen los mensajes, se encuentra con la expresión aparente de la entropía, utilizada en la Termodinámica. Relacionó el aumento de entropía en un sistema con la pérdida de información sobre el mismo. Y, junto con la visión de Boltzmann, se desarrolló así la acepción común con la que nos encontramos en la actualidad: la entropía, magnitud que expresa el grado de ignorancia y desorden en torno a los sistemas físicos.
Tras este breve recorrido semántico, solo dos puntos. Primero: los significados coloquiales (energía, conservación, entropía) de los conceptos expresados deben utilizarse con cautela. Aunque pueden reflejar adecuadamente la idea clave de sus equivalentes técnicos, pueden dejar fuera importantes matices. Y la segunda: Lo mismo ocurre con las expresiones usuales de las dos leyes de la termodinámica, que empañan de algún modo la carga técnica que soportan. De hecho, la conservación de la energía no es una formulación de la primera ley, sino una de sus consecuencias. De hecho, el sentido abstracto de la primera ley es que la energía puede ser definida como propiedad física. Ese sería su significado más profundo.
Con la segunda ley pasa de la misma manera. La imagen del casino puede ser de alguna manera didáctica, pero no es del todo técnica. Al expresarlo formalmente, la segunda ley solo codifica la existencia de estados estables de equilibrio. El hecho empírico de que todo sistema tiende al equilibrio. Pues bien, entre todos los estados de equilibrio, la segunda ley dice que para cada valor que toma el conjunto de magnitudes que describe el sistema hay un único estado de equilibrio estable. La consecuencia directa de la combinación de ambas leyes es que la magnitud entropía, como energía, es una propiedad que indica que un sistema ha llegado a su estado estable de equilibrio, en el que la entropía refleja el valor máximo que puede adquirir.
La energía y la entropía, por tanto, no son tan diferentes. Ambas son propiedades físicas, es decir, magnitudes que se pueden utilizar para describir el estado físico de cualquier sistema. Las más elementales, por cierto, porque se derivan de la manera más directa de ambas leyes. Y, como propiedades, están definidas de manera adecuada para todos los estados del sistema, ya sean estados de equilibrio o fuera de equilibrio, estables o no. Es más, y al igual que ocurre con el concepto de energía, la entropía no es una magnitud estadística o informacional, aunque en estos campos asuma sus propias manifestaciones.
Como propiedad, la energía cuantifica las capacidades de intercambio que tiene un sistema, mientras que la entropía se centra en la capacidad de transformación. A mayor entropía, menor poder de transformación. Al llegar al estado de equilibrio estable, la entropía tomará el valor máximo y la capacidad de transformación será nula. Más que un desorden máximo y un desconocimiento total, tendremos un orden perfecto y todo el conocimiento del sistema: de hecho, no podrá estar en un estado de equilibrio diferente al que se está.
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian











