Què és això de l'entropia?
Les dues lleis simples de la termodinàmica construeixen la base de la disciplina, però l'entropia sempre crea el major obstacle de comprensió. Encara que el concepte d'energia és col·loquialment accessible, l'entropia té una càrrega semàntica confusa. Aquest text aclareix el significat tècnic de totes dues lleis i ofereix la clau per a entendre l'entropia com a propietat.

Fa ja uns anys que torno amb una assignatura que té com a base la disciplina de la Termodinàmica. Faig classes en un curs de màster. Els alumnes són, per tant, persones que han obtingut el títol d'enginyer. És a dir, a l'inici del curs, quan fem un repàs de l'assignatura de grau que equival al curs de màster, els conceptes exposats en classe haurien de fer-se tan comprensiblement intuïtius. Almenys així és fins que ensopeguem amb la pedra de sempre. En arribar al compte de l'entropia, es va acabar. Anabasa anual: ceños foscos, moltes preguntes, més dubtes. Al final, m'agarro a la forma pràctica de sempre sortir de la comporta. És a dir, parar esment als càlculs i restar importància a la comprensió del concepte.
Soc conscient que en realitat hauria de posar gran part de la càrrega en les possibles deficiències de les meves capacitats de comunicació. Sospito, no obstant això, que la resta del problema té a veure amb un altre factor, la forma habitual en què s'expliquen els fonaments de la Termodinàmica.
Només usem dues lleis en tota la lliçó. Aquestes lleis tenen un caràcter empíric. En altres paraules: en aquell segle XIX de la seva formulació, no es van deduir d'altres principis, sinó que van ser deduïts directament dels casos observats en l'experimentació quotidiana.
Avui, d'altra banda, són molts els desenvolupaments que ha sofert la incipient disciplina que en aquella ocasió es va denominar Termodinàmica, i els conceptes propis que va donar a llum han quedat limitats al camp de la denominada “Termodinàmica Clàssica”. Aquests altres desenvolupaments han donat a llum noves disciplines: “Termodinàmica estadística”, “Termodinàmica quàntica”, “Termodinàmica irreversible”, entre altres.
Tal com es desprèn d'aquestes designacions, ha augmentat la complexitat dels fenòmens estudiats, així com la formulació de teories i recerques. No obstant això, la proliferació de disciplines i l'increment de la complexitat dels fenòmens no han aconseguit alterar el caràcter bàsic de les lleis citades. Qualsevol que sigui el fenomen estudiat, o sigui la teoria formulada, s'ha confirmat que totes dues lleis han de complir el que se'ls va imposar. És la importància de comprendre'ls i d'interioritzar-los.
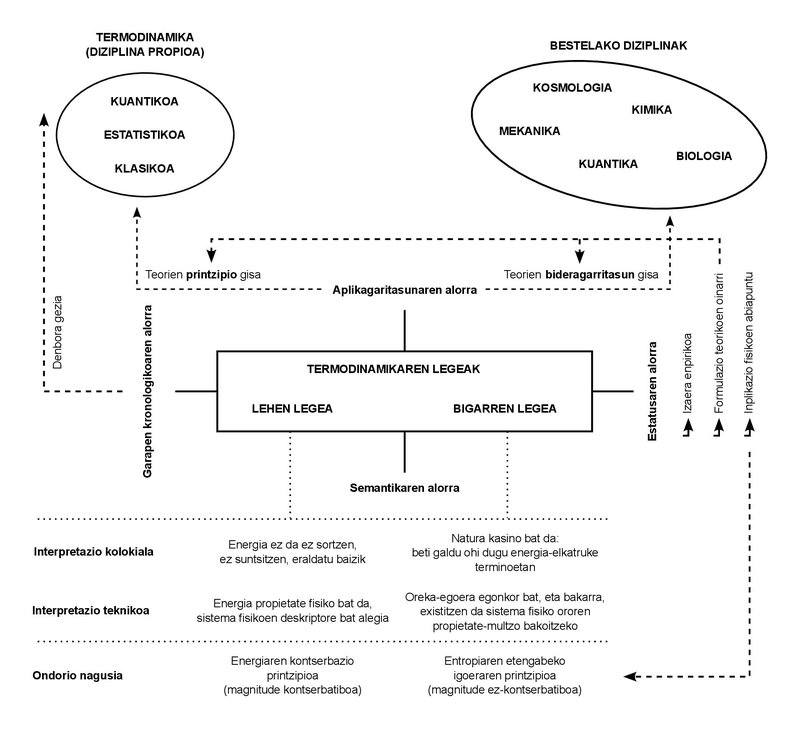
Què diuen aquestes lleis? Si les parlo amb paraules senzilles són molt fàcils de comprendre, i aprofito per a explicar-les també en classe. Primera llei: l'energia no es crea ni es destrueix, sinó que es transforma. O usant un terme més tècnic d'alguna manera: l'energia es conserva. Segona llei: La naturalesa (en majúscules) és un casino, per la qual cosa sempre gana. En altres paraules, podem interpretar el nostre intercanvi amb la Naturalesa com un continu intercanvi d'energia, i en el joc que suposa aquest sentit, la Naturalesa acaba per adquirir tota moneda d'energia. Fins i tot d'una tercera manera: la quantitat d'energia que ens pot ser útil o explotable va disminuint constantment. I el millor mesurador d'aquesta disminució és un altre concepte físic que augmenta de manera paral·lela: l'entropia.
El concepte d'energia és molt intuïtiu. Ho usem en el dia a dia, i l'usem en situacions que tenen diferents significats o significats. És un concepte polisèmic tan estès. La llei de conservació de l'energia té un estatus similar: quantes vegades hauríem sentit aquesta al·locució de no generació, no destrucció, sinó de transformació? És més, el tema de la conservació és molt conegut en altres disciplines diferents a la Termodinàmica: per exemple, la conservació de la quantitat de moviment i del moment angular en la Mecànica, o la conservació de la massa en sistemes no relativistes.
els conceptes de “conservació” i “energia”, per tant, ens són totalment accessibles. Han aconseguit fer un recorregut des del llenguatge tècnic fins al col·loquial. No és poc. Tanmateix, la noció d'entropia ha tingut més obstacles per a això. No es pot dir que no sigui conegut, encara que sigui d'alguna manera més misteriós que els altres dos esmentats. No obstant això, la meva matraca té la major tensió precisament amb el significat comú i compartit de l'entropia. Com m'ocorre amb els alumnes, soc conscient que tot aquell que s'ha trobat amb aquest concepte el relaciona també amb la ignorància i el desordre.
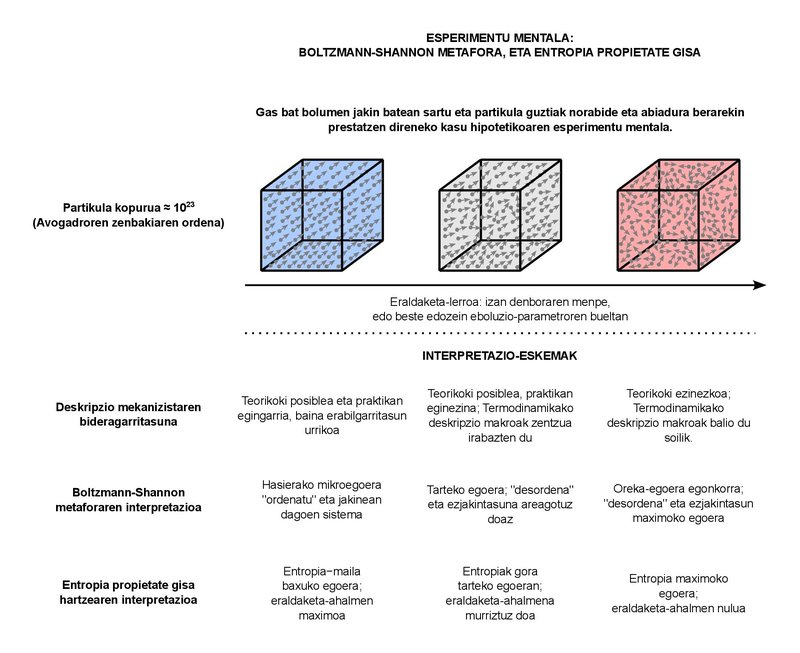
Aquesta pertorbadora càrrega semàntica és molt comprensible. De fet, l'objectiu de la Termodinàmica clàssica és descriure el comportament macroscòpic dels sistemes formats per nombroses partícules. Quantes partícules són “abundants” però? Per exemple, en la lliçó en la qual soc professor, tirem en compte que en els sistemes típics que estudiem prenem fluids de molt pocs litres i quilograms. Sigui com sigui la substància que prenguem com a fluid, el nombre de partícules que podem trobar en els sistemes d'aquestes grandàries és de l'ordre del número d'Avogadro, és a dir, uns 10 23. Bàsicament, el número d'Avogadro representa el nombre de partícules que hi ha en un mol de qualsevol substància. Podem equiparar el concepte de mol al de quilogram (que és el que quantifica la substància), però és una mica més bàsic en si mateix. De fet, nombrosos fenòmens mesurables de comportament físic de moltes substàncies són proporcionals al nombre de partícules (i per tant als mols), no tant a la massa. 10 23 partícules són suficients. Tingui en compte que l'ordre de la població mundial s'està acostant a al voltant de 10 10. En termes senzills, si bé tindríem tants planetes com habitants hi ha en el món, la població (10 20) emmagatzemada en tots ells estaria una mica allunyada d'arribar al nombre de partícules que encara es troben en un mol. Almenys un número enorme. Què podem dir del comportament macroscòpic d'aquests sistemes? Aquesta és bàsicament la pregunta a la qual respon la Termodinàmica clàssica. Els conceptes de “pressió” o “temperatura” que manegem en el dia a dia formen part de la resposta donada a la pregunta.
No és d'estranyar, d'altra banda, que els sistemes amb nombre de partícules d'aquest ordre presentin un gran caos. cadascuna d'aquestes partícules, que són aproximadament 10 23, és completament impossible de seguir, per la qual cosa no podem proporcionar una descripció mecanicista completa del sistema. En el seu lloc, utilitzem els conceptes de Termodinàmica estadística basats en la Física estadística per a combinar de forma adequada els dos enfocaments, la macro i la micro. Hauríem de situar aquí la metàfora del desordre entorn de l'entropia. En un esforç per justificar amb conceptes de visió micro aquest augment constant d'entropia que es verifica en el comportament macro.
El fonament de la metàfora li ho devem al físic austríac Ludwig Boltzmann, que en el nucli diu que, en realitat, aquestes 10 23 partícules poden estar organitzades de moltes maneres. Podem denominar a cada mode d'organització com a “microestat”. Un sistema macroscòpic es pot representar, en principi, completament definit. És a dir, està en una de totes les microsituacions possibles. Quan el sistema sofreix una transformació, se li fan físicament accessibles múltiples microestats compatibles amb l'enfocament macroscòpic. Tots aquests microestats són complementaris, és a dir, físicament possibles, d'una banda, i inseparables des del punt de vista macroscòpic, per un altre. Atès que l'augment dels possibles microestats és igual a la tendència constant d'augment de l'entropia, Boltzmann va formular la seva definició d'entropia basant-se en la proporcionalitat entre tots dos. Així, l'entropia seria la indissolubilitat macroscòpica entre els modes cada vegada més nombrosos d'organització de les partícules. Aquest és el desordre.
Dècades més tard, l'enginyer Claude Shannon va afegir el concepte de la ignorància a la metàfora del desordre. Shannon està duent a terme una teorització dels sistemes de comunicació i, en formular matemàticament la quantitat d'informació que contenen els missatges, es troba amb l'expressió aparent de l'entropia, utilitzada en la Termodinàmica. Va relacionar l'augment d'entropia en un sistema amb la pèrdua d'informació sobre aquest. I, juntament amb la visió de Boltzmann, es va desenvolupar així l'accepció comuna amb la qual ens trobem en l'actualitat: l'entropia, magnitud que expressa el grau d'ignorància i desordre entorn dels sistemes físics.
Després d'aquest breu recorregut semàntic, només dos punts. Primer: els significats col·loquials (energia, conservació, entropia) dels conceptes expressats han d'utilitzar-se amb cautela. Encara que poden reflectir adequadament la idea clau dels seus equivalents tècnics, poden deixar fos importants matisos. I la segona: El mateix ocorre amb les expressions usuals de les dues lleis de la termodinàmica, que entelen d'algun mode la càrrega tècnica que suporten. De fet, la conservació de l'energia no és una formulació de la primera llei, sinó una de les seves conseqüències. De fet, el sentit abstracte de la primera llei és que l'energia pot ser definida com a propietat física. Aquest seria el seu significat més profund.
Amb la segona llei passa de la mateixa manera. La imatge del casino pot ser d'alguna manera didàctica, però no és del tot tècnica. En expressar-ho formalment, la segona llei només codifica l'existència d'estats estables d'equilibri. El fet empíric que tot sistema tendeix a l'equilibri. Doncs bé, entre tots els estats d'equilibri, la segona llei diu que per a cada valor que pren el conjunt de magnituds que descriu el sistema hi ha un únic estat d'equilibri estable. La conseqüència directa de la combinació de totes dues lleis és que la magnitud entropia, com a energia, és una propietat que indica que un sistema ha arribat al seu estat estable d'equilibri, en el qual l'entropia reflecteix el valor màxim que pot adquirir.
L'energia i l'entropia, per tant, no són tan diferents. Ambdues són propietats físiques, és a dir, magnituds que es poden utilitzar per a descriure l'estat físic de qualsevol sistema. Les més elementals, per cert, perquè es deriven de la manera més directa de totes dues lleis. I, com a propietats, estan definides de manera adequada per a tots els estats del sistema, ja siguin estats d'equilibri o fora d'equilibri, estables o no. És més, i igual que ocorre amb el concepte d'energia, l'entropia no és una magnitud estadística o informacional, encara que en aquests camps assumeixi les seves pròpies manifestacions.
Com a propietat, l'energia quantifica les capacitats d'intercanvi que té un sistema, mentre que l'entropia se centra en la capacitat de transformació. A major entropia, menor poder de transformació. En arribar a l'estat d'equilibri estable, l'entropia prendrà el valor màxim i la capacitat de transformació serà nul·la. Més que un desordre màxim i un desconeixement total, tindrem un ordre perfecte i tot el coneixement del sistema: de fet, no podrà estar en un estat d'equilibri diferent del qual s'està.
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian











