Zer da, baina, entropia delako hori?

Badira urte batzuk Termodinamikaren diziplina oinarri duen ikasgai batekin bueltaka nabilela. Masterreko kurtso batean ematen ditut klaseak. Ikasleak, beraz, ingeniari-titulua eskuratu duten pertsonak dira. Hau da, ikasturtearen hasieran, masterreko kurtsoak baliokide duen graduko ikasgaiaren errepasoa egiten dugunean, ulerterraz bezain intuitibo egin beharko litzaizkieke klasean azalduriko kontzeptuak. Hala izan ohi da, bederen, harik eta betiko harriarekin estropezu egiten dugun arte. Entropiaren kontura iristean, akabo. Urteroko anabasa: bekozko ilunak, galdera anitz, zalantza gehiago. Azkenean, atakatik irtetzeko betiko modu praktikoari heltzen diot. Alegia, arreta kalkuluetan jarri, eta kontzeptuaren ulermenari garrantzia kendu.

Jakitun naiz, berez, nire komunikazio-ahalmenen urritasun posibleetan jarri beharko nukeela zamaren zati handi bat. Susmoa daukat, ordea, arazoaren gainontzekoak bestelako faktore batekin duela zerikusia, hau da, Termodinamikako oinarriak azaltzen diren ohiko moduarekin.

Bi lege baino ez ditugu baliatzen ikasgai guztian. Legeok izaera enpirikoa dute. Bestela esanda: formulatu zireneko XIX. mende hartan, ez ziren ondorioztatu bestelako printzipio batzuetatik; eguneroko esperimentazioan behatutako kasuetatik deduzitu ziren, modu zuzenean.

Gaurdainokoan, bestalde, garapen ugari jasan ditu orduko hartan Termodinamika gisa izendaturiko diziplina hasiberriak, eta berorrek erditu zituen kontzeptu propioak “Termodinamika klasikoa” izeneko alorrera mugaturik geratu dira. Bestelako garapen horiek diziplina berriak erditu dituzte: “Termodinamika estatistikoa”, “Termodinamika kuantikoa”, “Termodinamika itzulezina”, beste batzuen artean.

Izendapen horietatik ondoriozta daitekeen moduan, azterturiko fenomenoen konplexutasunak gora egin du, baita teoria eta ikerketen formulazioak ere. Alabaina, diziplinen ugaritze- eta fenomenoen konplexutasun-igoera horiek ez dute lortu aipaturiko legeen oinarrizko izaera aldaraztea. Edozein dela-eta azterturiko fenomenoa, edo nolanahikoa izan formulaturiko teoria, bi legeok inposaturikoa bete behar dutela baieztatu da orain artekoan. Horratx berauek ulertu eta barneratzearen garrantzia.

Zer diote, bada, lege horiek? Hitz xumez adieraziz gero ulerterrazak dira oso, eta xumetasun horretaz baliatuz azaldu ohi ditut klasean ere. Lehen legea: energia ez da ez sortzen, ez eta suntsitzen, eraldatu baizik. Edo nolabait teknikoagoa den termino bat erabiliz: energia kontserbatu egiten da. Bigarren legea: Natura (halaxe, hizki larriz) kasino bat da, eta, beraz, beti irabazi ohi du. Bestela esanda, Naturarekin dugun hartu-emana etengabeko energia-elkartruke moduan interpreta dezakegu, eta, adiera horrek suposatzen duen jolasean, Naturak amaitzen du energia-txanpon oro eskuratzen. Are hirugarren modu batean: erabilgarria edo ustiagarria izan dakiguken energia-kantitatea gutxituz doa etengabe. Eta urritze horren neurgailurik aproposena modu paraleloan handitzen den beste kontzeptu fisiko batek dakarkigu: entropiak, alegia.

Energiaren kontzeptua intuitiboa zaigu oso. Egunerokotasunean darabilgu, eta esanahi edo adiera desberdinak dituzten egoeretan baliatzen gara hartaz. Kontzeptu polisemiko bezain zabaldua da. Energiaren kontserbazio-legeak ere pareko estatusa dauka: zenbatetan entzungo genuen ez-sortze, ez-suntsitze baizik eta eraldatzearen alokuzio hori? Are gehiago, kontserbazioaren kontua Termodinamikaz bestelako diziplinetan ere arras ezaguna da: adibidez, higidura-kantitatearen eta momentu angeluarraren kontserbazioa Mekanikan, edo masaren kontserbazioa sistema ez-erlatibistetan.

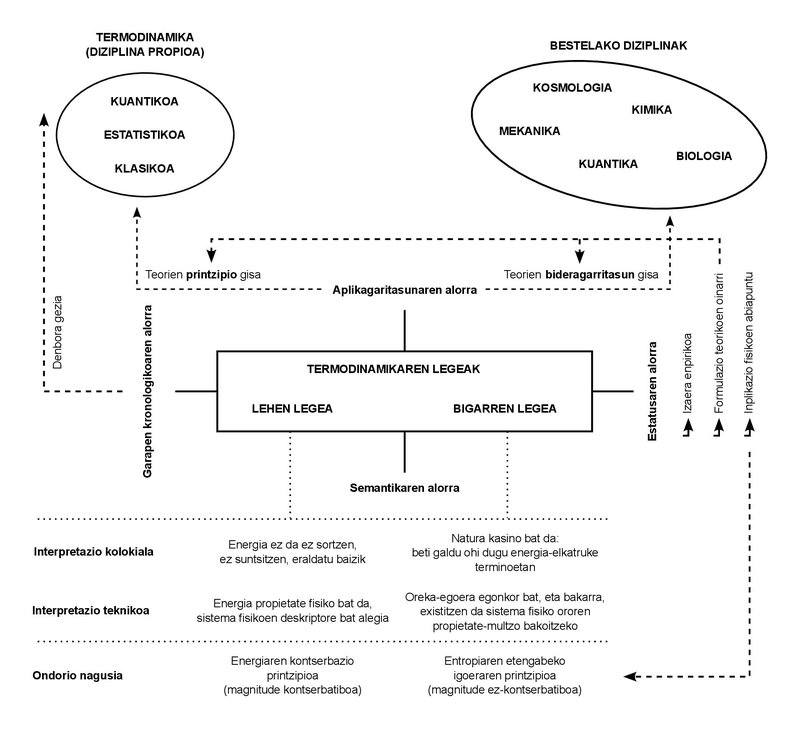
“Kontserbazio” eta “energia” kontzeptuak, beraz, atzigarriak zaizkigu erabat. Hizkera teknikotik kolokialerainoko ibilbidea egitea lortu dute. Ez da gutxi. Entropiaren nozioak, ordea, oztopo gehiago izan ditu horretarako. Ezin esan ez denik ezaguna, nahiz eta aipaturiko beste biak baino misteriotsuagoa izan nolabait. Hala ere, nire matrakak entropiaren esanahi arrunt eta konpartituarekin du, hain justu, tirabira handiena. Ikasleekin gertatzen zaidan moduan, jakitun naiz kontzeptu honekin topo egin duen orok ere ezjakintasun eta desordenarekin lotzen duela.

Karga semantiko nahasgarri hori ulergarria da oso. Izatez, Termodinamika klasikoaren helburua partikula ugariz eratutako sistemen portaera makroskopikoa deskribatzea da. Zenbat partikula dira “ugari”, baina? Kasurako, bota irakasle naizeneko ikasgaian aztertzen ditugun sistema tipikoetan litro eta kilogramo gutxiko fluidoak hartzen ditugula aintzat. Fluido gisa edozein sustantzia hartzen dugula ere, tamaina horietako sistemetan aurkitu dezakegun partikula-kopurua Avogadroren zenbakiaren ordenakoa da, hots, 10²³ inguru. Funtsean, Avogadroren zenbakiak edozein sustantziaren mol batean dagoen partikula-kopurua adierazten du. Molaren kontzeptua kilogramoarenarekin parekatu dezakegu nolabait (sustantzia kuantifikatzen du, alegia), baina zertxobait oinarrizkoagoa da, berez. Izan ere, sustantzia askoren portaera fisikoko fenomeno neurgarri ugari proportzionala da partikula-kopuruarekiko (eta, beraz, molekiko), ez horrenbeste masarekiko. 10²³ partikula, bestalde, nahikotxo dira. Kontu izan munduko biztanleriaren ordena 10¹⁰ ingurura gerturatzen ari dela. Hitz xumez: munduan dagoen biztanle adina planeta berdin izango bagenituzke ere, horietan guztietan bildutako biztanleria (10²⁰) urrun xamar egongo litzateke oraindik mol batean dagoen partikula-kopurura heltzetik. Zenbaki itzela, bederen. Zer esan dezakegu tankera horietako sistemen portaera makroskopikoaren inguruan? Horixe da, funtsean, Termodinamika klasikoak erantzuten duen galdera. Egunerokotasunean darabiltzagun “presio” edo “tenperatura” kontzeptuak aipaturiko galderari emandako erantzunaren parte dira.

Ez da harritzekoa, bestalde, ordena horretako partikula-kopurua duten sistemetan anabasa handia egotea. 10²³ inguru diren partikula horietako bakoitzari jarraitzea ezinezkoa da erabat, eta, beraz, ezin dezakegu sistemaren deskribapen mekanizista osatu bat eman. Horren ordez, Fisika estatistikoan oinarritutako Termodinamika estatistikoko kontzeptuak darabiltzagu bi ikuspegiak, makroa eta mikroa, modu aproposean uztartzeko. Entropiaren inguruko desordenaren metafora hor kokatu beharko genuke. Portaera makroan egiaztatzen den entropiaren etengabeko igoera hori ikuspegi mikroko kontzeptuekin justifikatzeko ahaleginean, alegia.

Metaforaren funtsa Ludwig Boltzmann fisikari austriarrari zor diogu, eta, muinean, hala dio: berez, 10²³ partikula horiek modu askotan egon daitezke antolatuta. Antolakuntza-modu bakoitzari “mikroegoera” izena eman diezaiokegu. Sistema makroskopiko bat, hasiera batean, erabat definiturik irudika dezakegu. Hau da, mikroegoera posible guztietako batean dago. Sistemak eraldaketa bat jasatean, ikuspegi makroskopikoarekin bateragarriak diren mikroegoera anitz egiten zaizkio fisikoki irisgarriak. Mikroegoera horiek guztiak osagarriak dira, hots: fisikoki posibleak, batetik, eta ikuspegi makroskopikotik bereizezinak, bestetik. Mikroegoera posibleen areagotzeak entropiaren igoera etengabearen joera berdina duenez, Boltzmannek bien arteko proportzionaltasunean oinarriturik eman zuen entropiaren bere definizioa. Hala, partikulen antolakuntza-modu gero eta ugariagoen arteko bereizezintasun makroskopikoa litzateke entropia. Horratx desordena.

Hamarkada batzuk geroago, Claude Shannon ingeniariak ezjakintasunaren kontzeptua gehitu zion desordenaren metaforari. Komunikazio-sistemen teorizazioa egiten ari zen Shannon, eta, mezuek daramaten informazio-kantitatea modu matematikoan formulatu zuenean, Termodinamikan usu erabilia den entropiaren itxurazko adierazpenarekin egin zuen topo. Sistema bateko entropia-igoera, hala, sistema horri buruzko informazio-galerarekin lotu zuen. Eta, Boltzmannen ikuspegiarekin batera, egun darabilgun adiera arrunta garatu zen hala: entropia, sistema fisikoen inguruko ezjakintasun- eta desordena-maila adierazten duen magnitudea.

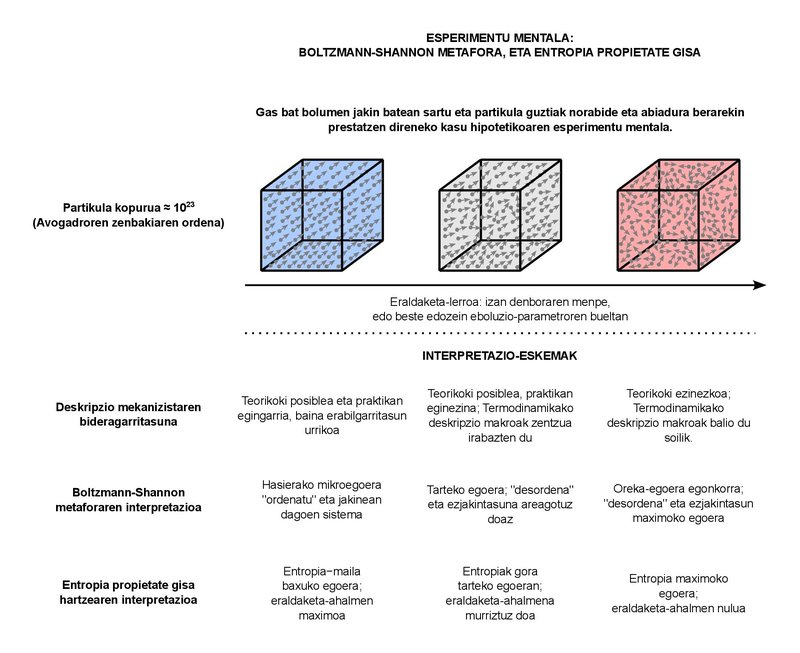
Ibilbide semantiko labur honen ostean, bi puntu baino ez. Lehena: adierazitako kontzeptuen esanahi kolokialak (energia, kontserbazioa, entropia) tentuz erabili beharrekoak dira. Beraien baliokide teknikoen ideia gakoa modu egokian islatu badezakete ere, ñabardura garrantzitsuak utz ditzakete kanpo. Eta bigarrena: Termodinamikako bi legeen esamolde arruntei horixe bera gertatzen zaie; alegia, legeek daukaten karga teknikoa lausotu egiten dutela nolabait. Izatez, energiaren kontserbazioa ez da lehen legearen formulazio bat, ondorioetako bat baizik. Berez, lehen legearen adiera abstraktuak zera dio: energia propietate fisiko gisa definitu daiteke. Hori litzateke berorren esanahirik sakonena.

Bigarren legearekin ere antzera gertatzen da. Kasinoaren irudia didaktikoa izan daiteke nolabait, baina ez da guztiz teknikoa. Formalki adieraztean, bigarren legeak oreka-egoera egonkorren existentzia baino ez du kodifikatzen. Sistema orok orekarako joera duela jazoera enpirikoa da. Bada, oreka-egoera guztien artean, bigarren legeak zera dio: sistema deskribatzen duen magnitude-multzoak hartzen duen balio bakoitzerako oreka-egoera egonkor bakarra dagoela. Bi legeak uztartzeak dakarren ondorio zuzena, hala, hauxe da: entropia magnitudea, energiaren gisan, propietate bat da; hain zuzen ere, sistema bat bere oreka-egoera egonkorrera iritsi dela adierazten duen propietatea, har dezakeen balio maximoa agertzen baitu entropiak egoera horretan.

Energia eta entropia, beraz, ez dira horren desberdinak. Propietate fisikoak dira biak, hots, edozein sistemaren egoera fisikoa deskribatzeko erabil daitezkeen magnitudeak. Oinarrizkoenak, bide batez; izan ere, bi legeetatik modu zuzenenean eratorritakoak dira. Eta, propietate gisa, modu egokian daude definituta sistemaren egoera guztietarako, izan oreka-egoerak edo orekatik kanpo daudenak, egonkorrak edo ez. Are gehiago, eta energiaren kontzeptuarekin gertatzen den moduan, entropia ez da magnitude estatistiko edo informazional bat, alor horietan bere adierazpen propioak hartzen baditu ere.

Propietate gisa, energiak sistema batek dituen elkartruke-ahalmenak kuantifikatzen ditu; entropiak, aldiz, eraldaketa-ahalmenari erreparatzen dio. Zenbat eta entropia gehiago, orduan eta eraldaketa-ahalmen urriagoa. Oreka-egoera egonkorrera iristean, entropiak balio maximoa hartuko du, eta eraldaketa-ahalmena nulua izango da. Desordena maximoa eta ezjakintasun totala baino, ordena perfektua eta sistemaren gaineko jakintza guztia izango dugu: izan ere, ezingo da oreka-egoera egonkor hori ez den beste batean egon.