Nombre d'or

1992/09/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

«... deux choses ne peuvent pas être combinées sans tiers, il faut un lien qui les unit, et il n'y a pas mieux que soi-même et ce qui réunit, tout égal et unique. Et la nature de la proportion atteint cet objectif, puisque de trois nombres, ou de trois masses, ou de l'une des trois forces, la proportion par rapport au dernier est la même que par rapport au dernier, et, d'autre part, lorsque la proportion par rapport au dernier est la même qu'avec le premier d'entre eux (le médian devient le premier et le dernier au milieu), tous restent intentionnellement comme avant, faisant partie d'une relation similaire.»

Platon, “Conversations, Timée”

L'origine du nombre d'or est ancienne. On ne peut pas savoir depuis quand l'homme connaît (apika, harean pentagramme, makila sans soulever, qu'il pouvait imaginer depuis qu'il était conscient). Les Égyptiens le connaissaient déjà, mais c'est Euclide qui le définit:

« Un droit est divisé en proportion entre les têtes et la bisectrice lorsque la proportion entre la plus grande et la plus grande est la même entre celle-ci et la plus petite. »

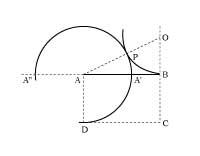
Par exemple, dans la figure 1, la partie AA' est le segment or ou la section du segment AB,

AA' = A'BAB = AA'

La proportion est remplie.

Si le lecteur ne pense pas qu'il vérifie une règle. Indépendamment du segment AB,

AA'

= = = = = = = = = = = = = = = = = = = =

A'B

? AB = AA' = ?

le rapport donnant la section d'or prend toujours la même valeur :

d = 0,618033988

C'est un nombre algébrique irrationnel d dont l'expression concrète est:

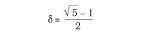
Ce nombre nous surprend dans l'Antiquité, dans la Renaissance et aujourd'hui.

Nous allons mentionner deux propriétés curieuses:

Si à d on ajoute 1 ou on retourne, on obtient la même valeur :

1 + ? = 1 / ? edo1 + 0,618033... En soustrayant = 1,618033 = 1 / 0,618033...1-i ? ou en calculant ?2, nous obtiendrons la même valeur :1 – ? = ?2 edo1 – 0,618033... = 0,391966... = (0,618033...)2

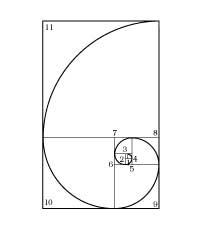
Depuis l'antiquité, on connaît les méthodes de division d'un segment en proportion d'or (1. irud. ). La proportion d'or se trouve également dans de nombreuses figures géométriques.

Le plus connu est la portée (ou étoile à cinq sommets), symbole magique des pythagoriciens et alchimistes (2. irud. ). Bien que la Renaissance a donné une grande importance à la proportion d'or, à la fois en théorie et en pratique, il n'a pas été utilisé pour la première fois à la Renaissance. En revanche, dans la pyramide de Khéops (3. irud. ), déjà utilisé au Parthénon d'Athènes, Cathédrale de Chartres, etc.

Figure . Pentagramme ou étoile à cinq sommets inscrite au Pentagone. La principale et la plus magique des figures dorées. Dans ses dimensions relatives est basé le nombre d'or:

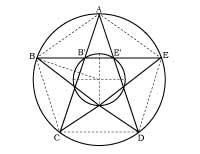
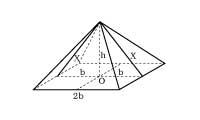
Figure . Selon le géographe grec Hérodote, qui a décrit les pyramides égyptiennes, la taille h de la pyramide de Khéops est la moitié de la base b et la moitié de l'apothème x. C'est-à-dire,

Cela signifie que la section acide de b x et donc le périmètre de la base est égale à la longueur de la circonférence de hauteur h. C'est pour cette raison que certains Egyptiens croyaient connaître le tableau du cercle. Il n'est pas nécessaire de recourir aux Atlantiques ou Martiens. Le secret de la grande pyramide réside dans ses dimensions d'or :\ e 4

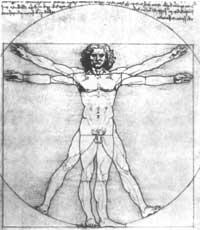
Il se trouve également dans le corps humain lui-même. Selon le “canon” de Léonard, les proportions les plus belles et harmonieuses du corps sont obtenues quand elles sont en proportion dorée. Léonard a mis l’“homme brillant” dans un cercle dont le centre est le même et dont le rayon est dans une proportion dorée avec la hauteur de l’homme (4. irud. ).

Les scientifiques de la Renaissance adaptaient au nombre d'or la valeur de la loi universelle de l'harmonie. Ils ne se trompaient pas, XVII. Comme l'a montré Kepler au XXe siècle. Les proportions d'or apparaissent sur les distances entre les planètes. Le nombre d'or indique quand une année spécifique correspond à un cycle lunaire de 19 ans.

La section d'or se trouve aussi dans la nature et ses phénomènes. On trouve souvent des fleurs et des plantes aux proportions d'or. Parmi les animaux il y a aussi des exemples: l'étoile de la mer, la coquille du fossile animé Nautilus (5. irud. ). L'atome de carbone, c'est-à-dire les diamants et le composé de base des êtres vivants, a aussi une structure d'or.