Raúl Ibáñez Torres: "La géométrie offre de nouveaux outils pour mieux représenter les cartes"

Mais c'est une vision pessimiste. Mais j'ai une vision positive. La géométrie offre de nouveaux outils pour une meilleure représentation des cartes. Je ne pense pas que ce soit une source de frustration. Il est vrai que la géométrie dit que vous ne pouvez pas faire une carte parfaite de la Terre - d'une sphère, en bref -. Mais les gens ne pensent pas ce que cela signifie. Cela signifie qu'une carte doit maintenir les caractéristiques qui nous intéressent. Qu'utilisons-nous sur une carte ? Distances, chemins plus courts, surfaces, directions, angles, etc. Nous voulons que les cartes gardent tous. C'est un problème de mesure, de mesure. Nous voulons apporter les caractéristiques métriques d'une sphère à un plan, ce qui est ce que la géométrie estime impossible.
XVIII. Au XXe siècle, Euler l'a montré avec une belle et simple preuve. Si je prends une balle et que je la casse en deux, et que j'essaie de convertir une moyenne en plat, je la plierai ou je la casserai. Ou inversement, si vous essayez de coller un sceau sur la peau d'une orange, le sceau sera ruiné. Cela montre qu'il est impossible de faire une carte parfaite. Et si c'est impossible, quoi ? Nous devons faire des cartes qui gardent les caractéristiques les plus importantes.
La carte de Mercator prit une grande importance à l'époque des grands voyages, car elle gardait les directions des parcours, un must dans la navigation. C'est pourquoi elle a été si importante pendant des siècles. C'est pourquoi et pour une autre raison: dans les territoires proches de l'équateur (version classique) la carte présente une distorsion très faible. Par conséquent, sur des cartes de très petits territoires, la projection est très importante.
Concrètement, pour la réalisation de cartes d'Euskadi ou de petits territoires on utilise la projection appelée UTM. Beaucoup de ceux qui travaillent en cartographie ne savent pas ce que cela signifie, mais demandent au logiciel d'utiliser UTM. UTM signifie Universal Transverse Mercator, projection transversale universelle de Mercator. C'est une projection adaptée de Mercator.

En d'autres occasions, cependant - lorsque nous faisons des peintures murales ou représentons des questions scientifiques, ou pour la distribution des langues du monde, ou pour diverses cartes de vulgarisation, ou pour des cartes didactiques -, nous avons besoin de cartes qui soutiennent les surfaces ou qui déforment très peu les surfaces. Ces cartes nous informent des territoires et de ce qui y est. Il y a beaucoup de cartes de la même surface, comme celle de Lambert.
Par exemple, ceux qui soutiennent les routes les plus courtes. Dans eux on utilise la projection centrale. C'est une projection très utilisée dans la navigation maritime et aérienne. Il est important d'utiliser la géométrie pour sélectionner les cartes les plus appropriées. C'est ce qui a été fait dans l'histoire. Un bon exemple est celui du premier pilote à traverser l'Atlantique en avion et seulement en 1927, Charles Lindberg. Pour pouvoir faire le vol, je devais savoir par où aller. Projection de Mercator pour maintenir la direction qui l'intéressait. Mais avec cette projection, je devais beaucoup dévier et j'étais obligé de parcourir un long chemin. C'est pourquoi Mercator a utilisé avec une autre projection, celle qui gardait les routes.
La distorsion minimale est en Équateur. Mais la projection UTM est utilisée en remplaçant l'équateur par un méridien et parallèle, selon le territoire que vous souhaitez représenter sur la carte. Près de ce point, la projection est très bonne. C'est pourquoi l'UTM est utilisée. Dans les images satellites, par exemple, la projection UTM est adaptée à la trajectoire du satellite.
Par ailleurs, de nombreuses images par satellite ne sont pas des photos. Ce sont les balayages des données, qui sont conduites à une projection géométrique et qui constituent des cartes communes. Puis ils ajoutent des couleurs pour lui donner un aspect réaliste.

Les cartes n'ont pas beaucoup changé, mais l'utilisation de cartes, car aujourd'hui, nous pouvons savoir où nous sommes en temps réel.
C'est un sujet très controversé et de précaution. Beaucoup de gens ont cru à une fausse histoire parce qu'ils ont donné une touche solidaire à la carte. Mais si cela est dit, les gens se sentent agressés.
Peters est cinéaste, historien, journaliste et fait une thèse sur la propagande politique. C'est important. En 1967, il a présenté une carte, mais il y avait un autre comme cent ans auparavant. Elle a été réalisée par un clerc nommé James Gall. Je ne sais pas si Peters le connaissait ou non, mais imaginons que non. Les scientifiques lui ont dit que cette carte n'était pas nouvelle. La science accepte parfois des choses qui ne sont pas nouvelles, mais seulement quand elles ont de nouvelles contributions. La carte de Peters n'avait pas de nouvelles contributions.
En 1973, il réalise une conférence de presse dans laquelle il présente la carte de Mercator comme la seule alternative au "raciste". Il a dit que seules deux cartes existaient, celle de Mercator et la sienne, et que c'est la seule carte qui soutient les surfaces. Ce n'est pas vrai. Il y a beaucoup de cartes qui soutiennent les surfaces. Par exemple, la carte azimutale de Labert, la carte sinusoïdale de Sanson-Flamsteed, la carte conique d'Albers, celle d'Eckert, etc.
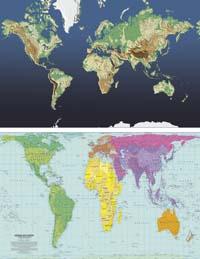
Celui qui ne connaît pas tout cela se convainc facilement parce qu'il est impliqué dans de nombreuses idées sur le tiers monde : le thème de la faim, du colonialisme, etc. Les médias se sont rapidement positionnés en faveur de la carte de Peters et la polémique a émergé. Les cartographes ont essayé de transmettre la vérité, mais personne ne les a valorisés. Par la suite, de nombreuses institutions religieuses, la plupart catholiques, et de nombreuses ONG se sont mises en faveur de l'idée de la carte, même l'UNESCO elle-même clairement, sans aborder le sujet du point de vue scientifique, géométrique et cartographique. Elle est devenue une icône de thèmes de solidarité. Et Peters a vendu la carte.
Beaucoup disent qu'il a la même chose, qui est en définitive une carte qui maintient les surfaces. Et donc, mais pour beaucoup de choses, il ne convient pas, car il déforme beaucoup les formes. Je pense que changer un mensonge pour une autre ne va pas bien. Il faut faire une réflexion raisonnable. Comme le firent National Geographic, ils utilisent de nombreux types de cartes, mais ils utilisent la projection Winkel Tripel pour montrer des cartes du monde. Il ne résiste rien (ni surfaces, ni trajectoires, etc. ), mais la distorsion est très faible dans toutes ses caractéristiques. Il montre très bien les formes, ce qui en fait une bonne carte. Une bonne réflexion.
Le Gouvernement basque et plusieurs institutions, dont la Fondation Elhuyar, ont également publié et distribué la carte de Peters dans les écoles. Il me semblait offensant. On pourrait penser que Peters est de bon cœur, mais si vous lisez votre livre il y a beaucoup de mensonges et de manipulations (je recommande beaucoup de lire, mais avec une attitude critique). C'est inquiétant.

Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian











