Barrejat (II)

1991/07/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Amb motiu de les vacances hem volgut portar a aquest número un nou regirat. A l'espera que aquests dies tinguis temps, hem preparat 50 qüestionaris perquè puguis omplir aquesta beta. Com en l'anterior, aquí també pots trobar de tot: la lluna, la vaca, els poxpolos, els quadrats, les divisions, els somnis, les oques, els ulls, els rectes, ........................................................................................................................................................................................................... En general, si no són de broma, no et fiïs, et pots marejar.

1. Si la persona fos invisible, ho veuria?

L'ull que et portes no és
perquè el veus tu, és
perquè et veu l'ull.

(Antonio Machado)

2. Una persona veu l'ós i es desplaça cap al sud corrent 10 km. Des d'allí ha recorregut altres 10 km a l'est i, finalment, altres 10 km al nord. Mira on i el mateix ós torna a veure'l. De quin color és l'ós?

3. Tenim vuit monedes aparentment iguals, però una té menys pes que unes altres. Es pot saber quina és la moneda fent només dos pesos?

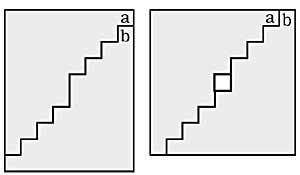
4t Quin signe cal posar en el requadre buit? (Figura 1)

5. Es produïa en un poble situat a la frontera entre els estats d'Ibaibusti i Mendiberdea. Una lliura d'Ibaibusti costava 90 cèntims d'una lliura de Mendiberdea. Així mateix, una lliura de Mendiberde a 90 cèntims d'una lliura d'Ibaibusti. Un dia, una persona va entrar en un bar de la zona d'Ibaibusti i va demanar un suc de 10 cèntims va pagar amb una lliura local. Al seu retorn, en lloc de donar 90 cèntims d'Ibaibusti, li van donar una lliura de Mendiber-d. Més tard es va traslladar a un bar de Mendiberde i quan va demanar un vímet de 10 cèntims va pagar amb l'allibera anterior, retornant 90 cèntims a una allibera d'Ibaibusti. D'aquesta forma es va desplaçar una vegada i una altra d'un bar a un altre. Finalment, després de beure tot el que es volia, va tornar a casa amb els diners que tenia al principi. Qui va pagar els vímets?

6è Posa en tres piles 11, 7 i 6 monedes. En tres moviments has de deixar vuit monedes en tres munts. En els moviments, a cada pila se li pot afegir tantes monedes com tingui i aquestes monedes han de procedir del mateix munt.

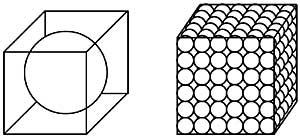
7. Tenim dues caixes cúbiques iguals. En un d'ells hi ha una bola de ferro de diàmetre igual a l'altura de la caixa; en l'altre, com es veu en la imatge, hi ha les mateixes boles de ferro. Quina caixa té més pes? (Figura 2)

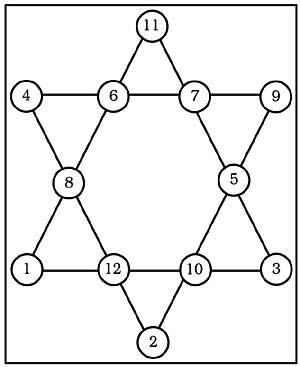
8è. L'estrella de la figura 3 és màgica, ja que la suma dels quatre números de les seves sis línies són 26. No obstant això, la suma dels números dels seus vèrtexs és de 30. Podria solucionar-ho per a aconseguir una superestrella màgica, és a dir, que la suma dels vèrtexs també sigui 26?

9. Com es pot solucionar el següent producte que està malament sense afegir, llevar o escriure res?

81. 9 = 801

10. Quina és la ruta més curta per a passar d'a B per sobre de la superfície de la galleda? (Figura 4)

11. Aquest succés va tenir lloc en un poble anglès, en el matí i a l'església d'un diumenge. El sacerdot treballava en el seu sermó, com sempre. El sol cremava. A causa del silenci que hi havia en el seu interior i al rumor llunyà del carrer, Peter es dormió. En temps de la revolució francesa somia que portaven a la gilotina. Portaven en un carro i la gent li insultava. Va arribar al botxí i li van col·locar el cap sota el ganivet. Quan Aifría queia sobre el seu coll, es va adonar que la seva dona estava adormida i es va colpejar un petit cop de ventall en el coll. L'emoció va provocar la mort del pobre Peter. Quina és la raó lògica per a qüestionar aquest episodi?

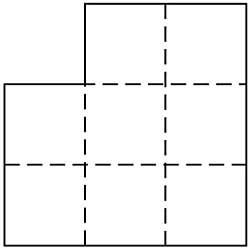
12. Has de dividir la imatge en tres parts, recollint-la adequadament per a obtenir un quadrat concret. (Figura 5)

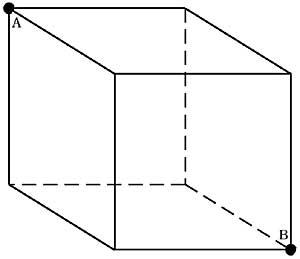
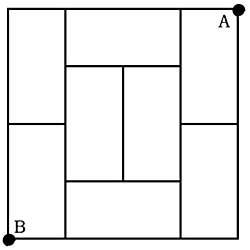
13. Una habitació està plena de vuit tatamis, tots ells de 2x1 metres. Caminant per les vores dels tatamis, quin és el recorregut més llarg entre els punts A i B? (no es pot passar dues vegades per les vores). (Figura 6)

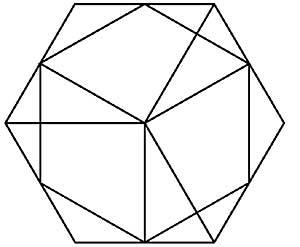
14. En la figura 7 pots veure un altre cub dins d'un cub. Estàs segur que així és?

15. Imagina't que condueixes un autobús. En la primera estació han pujat 5 viatgers. En la següent han pujat 5 i han baixat 7. El tercer puja 3 i no baixa cap. En els següents s'han pujat i baixat 8 i 5, 2 i 6, 7 i 4 respectivament. Quants anys té el conductor?

16. Les 15 boles del billar americà es col·loquen formant un triangle equilàter. Mirant per un vèrtex, podries col·locar cada bola de manera que tingui la diferència de les seves dues boles tangents de darrere?

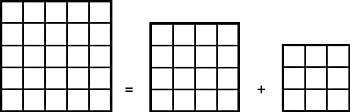
17. Has de dividir un quadrat de 5x5 en quatre parts, de manera que formin quadrats de 4x4 i 3x3. (Figura 8)

18. Si un rellotge de carilló triga 2 segons a tocar les dues hores, quant trigarà a sonar les tres?

19. La lletra M es talla amb tres rectes per a obtenir nou triangles. (Figura 9)

20. Que no! No dibuixar un quadrat amb dues rectes!

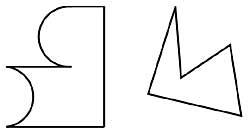
21. Dividir les dues figures laterals formant dues peces iguals en cadascuna d'elles. (Figura 10)

22. Com dividir el quadrat de la figura 11 en quatre parts de la mateixa grandària i aspecte, cadascuna amb una estrella i un cercle?

23. En un grup una persona diu: “el meu germà va morir fa 130 anys”. Pot ser cert?

24. En moure dos poxpolos es pot aconseguir que les vaques mirin cap endarrere. (Es permet que la cua quedi a dalt o a baix) (Figura 12)

25. Entre dues monedes de cinc duros i pegades es col·loca una dura. Cal llevar el duro sense moure's pel centre.

26. Tira deu monedes a tres boscos deixant en cadascun un nombre imparell de monedes.

27. Ara dos exercicis més sobre imatges màgiques:
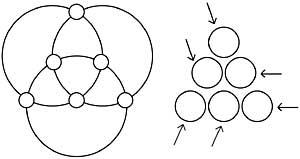
Escrigui els números 1, 2, 3, 4, 5, 6 en cercles blancs perquè les sumes dels números de la mateixa circumferència siguin iguals.

Escriu ara els números 1, 2, 3, 4, 5, 6 perquè la suma dels números de les línies que ens marquen les fletxes siguin diferents i successius valors. (Figura 13)

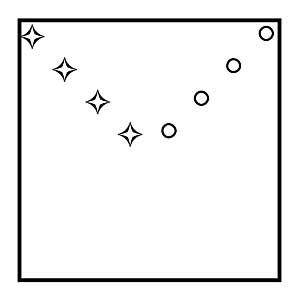
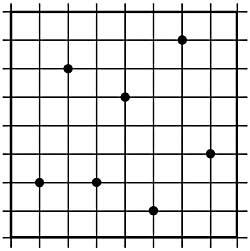
28. Agrupi correctament els set punts marcats en la taula de la figura 14, envoltant la menor superfície possible. No es poden tallar entre si.

29. Copiï la imatge següent en un paper i retallada per la línia en pols. Uneix les dues peces obtingudes com es pot apreciar en la figura 2. Els rectangles de les figures 1 i 2 tenen la mateixa longitud. Per tant, tenen la mateixa superfície. No obstant això, el segon rectangle té una superfície menor, en faltar-li el quadrat central. Quina és l'explicació d'aquesta paradoxa? (Figura 15)

30. S'han adonat que les dones d'un poble són enganyades pels seus veïns, almenys un, i han traslladat la seva queixa als seus representants.

Els representants, una vegada localitzats els veïns deslleials, decideixen enviar una carta a les dones. En ella apareixen els noms dels veïns deslleials, excepte la de la dona a la qual s'envia la carta, que pot haver enganyat, però potser no. Els representants han autoritzat les dones a castigar públicament als deslleials veïns descoberts. Per a encertar la veritat, les dones compliran dues condicions: una és no parlar entre elles i una altra és que només puguin veure si hi ha algun veí deslleial castigat o no a la nit.

Passat el primer dia no hi ha hagut cap càstig, ni després del segon. Així fins a la nit dels cuarentamarga, en la qual tots els veïns deslleials han estat castigats. Quants veïns han enganyat a les dones?

31. Un adult i una nena han de travessar el riu; un d'esquerra a dreta, l'altre a l'inrevés. En cada riba hi ha una taula, però ambdues una mica més curtes que l'amplària del riu. Què poden fer l'adult i la nena per a travessar el riu?

32. Escriu 64 utilitzant només dos quatre. Pots utilitzar els símbols matemàtics que vulguis, però en cap cas més números.

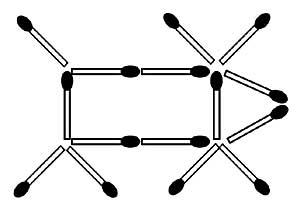
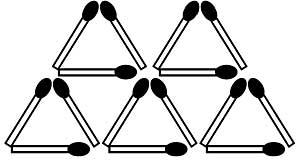
33. Movent només dos poxpolos pots substituir els set triangles equilàters de la figura 16 per cinc. Ho aconseguiràs?

34. En el seu llibre “Logika jokoa”, Lewis Carroll va escriure les següents frases:

• Cap oca balla
• Cap militar pot deixar de ballar el vals cada vegada que pot
• Tots els ocells de la meva barrera són oques

Quines conclusions lògiques pots extreure d'aquestes tres frases?

35. Quins són els criteris de les següents sèries numèriques? :

a) 1, 3, 5, 15, 30, 40, 50, ... b) 6, 8, 62, 63, 66, 72, 73, 76, 81, 84, ... c) 1, 101, 31, 131, 131, 1131,

2131 d) 1, 9, 2, 2, 5, 3, 4, 7, 8) 6, 2, 5, 5, 5, 4, 6, 6, 7, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 7, 6, 6, 6, 6, 6, 7, 6, 6, 6, 6, 6, 6, 6, 2, 6, 6, 6, 3, 6, 6, 2, 3, 6, 3, 3, 3, 3, 3, 3,

3, 3, 7, 3, 7, 6, 6, 6, 3, 3, 6

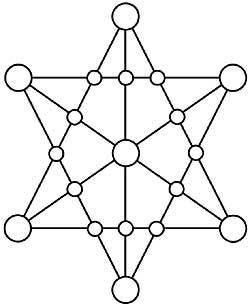
36. Localitzi els números 1 al 19 en els cercles d'hexagrama de la figura 17 perquè les sumes dels cinc números de cada línia siguin iguals.

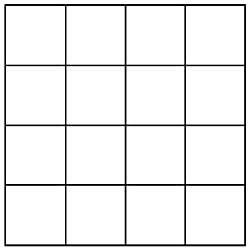
37è Podries completar 9 línies de 5 monedes si només tens 21 monedes?

38è Es pot fer la següent imatge sense aixecar el bolígraf del paper i passar dues vegades per sobre d'una ratlla? (Figura 18)

39. Un savi vol mesurar el temps de caiguda d'un objecte alliberant-lo d'un ascensor que puja. En el 5è pis, i després de deixar caure, el petit objecte verd queda a dos passos de l'investigador surant en l'aire. Quins motius va trobar el savi per a explicar aquest increïble succés?

40. Com situaries 5 monedes?

41. Després de cinc punts, com associaries cada punt amb altres dos punts mitjançant correctors? De quines formes es pot fer?

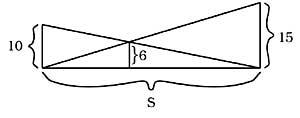
42. Quina és la longitud de S sense càlcul? (Figura 19)

43. Una per a respondre molt ràpid. Un pastor té 17 ovelles. Si tots marxen menys de nou, quants han quedat?

44è Estareu d'acord si una frase és falsa dient que és veritat la seva contrària, no? Per exemple, “Aquesta frase té sis paraules”, evidentment és mentida. El contrari serà “Aquesta frase no té sis paraules”, però també és mentida. Què opines?

45. Multiplicant un número de dues xifres pel doble de 2 obtenim 3. Quin és el número?

46. A continuació es mostra un altre tipus de divisió. Has de dividir la lluna en sis parts per dues rectes. Quadrada en vuit triangles aguts. I finalment, la creu amb dues línies rectes, una passant per a i l'altra per B, per a poder formar un quadrat amb les peces que queden. (Figura 20)

47. En una habitació hi ha tres savis i cinc barrets (tres blancs i dos negres). Per un moment s'apaga la llum i es col·loca un barret blanc als caps dels erudits, els dos barrets negres han sortit sense ser vists pels savis. De seguida s'ha encès la llum. Cada savi pot veure els barrets dels altres, però no el seu. Els pregunten el color del barret que porten. Per un moment es miren i finalment un diu: el meu és blanc. Per què ha encertat?

48è. En una nació de deu països, cada any els recaptadors de cada país havien de donar 10 unces d'or a l'Estat. Un any un recaptador va voler guardar una mica d'or. Per a això va ordenar eliminar un gram de cada adoberia, conservant l'aspecte de la beina. Però un jutge va ser avisat amb tota precisió per a anar amb compte amb la recaptació d'aquell any, perquè un recaptador volia enganyar.

El jutge va ordenar que tots els recaptadors s'emportessin tots els abonaments a la mateixa hora del mateix dia. Va demanar una balança que pesava grams per gram i després de fer una pesada davant tots, va posar en evidència a l'estafador. Com ho va saber?

49è Les monedes de l'esquerra de la figura 21 han de situar-se en tres moviments com en la imatge de la dreta, respectant dues regles

a)

en cada moviment es mou una moneda sense canviar les altres,

b)

les monedes sempre han de tocar altres dues monedes.

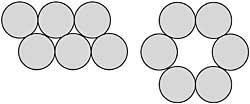
50. Amb un moviment has de formar dues línies de quatre monedes. (Figura 22)

Tens un mes per a respondre a aquestes preguntes. T'esperem al setembre. Si no pots resoldre alguna, explica'ns la teva solució. Tenim tots. No hem publicat les preguntes ni les respostes en el mateix número perquè no ens sembla convenient. No obstant això, estem disposats a donar totes les explicacions en la pròpia revista o d'una altra manera.