Musa, zoria ala jakituria?

Sarrera

Musa, euskaldunon jokoen jokoena, ez dugu guk hemen deskubrituko. Gure helburua ez da ezer berririk asmatzea. Azterketa matematiko (probabilistiko) txiki bat egiten saiatuko gara ordea. Zorizko joko guztietan bezala, zoriak eragin handia dauka, baina jokoa zuzena bada, guztiok izan behar dugu zori berbera. Beraz, zoriaz aparte jakituria eta esperientziak asko balio dute.

Artikulu honetarako pare eta puntuen probabilitateak, (lau zein zortzi erregetan), kalku latu ditugu eta horietan oinarrituko gara. Ez ditugu lau jokalarien probabilitate bateratuak kontutan hartu; ezta, mus eman eta gero, kasuen probabilitateak ere. Beraz azterketa oso azalekoa izango da.

Arauak

Lau jokalari bi bikotetan tartekatuak.
Launa karta banatzen dira.
Karten ordena batekotik erregerainokoa da.
Lau atal: handia, txikia, pareak eta jokoa (edo puntua), banaturik jokatzen dira:

• handia: kartarik altuenak (erregeak, zaldiak, txankak, .... )
• txikia: kartarik baxuenak (batekoak, bikoak, hirukoak, .... )
• pareak: karta berdinak pareak bi karta berdin mediak hiru karta berdin dupleak bi bikote edo lau karta berdin
• jokoa: karten balioak batzen dira puntua: 30 edo gutxiago, lehentasuna: 30, 29, 28, ...... jokoa: 30 baino gehiago, lehentasuna: 31, 32, 40, 37, 36, 35, 34, 33
  
  a) Kartak banatu eta gero jokalariek mus dagoen ala ez banan-banan esan behar dute, eskutik hasiz.
  b) Mus badago, jokalariek nahi dituzten kartak gorde eta besteak (gutxienez bat) aldatu egin ditzakete. Berriro a) puntura.
  c) Musik ez badago, kartak ezin dira aldatu.
  d ) Lau ataletan apostuak egiteko sistema bera da: jokalariek enbido jo edo paso egin dezakete (ordena gordez); bikote batek enbido joz gero, besteak hiru aukera izango ditu:

eduki (nahi), kasu honetan eskualdi amaieran ikusiko da zeinek irabazten duen;
ez eduki (ez nahi), kasu honetan enbido jo duen bikoteak puntu bat hartuko du;
gehiago jo, hots apostua igo. Kasu honetan beste bikoteak berriz hiru aukera izango ditu: eduki, ez eduki edo gehiago jo. Oraingoan, azkeneko apostua edukiz gero, eskualdi amaieran ikusiko da irabazlea zein den, edo bikote batek atzera eginez gero (ez eduki), besteak ordurarteko apostuko puntu guztiak jasoko ditu.

e) Enbidoa bi puntu da. Apostua nahi bezain handia izan daiteke, baina jokaldi osoa apostu egiteko hordago jotzen da.
f) Paretara eta jokora enbido jo baino lehen parerik edo jokorik zein jokalarik daukaten jakin behar da. Enbido jo ahal izateko gutxienez bikote desberdinetako jokalari banak eduki behar du parerik edo jokorik. Lau jokalariek jokorik ez badute puntutara jokatzen da.
g) Handira, txikira eta dagokionean puntura paso emanez geratuz gero, amaieran irabazten duenak puntu bana jasoko du. Paretara eta jokora paso emanez gero ez da punturik hartzen. Hala ere, parerik edo jokorik onena duen bikoteak jasotzen ditu puntuak:

paretakoak pareak = 1
mediak = 2
dupleak = 3

jokokoak 31 puntu = 3
gainerakoak = 2

Puntura bikote batek enbido jotzen badu eta besteak edukitzen ez badu, lehenengoak bat ez eta bi puntu jasotzen ditu.

h) Jokaldiak 40 puntura (batzuetan 30 puntura) jokatzen dira.
i) Arau hauetan lau errege eta lau bateko daude. Badago, aldiz, jokatzeke beste aukera bat, bikoak batekotzat eta hirukoak erregetzat hartuz, hau da, zortzi errege eta zortzi bateko edukita: batekoak (bateko eta bikoak), lau, bost, sei eta zazpikoak, txankak, zaldiak eta erregeak (erregeak eta hirukoak).

Hiztegitxoa

Joko guztiek bezala, musak ere bere hiztegi berezia dauka. Hona hemen oinarrizkoa.

Kartak banatutakoan, musik dagoen ala ez erabaki behar denean:

Esku: kartak banatu dituen jokalariaren eskuinean dagoena.
Postre: kartak banatu dituena.
Mus: jokalariak zenbait karta aldatu nahi du.
Ez dago musik: jokalariak ez ditu bere kartak aldatu nahi.
Eskuarekin: esku denaren bikotekidea bat dator eskuarekin. Oro har mus dagoela esan nahi du.
Hara: postrearen bikotekideak postreari pasatzen dio erabakia (mus ala ez).

Musik ez dagoenean:

Paso, ba: jokalariak ez du aposturak egiten.
Enbido: bi puntu apostu egin.
Enbido gehiago, 7 gehiago: aurreko apostuari jokalariak 2, 7 gehiago eransten dizkio.
Hordago: jokalariak eskualdi osoa apostatzen du.
Onartuz gero, momentuan bertan ikusten da.
Eduki, nahi: jokalariak apostua onartu egiten du, eskualdiaren amaieran ikusiko da.
Ez dut nahi: jokalariak ez du apostua onartzen.

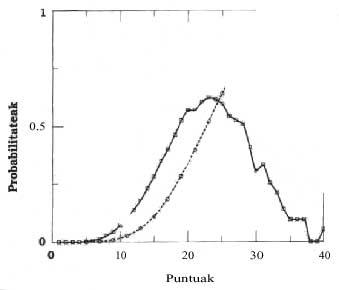
Lehenengo eta bigarren irudietan puntuen probabilitateak azaltzen dira, lau eta zortzi erregetara hurrenez hurren.

Lau erregetara punturik probableena 23 da 0,623 probabilitatearekin, horren bi aldeetara probabilitateak jaitsi egiten direlarik (lerro jarraia). Nabaria da 31 puntua, non probabilitatea pixka bat igo egiten den, gero jaitsi egiten delarik. 31 puntuaren probabili tatea 0,033 da.

Lehenengo irudian marra etena ere ikus daiteke. Marra eten horrek probabilitate metatuak azaltzen ditu. Adibidez, 23 edo puntu gutxiago edukitzeko probabilitatea 0,520 da. Lerro honek 30 edo puntu gutxiago izateko probabilitatea 0,871 dela esaten digu, edo bestela esan, jokorik izateko probabilitatea 0,128 dela.

Bigarren irudian, zortzi erregetarakoei dagokionean, lerro jarraiaren itxura guztiz aldatzen da. Nabarmenena, aldaketagatik eta jokoan duen garrantziagatik, 31 puntuaren probabilitatearena da, kasu honetan handiena 0,091 izanik. Beste aldaketa nabarmena, 22 puntuarena da; bere probabilitatea 0,086ra igotzen bait da. Jokoan, 40 puntuaren probabilitatea ere nabariro handitzen da.

Lerro etenak, kasu honetan, jokorik ez egoteko probabilitatea 0, 732 dela eta egoteko probabilitatea 0,267 dela esaten digu.

Taulen azalpena

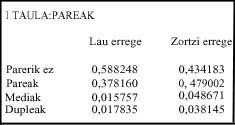
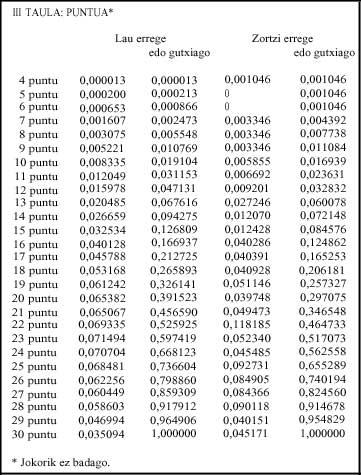
1. taula: taula honetan pare-mota bakoitzaren probabilitatea agertzen da, lau zein zortzi erregetan. Kasuak bereiztuak dira, hau da, jokalari batek mediak baditu, parerik badauka ere media bezala soilik hartuko dugu. Dupleak dituenean, gauza bera.
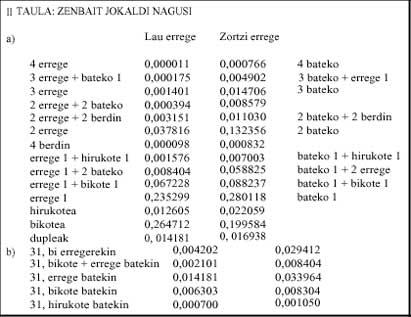
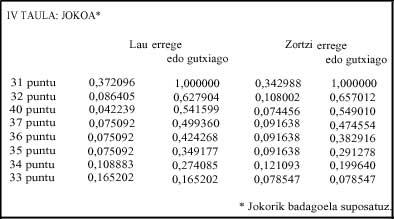
2. taula: oraingoan jokaldi nagusi batzuen probabilitateak ikus ditzakegu. Kasu hauek ere bereiztuak dira. Esate baterako, bi erregeren kasuan ez da sartzen bi errege eta bi bateko kasua.
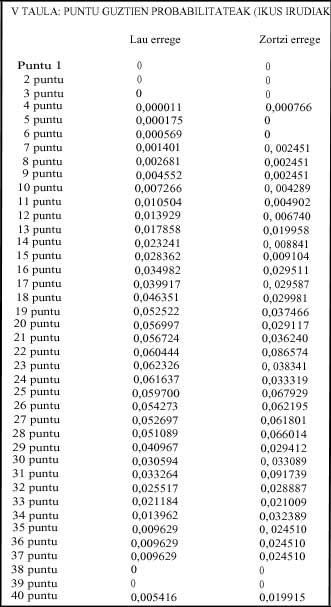
3. taula: jokorik ez badago, hots, puntuan, puntuen probabilitateak agertzen dira.
4. taula: jokorik badagoela kontsideratuz, jokobakoitzaren probabilitatea azaltzen da.

Iruzkinak

Lau erregetara parerik ez edukitzearen probabilitatea (0,588), edukitzearena baino handiagoa da. Zortzi erregetara, aldiz, ez edukitzearena (0,434) txikiagoa da (I taula).

Ohar gaitezen zortzi erregeko musean medien probabilitatea, 0,048 (I taula), dupleena, 0,038, baino handiagoa dela. Lau erregeko musean, ordea, dupleena, 0,017, mediena, 0,015, baino handiagoa da. Honek zortzi erregeko musa bestea baino zuzenagoa dela esaten digu; probabilitate txikiena duen kasua gehiago baloratzen bait da.

Jokorik egoteko probabilitatea, lau erregetan 0,128 da eta zortzi erregetan 0,267.

Jokoan alderantziz gertatzen da. Zortzi erregeko musean 31ren probabilitatea izugarri handiagotzen da (0,091) laukoarekin alderatuz (0,033). IIb taulan ikus daitekeenez, 31 lortzeko agertzen diren konbinazio guztien probabilitateak txikiagoak dira lau erregeko musean zortzikoan baino. Beraz, lau erregeko musa zuzenagoa dela esan genezake.

Lau erregetara, jokalari guztiek 31 baino puntu gutxiago izanez gero, hots, jokorik ez badago, apostua irabazteko probabilitate erdia 22 punturekin lortzen da. Izan ere P(22 edo gutxiago) = 0,525 (III taula).

Jokoan, hau da, gutxienez bi bikoteetako jokalari banak 30 baino puntu gehiago badauka, probabilitate handiena 31k dauka, 0,033; joko guztien artean (31, 32, 40, 37, 36, 35, 34, 33) probabilitateen herena (0,372) (IV taula). Kasu honetan apostua irabazteko probabilitateen erdia 40 punturekin gainditzen da; P(40 edo gutxiago) =0,541.

Zortzi erregetara, jokorik ez badago, hau da, jokalari guztiek 4etatik 30eraino puntu badauzkate, 22 punturekin ez da ailegatzen apostua irabazteko probabilitatearen erdira.Hori 23 punturekin lortzen da: P(23 edo gutxiago) = 0,517 (III taula).

Jokorik egonez gero, 31rena probabilitaterik handiena, 0,091; jokoen artean 0,342. Azkenik, apostua irabazteko pro babilitateen erdia 40 punturekin lortzen da: P(40 edo gutxiago) = 0,549.

Amaitzeko, probabilitateek kasuak ez dituztela ziurtatzen eta, beraz, ezin zarela fidatu esan behar da. Hala ere, esperientziak bezala, lagundu egiten dute. Artikulu honetaz balia zaitezen eta hobeto jokatzen ikas dezazun espero dugu.