Mathematica (III)

3. Funtzio baten mutur baldintzatuak

• Enuntziatua

Askotan, funtzio baten muturrak kalkulatzerakoan, mutur horiek bete behar dituzten baldintzak ematen dizkigute. Hau da, emaitza batzuk bakarrik onartu beharko ditugu. Ondorengo adibidean, funtzio jakin baten mutur baldintzatuak Mathematica erabiliz nola kalkula daitezkeen ikusiko dugu.

• Ebazpenaren urratsak

Lehendabizi, funtzioaren mutur arruntak kalkulatuko ditugu, gero, mutur baldintzatuekin alderatu ahal izateko. Mutur baldintzatuak Lagrange-ren biderkatzaileen metodoa erabiliz kalkulatuko ditugu.

• Erabiliko diren aginduak

D: funtzio baten deribatua kalkulatzen du, emandako aldagaiarekiko.

Solve: ekuazioak ebazteko agindua da.

Union: zerrenden bildura egiten du, elementu errepikatuak ezabatuz.

/.: ezkerreko espresioari eskuinean adierazten zaion erregela edo erregela-multzoa aplikatzen dio.

Plot3D: funtzio baten hiru dimentsioko irudia egiten du.

ViewPoint: hiru dimentsioko irudia ikuspuntu jakin batetik bistaratzen du.

AspecRatio: grafikoaren ardatzen arteko proportzioa adierazteko aukera da.

DisplayFunction: grafikoa bistaratzerko ala ez aukera ematen du.

PlotRange: funtzioaren balioak grafikoan mugatzeko aukera ematen du.

Axes: grafikoen ardatzak irudikatu ala ez adierazteko ezaugarria da.

Boxed: hiru dimentsioko irudietan kutxa irudikatzen du.

RGBColor: grafiko baten irudiaren kolorea aukeratzeko balio du.

PointSize: puntuak irudian edukiko duen tamaina adierazten du.

Point: bi edo hiru elementuko zerrendak plano edo espazioko puntu bati egokitzen dizkio.

Show: osagai grafikoak bistaratzen ditu.

ParametricPlot3D: hiru dimentsioko grafikoa egiten du ekuazio parametrikoetatik abiatuta. Funtzio bezala adierazi ezin diren gainazalak irudikatzeko erabiltzen da.

BoxRatios: hiru dimentsioko grafikoen ardatzen arteko proportzioak adierazteko aukera da.

ContourPlot: hiru dimentsioko irudi baten maila-kurbak irudikatzen ditu.

ParametricPlot: bi dimentsioko grafikoa egiten du ekuazio parametrikoetatik abiatuta. Funtzio bezala adierazi ezin diren kurbak irudikatzeko erabiltzen da.

PlotStyle: irudiaren ezaugarri batzuk definitzeko aukera ematen du.

Graphics: ematen zaion datua irudika daitekeen elementu bihurtzen du.

Polygon: emandako puntuak poligono baten bidez lotzen ditu.

• Ebazpena Mathematica-ren bidez

g[x_, y_]:= y³ + x² y + 2x² + 2y² - 4y – 8

Mutur arruntak:

d1[x_,y_]:=D[g[x,y],x]
d2[x_,y_]:=D[g[x,y],y]

punegon=Solve[{d1[x,y]==0,d2[x,y]==0},{x,y}]
punegon=Union[punegon]

{{x Æ 0, y Æ -2}, {x Æ 0, y Æ -2}, {x Æ 0, y Æ -2},
{x Æ 0, y Æ 2/3}}
{{x Æ 0, y Æ -2}, {x Æ 0, y Æ 2/3}}

d11[x_,y_]:=D[g[x,y],{x,2}]
d22[x_,y_]:=D[g[x,y],{y,2}]
d12[x_,y_]:=D[g[x,y],x,y]

h1[x_,y_]:=d11[x,y]
h2[x_,y_]:=d11[x,y]d22[x,y]-d12[x,y]²

hess={1,h1[x,y],h2[x,y]}
hess /. punegon

{1, 4 + 2 y, -4 x2 + (4 + 2y) (4 + 6y)}
{{1, 0, 0}, {1, 16/3, 128/3}}

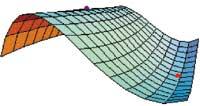
Lehenengo puntuan, (0,-2), zer gertatzen den ez digu esaten metodo honek, segidaren gai batzuk zero direlako. Beraz, ezin dugu erabaki puntu horren izaera. Bigarren puntuan aldiz, (0,2/3), funtzioak minimo erlatiboa du hessearren segidaren gai guztiak positiboak direlako.

p0=Plot3D[g[x,y], {x,-1,1}, {y,-3,1}, ViewPoint Æ {1,0.5,0.25}, AspectRatio Æ Automatic, DisplayFunction Æ Identity, PlotRange Æ All, Axes Æ False, Boxed Æ False]

-SurfaceGraphics-

mut=Graphics3D[{{RGBColor[0.5,0,0.5], PointSize[0.03], Point[{0,-2,g[0,-2]}]}, {RGBColor[1,0,0], PointSize[0.03], Point[{0,2/3,g[0,2/3]+0.1}]}}]

-Graphics3D-

Show[p0, mut, DisplayFunction:>$DisplayFunction]

-Graphics3D-

Mutur baldintzatuak:

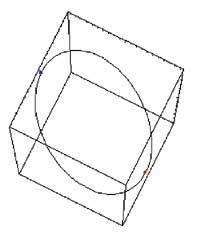
Baldintza: x²+y²=1

F[x_,y_]:=g[x,y]+l(x²+y²-1)

d1F[x_,y_]:=D[F[x,y],x]
d2F[x_,y_]:=D[F[x,y],y]
d11F[x_,y_]:=D[F[x,y],{x,2}]
d22F[x_,y_]:=D[F[x,y],{y,2}]
d12F[x_,y_]:=D[F[x,y],x,y]

pungel=Solve[{d1F[x,y]==0,d2F[x,y]==0,x²+y²==1}, {x,y, l}]

{{l Æ -(5/2), x Æ 0, y Æ -1},
{l Æ -(3/2), x Æ 0, y Æ 1}}

h1F[x_,y_]:=d11F[x,y]
h2F[x_,y_]:=d11F[x,y]d22F[x,y]-d12F[x,y]²

hessF={1,h1F[x,y],h2F[x,y]}

{1, 4 + 2y + 2l, -4 x² + (4 + 2y + 2l) (4 + 6y + 2l)}

hessF /. pungel

{{1,-3,21},{1,3,21}}

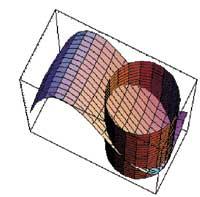
Beraz, lehenengo puntuan, (0,-1), minimoa du eta bigarrenean, (0,1), maximoa, hessearren segidaren gaien zeinuen arabera.

zi=ParametricPlot3D[{Cos[t], Sin[t], z}, {t,0,2þ}, {z,-10,0}, BoxRatios Æ Automatic, DisplayFunction Æ Identity]

-Graphics3D-

p1=Plot3D[g[x,y],{x,-1,1},{y,-3,1}, BoxRatios Æ Automatic, DisplayFunction Æ Identity]

Show[p1, zi, DisplayFunction:>$DisplayFunction,
ViewPoint Æ {1,0.5,8}]

-Graphics3D-

ps1=Graphics3D[{{RGBColor[1,0,0], PointSize[0.025], Point[{0,1,-9}]}, {RGBColor[0,0,1], PointSize[0.025], Point[{0,-1,-3}]}}]

-Graphics3D-

mb1=ParametricPlot3D[{Cos[t], Sin[t], -3Sin[t]-6}, {t,0,2þ}, ViewPoint Æ {1,.0.5,8},
DisplayFunction Æ Identity]

-Graphics3D-

Show[mb1, ps1, DisplayFunction:>$DisplayFunction]

-Graphics3D-

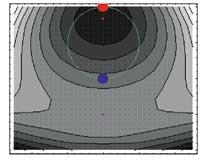
kp2=ContourPlot[g[x,y], {x,-2.5,2.5}, {y,-3,1},
AspectRatio Æ Automatic,
DisplayFunction Æ Identity]

-ContourGraphics-

mb2=ParametricPlot[{Cos[t], Sin[t]}, {t,0,2 þ},
PlotStyle Æ RGBColor[0,1,0],

AspectRatio Æ Automatic,
DisplayFunction Æ Identity]

-Graphics-

ps2=Graphics[{{RGBColor[1,0,0], PointSize[0.06], Point[{0,1}]}, {RGBColor[0,0,1], PointSize[0.06], Point[{0,-1}]}}]

-Graphics-

mut2=Graphics[{{RGBColor[0.5,0,0.5],
Polygon[{{-0.025,-2.025},{-0.025,-1.975},
{0.025,-1.975},{0.025,-2.025},
{-0.025,-2.025}}]},{RGBColor[1,0,0],
Polygon[{{-0.025,2/3-0.025}, {-0.025,2/3+0.025},{0.025,2/3+0.025},
{0.025,2/3-0.025}, {-0.025,2/3-0.025}}]}}]

-Graphics-

Show[kp2, mb2, mut2, ps2, DisplayFunction:>$DisplayFunction]

-Graphics-

• Iruzkinak

Lehendabizi, mutur arruntak kalkulatu ditugu ohizko metodoaren bidez. Hau da, D agindua erabiliz lehenengo deribatu partzialak kalkulatu ditugu eta zerorekin berdinduz sortzen den ekuazio-sistema ebatzi Solve-ren bidez. Union agindua erabili dugu sistemaren soluzio errepikatuak ezabatzeko. Azkenik, bigarren deribatu partzialekin hessearren segida osatu dugu eta puntu bakoitzari dagokion segidaren arabera, muturrak nolakoak diren erabaki dugu. Plot3D, Graphics3D eta Show aginduekin egindako irudian bereiz daitezkeenak dira mutur horiek.

Bigarren atalean Lagrange-ren metodoa erabili dugu mutur baldintzatuak kalkulatzeko. Horretarako, D eta Solve aginduez baliatu gara lehen bezala. Gero, funtzioaren eta baldintzaren hiru dimentsioko irudiak egin ditugu, Plot3D eta ParametricPlot3D erabiliz. Beherago, funtzioa eta baldintzaren arteko ebakidura-kurba eta topatutako puntuak irudikatu ditugu Graphics3D, ParametricPlot3D, Point eta Show aginduekin.

Azkenik, funtzioaren eta baldintzaren goitiko proiekzioa egin dugu (ContourPlot) eta bertan, mutur arruntak (Polygon, karratua) eta baldintzatuak (Point, zirkulua) kokatu ditugu.