Mathematica (i IV)
4t Volum delimitat per les dues superfícies
- Enunciat
Calculem ara el volum que delimiten totes dues superfícies en l'espai. Per a això utilitzarem una doble integral. Per a definir els límits de les integrals, representarem les projeccions de superfícies des de diferents punts de vista.
- Passos de la resolució
Primer calcularem els extrems normals de la funció per a després poder comparar-los amb els extrems condicionats. Calcularem els extrems condicionats utilitzant el mètode de multiplicadors de Lagrange.
- Instruccions a utilitzar
- ParametricPlot3D: realitza un gràfic tridimensional a partir d'equacions paramètriques. S'utilitza per a representar superfícies que no poden expressar-se com a funcions.
- ViewPoint: mostra la imatge tridimensional des d'un punt de vista concret.
- DisplayFunction: permet visualitzar el gràfic o mantenir-lo ocult.
- Xou: mostrarà els components gràfics.
- Graphics: convertirà la dada que se li dóna en un element representable.
- Circle: amb centre i radi representa la circumferència.
- Disk: amb centre i radi representa el cercle.
- Rectangle: representa el rectangle amb els vèrtexs inferior esquerre i superior dret.
- RGBColor: color de la imatge d'un gràfic.
- Axes: característica de representar o no els eixos dels gràfics.
- AspecRatio: característica de representar la proporció entre els eixos del gràfic.
- ViewPoint: mostra la imatge tridimensional des d'un punt de vista concret.
- Integrate: calcula la integral. Mitjançant dues variables, calcula la integral doble.
- Simplify: simplifica una expressió algebraica.
%, fa referència al resultat anterior.
- Resolució per Mathematica
Equacions cartesianes:
esfera x2 + y2 + z2 = Cilindre 4: x2 + y2 - 2y = 0Equacions paramètriques:
esfera: | x = 2cos[t] cos[v], | cilindre: | x = 2sin[t] cos[t], |
| i = 2sin[t] cos[v], | i = 2sen[t]2, | ||
| z = 2sen[v], | z = z |
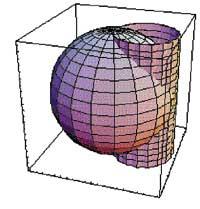
Imatge tridimensional:
e = ParametricPlot3D[{2cos[t]cos[v], 2sin[t]cos[v], 2sin[v]}, {t,0,2ler}, {v,-cer/2,ler/2}, View>{3,1,1.5}, DisplayFunction <Identity]
-Graphics3D-
z = ParametricPlot3D[ {2sin[t]cos[t],2sin[t]2,z}, {t,0,2{}, {z,-2,2}, ViewPoint Regla {3,1,1.5}, DisplayFunction> Identity]
-Graphics3D-
Xou[e, z, DisplayFunction: $DisplayFunction]
-Graphics3D-
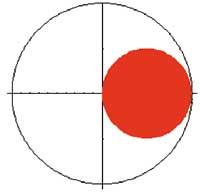
Projecció en planta:
pc=Graphics[{Circle[{0,0},2], {RGBColor[1,0,0], Disk[{1,0},1]}, Axes> True, AspectRatio Automatic]
-Graphics3D-
Xou[xliff-newline]
-Graphics3D-
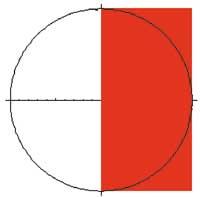
Projecció prèvia:
Abr=Graphics[{{RGBColor[1,0,0], Rectangle[{0,-2},{2,2}]}, Circle[{0,0},2]}, Axes- True, AspectRatio-Automatic]
-Graphics3D-
Xou[abr]
-Graphics3D-
Projecció des de la dreta:
epr=Graphics[{{RGBColor[1,0,0], Rectangle[{-1,-2},{1,2}]}, Circle[{0,0},2]}, Axes> True, AspectRatio Regla Automatic]
-Graphics3D-
Xou[epr, Axes> True]
-Graphics3D-
Integral doble:
Límits d'integrals en coordenades cartesianes:
i Prudencio [0, 2],x Convé [-] (2 i - y2), » (2 i - y2)]integrat: z = » (4 - x2 - y2).Límits d'integrals en coordenades cilíndriques:
integrant
z = r * (4 - r2)Nota: amb aquests límits només calcularem la meitat superior del volum.
Integrate[r*Sqrt[4-r2],{t,0,{},{r,0,2sin[t]}]?8/3
+ 4/9 (-4 + 3ess) - 4/9 (4 + 3?)
Simplify[%]
8/9 (-4 + 3ler)
Això és la meitat superior del volum. Per tant, el volum total:
2 * 16/9
(-4 + 3ash)
- Comentaris
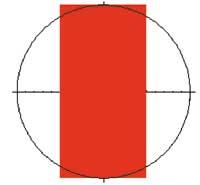
Primer hem fet una imatge tridimensional per a captar la idea de volum. Per a això hem utilitzat les tradicionals ordres ParametricPlot3D i Xou i hem triat l'enfocament estàndard a través de la característica ViewPoint. A continuació, hem representat les tres projeccions de volum, la superior, la frontal i la dreta, utilitzant les ordres Disk, Rectangle, Circle, Graphics i Xou. En ella també hem aprofitat DisplayFunction, RGBColor, AspectRatio i Axes. Finalment, hem calculat la integral doble amb l'ordre Integrate i simplifiquem el resultat mitjançant Simplify. D'aquesta forma hem aconseguit la meitat del volum. El volum total s'obté multiplicant el resultat anterior (%) per dos.
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian











