Quatre ou cinq couleurs

1993/01/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Combien de couleurs faut-il pour peindre une carte pour que deux régions voisines soient de couleurs différentes ?

Faire des cartes à quatre couleurs n'est pas très difficile. Il peut être démontré qu'il est suffisant avec cinq couleurs pour toutes les cartes. Mais est-il suffisant et nécessaire d'utiliser quatre couleurs?, à savoir, pourriez-vous faire une carte de cinq couleurs?

Bien qu'il ait été indiqué que les premiers à utiliser quatre couleurs étaient cartographes, il semble que le premier à expliquer la conjecture était l'élève de Francis Guthrie Edinburgh. Il a commenté son frère, le chimiste Frederick, qui l'a fait savoir à son professeur de mathématiques Augustus Morgan en 1852. La conjecture est devenue célèbre lorsque le grand mathématicien Arthur Cayley reconnu qu'en 1878 le sujet avait été inutile. De nombreuses preuves du théorème furent ensuite exposées. Bientôt, vous remarquerez que tout le monde avait une erreur.

N. Wiener, créateur de la cybermatique, a admis que dans l'autobiographie “Ex-Prodigy” a rencontré le problème (comme tous les mathématiciens) et il a échoué. La situation actuelle du problème (que nous savons) est la suivante: Il a été vérifié pour être respecté sur toutes les cartes qui n'ont pas plus de 38 limites. Le résultat est faible. Cependant, étant donné qu'il ya plus de 1038 cartes différentes, il semble que ce n'est pas si mauvais. Les ordinateurs actuels ne peuvent pas non plus analyser toutes les configurations au bon moment.

Si le problème est attrayant et fascinant, c'est parce qu'il semble facile à démontrer. L'absence de tests est actuellement irritant, étant donné que théorèmes similaires ont été montrés pour des surfaces plus complexes. Par exemple, sur des surfaces unilatérales, le ruban de Möbius, la bouteille de Klein et le plan projectif, il a été démontré que le nombre de couleurs suffisant et nécessaire est de 6. À Torua ce chiffre est de 7. (La sphère est équivalente dans ce problème au plan).

Pour comprendre la difficulté du problème, nous allons vous présenter un jeu. Deux joueurs ou plus peuvent participer. Le but est de trouver une carte qui nécessite cinq couleurs.

Le premier joueur représentera une région.

Le second peignera la région précédente et représentera une autre

Le suivant peint la dernière région et représente une autre (avec une limite avec l'une des régions précédentes).

Il faut continuer ainsi jusqu'à ce qu'un joueur ait besoin de la cinquième couleur.

Pour continuer à approfondir le problème, voici trois autres exercices.

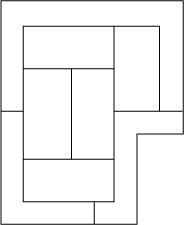
Combien de couleurs faut-il pour peindre la figure 1 pour que les deux régions avec une limite commune n'aient pas la même couleur?

Supposons que vous voulez peindre la figure 2 avec 4 couleurs. Il s'agit de peindre chaque région d'une couleur et deux zones contiguës de couleur différente. La zone supérieure a une superficie de 16 dm2 et le reste de 8 dm2. La peinture est aussi rouge que pour remplir 24 dm2, le jaune est aussi rouge que le rouge, le vert 16 dm2 et le bleu est lent pour atteindre 8 dm2. Comment faire ?

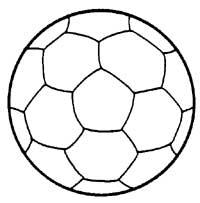
Sur le ballon de football il y a 32 régions: 20 hexagonales et 12 pentagonales. Combien de couleurs sont nécessaires pour peindre les 32 régions, pour éviter que deux régions de la même couleur aient des limites communes ? Quatre doit être suffisant. Essayez sur le ballon et non sur l'image.

Une fois les “exercices” précédents effectués, nous croyons que vous serez en mesure de comprendre l’essence du problème. Malheureusement il est difficile de prouver que cinq couleurs sont suffisantes pour n'importe quelle carte lisse. Cependant, la démonstration du théorème à deux couleurs peut être incluse dans cet article.

Considérons toutes les cartes plates qui peuvent être construites en utilisant des lignes droites (comme le damier). 4a. si vous prenez la carte de l'image, il ne sera pas difficile de prouver que vous avez seulement besoin de deux couleurs à peindre. Si on ajoute une droite à n'importe quelle carte formée de droites (droite noire de l'image), la nouvelle droite divise la carte en deux parties. Chacun de son côté serait bien peint, mais des deux côtés de la droite il ya des régions de la même couleur. Pour obtenir une situation optimale, il suffirait d'échanger des couleurs sur la carte d'un côté de la droite (4b. Image).

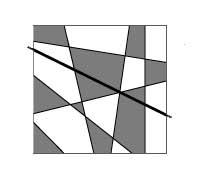
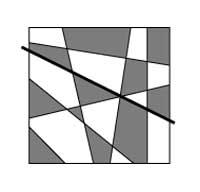
Si nous dessinons une autre droite, nous devrions faire la même chose, c'est-à-dire que nous échangerons les couleurs de la carte d'un côté de la droite. Le raisonnement peut être appliqué à n'importe quel nombre de droites et ainsi, par induction mathématique, il est prouvé qu'ils sont deux couleurs suffisantes pour peindre toutes les cartes qui peuvent être obtenues directement.

La démonstration peut être étendue à des cartes formées par des lignes ouvertes et indéfinies et des courbes fermées sans spirale (Figure 5). Si une ligne traverse la carte, les couleurs des régions situées de côté doivent changer. Si la courbe est fermée, les couleurs des régions intérieures (ou extérieures) changeront. Des courbes spirales peuvent également être introduites, mais la procédure de surchauffe est difficile.

Il faut noter que dans ce type de cartes tous les sommets sont paires, c'est-à-dire que deux lignes sont croisées. On peut démontrer que la condition suffisante et nécessaire pour pouvoir peindre une carte avec deux couleurs est que tous les sommets soient paires.

Enfin, en mode exercice, prenez une carte non peinte et essayez de peindre avec le moins de couleurs possible.