Laberints

1993/09/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Res més llegir la paraula Laberint, ens ve al capdavant la història del laberint de Creta. Aquesta història ens conta que una vegada la reina Pasifae es va enamorar d'un toro blanc. Per a poder acostar-se a ell, va manar a Dèdal construir una vaca vaca vaca. Amb aquest truc va poder acostar-se al toro i (no sabem com, perquè com sempre se'ns amaga la part de les històries) d'aquella relació va sorgir Minotaure. Sorprès i avergonyit, el rei Minos va ordenar a Dèdal que ocultés a Minotaure. Dèdal va construir un ampli laberint al qual van entrar Minotaure. La història no acaba aquí, però el nostre tema no és la vida de Minotaure, sinó el laberint.

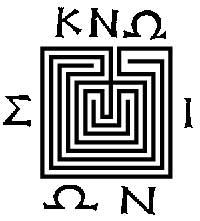
D'aquesta història han quedat monedes de bronze i plata, a pesar que els grecs van pertànyer a l'illa. A un costat es pot veure la cara d'un Minotaure o déu. A l'altre costat hi ha un laberint.

No obstant això, el de Creta no és el primer laberint conegut. De fet, l'historiador grec Heròdot parla d'un laberint egipci, dos estayas i una enorme extensió. El mateix herodoto va estar en el superior i només podien entrar els iniciats en l'inferior.

Al llarg dels segles els laberints van quedar oblidats fins que en l'Edat mitjana la llosa de les catedrals es va transformar en sendera. A vegades les imatges es repeteixen en els murs. Alhora se'ls dóna nous noms, com a meandre, dèdal, camí de Jerusalem, ... Aquest últim es considerava substitut dels camins rals a les Croades. A Anglaterra es construïen amb tanques i cèrcols verds. En Hampton Court hi ha un laberint encara visible. També els construïts en pedra a Escandinàvia.

XX. En el segle XX han aparegut en diferents mitjans. Els científics analitzen el comportament dels animals en el laberint. S'ha creat una escola de psicologia als EUA, els postulats dels quals s'han aplicat en la guerra del Viet Nam. Altres científics investiguen la marxa d'un autòmat. Quan l'autòmat arriba a un cantó, sempre gira a la mateixa cara. Abans de tarda, serà capaç d'anar pel camí més curt a qualsevol lloc. Si l'autòmat opta pel gir aleatori, no sabríem si encertaria o no. Està realitzant les primeres sessions d'intel·ligència artificial.

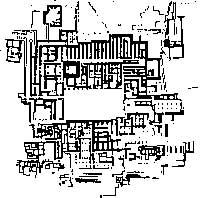
Ara sabem que es pot programar per a ficar i treure moltes màquines del laberint, però què va fer Teseu per a trobar a Minotaure? El fil que li va donar Ariadna li assegurava el retorn. No així el camí cap al Minotauror. Plutarko, la font més completa, diu que Ariadna li va ensenyar el camí, però no diu com. Però l'arqueologia ens dóna una altra interpretació. Sir Arthur Evans va descobrir l'antiga capital de Creta, Knosos, l'antic palau real. En els murs es podia veure la imatge de la moneda i les figures taurines. En alguns llocs es veia una destral doble anomenada labrys. Laberint, per tant, seria el lloc dels labrys. Minos era el nom general del governador (com César o Tsar) i els minotaures els toros del rei. Per tant, Minotaure i el seu habitatge estaven al capdavant dels visitants del palau, per la sorpresa que els causava la grandesa del palau. Va ser el constructor del palau Dèdal (Figura 2).

Per descomptat, si no hi havia laberint tampoc es necessitaven instruccions. En la imatge de la moneda ningú pot perdre's perquè el camí és únic. Els laberints reals no van estar fins al final de l'Edat mitjana. Hampton Court i Hatfield House necessiten un pla o instruccions per a arribar fins al centre. L'ideal seria l'algorisme o aclariments que es poden utilitzar en tots els casos, ja que el pla d'un laberint no serveix per a un altre.

Entre els laberints caldria diferenciar dos tipus: els que tenen recorreguts tancats, és a dir, els laberints amb un tros de barrera separat de la resta (d'unió múltiple) i els altres (d'unió simple). Les instruccions per a caminar en el laberint d'unió simple són senzilles. Posa la mà en una paret i comença a caminar sense llevar-la. Aquest mètode assegura l'entrada i sortida encara que no sigui el camí més curt.

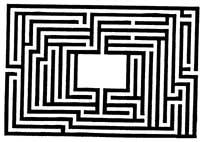
Per a moure's pels laberints multi-enllaç es requereix un altre algorisme. Aquest algorisme va ser emès el segle passat pel senyor Tremaux. Agafa el llapis i comença a dibuixar sense llevar-te la paret com abans. Com abans, cal donar la volta en els camins tancats per una paret que no està ratllada. En algun encreuament veuràs el camí traçat. Retrocedeixi per la paret no ratllada. Si no hi ha aquest tipus de parets, agafa un altre camí amb una línia. No accedeixi mai als camins amb totes dues parets traçades. Si en arribar al centre deixes de dibuixar, a la sortida et conduiran camins amb una sola línia.

Els citats laberints, excepte el d'Egipte, són bidimensionals, és a dir, estan situats sobre un pla. La tercera dimensió s'obté mitjançant la superposició de diversos laberints de la mateixa planta i la unió dels moments corresponents. Una altra opció és que els camins que van de dalt cap avall i de baix cap amunt també formen laberints. No obstant això, el mateix algorisme donat en tots els casos serveix per a poder entrar i sortir.