Rincón del lector. Octubre

1988/10/01 Agirregabiria, Juan M. Iturria: Elhuyar aldizkaria

• Fisika

Pregunta: Segons la teoria de la Relativitat General d'Einstein, la Gravetat és la curvatura espacial de l'espai/temps al voltant de cada massa. Per això l'Univers seria de 4 dimensions, però no totes són espacials, una és el temps. Però Martín Gardner en el seu llibre "Esquerra i dreta en el Cosmos" diu: Segons la teoria d'Einstein, si un astronauta viatja el més directament possible, arribaria al seu punt de partida després de recórrer una distància suficient: el món tridimensional es considera la hipersuperficie d'una hiperesfera de 4. La pregunta és: Com es dedueix això? És conseqüència del que s'ha dit anteriorment o d'una altra manera de dir el mateix? No és el mateix la curvatura local (creada per masses) que la de tot l'Univers. D'altra banda, aquestes 4 dimensions són espacials en aquest cas? (en cas afirmatiu, no és l'únic que proposa aquest Einstein, com crec).

Agustín Mendizabal

Resposta: Si veig alguns aspectes en la carta del lector, intentaré aclarir-los un a un.

1.- Segons el lector, en la Relativitat General cada massa (cada estrella, per exemple) crea una curvatura local al seu voltant. Però en Cosmologia cal tenir en compte la massa de tot l'Univers. De fet, en l'escala cosmològica (és a dir, en l'escala de tot l'Univers), en tots els llocs existeix una distribució mitjana de masses i, per tant, una curvatura mitjana no nul·la. D'aquesta forma, la curvatura local generada per cada estrella es produeix microscòpica des del punt de vista cosmològic global i s'analitza únicament la curvatura mitjana global generada per totes les masses. El mateix ocorre en tots els àmbits de la física: malgrat ser una teoria local fonamental, es produeixen efectes globals com a conseqüència de la suma dels efectes locals.

2.- Tenint en compte les equacions fonamentals de la teoria d'Einstein i algunes hipòtesis senzilles com l'homogeneïtat de l'espai i la isotropia, s'obté el model més simple de l'Univers. Igual que ocorre amb tots els models de la Física, aquesta tampoc serà definitiva ni final. Però sembla que dins dels seus límits és una aproximació precisa, útil i productiva. Conegut com Robertson-Walker, és el nucli del model standard. En teoria, la geometria d'aquest model pot ser de tres tipus diferents, i en un d'ells pot ocórrer el que el lector esmenta: ...si un astronauta va el més correctament possible, arribaria al seu punt de partida... Aquí volem subratllar que es tracta d'una possible conclusió teòrica (però no necessàriament).

3.- D'altra banda , el lector no està equivocat. En la Relativitat General només hi ha tres dimensions espacials.

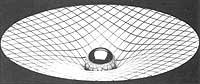
4.- Però fem algunes consideracions matemàtiques. Perquè considerem l'espai tridimensional en el model esmentat com un hiperespai de quatre dimensions (i com uneixi hipersuperficie esfèrica) des del punt de vista matemàtic (insistirem). Però hi ha una altra possibilitat equivalent: pensar que està en si (i no en cap altre espai). Per a explicar-ho millor, prenguem com a exemple un pla. És possible assumir-ho o pensar que està dins de l'espai (o en un hiperespai amb quatre, cinc, ..., dimensions il·limitades). En qualsevol cas només té dues dimensions. El pla té caràcter propi i no depèn de la seva ubicació dins d'un altre espai. El mateix ocorre amb una superfície esfèrica.

A l'escola estudiem la definició de la superfície esfèrica dins de l'espai, però com van demostrar Gauss i Riemann en el segle passat, la definició de la mateixa superfície esfèrica pot fer-se sense cap altre espai i mitjançant dues dimensions. Totes dues definicions són totalment equivalents i en ambdues la mateixa superfície només té dues dimensions. De la mateixa manera, l'espai de l'Univers de Robertson-Walker (al marge del temps) només té tres dimensions, si bé és possible (però en cap cas necessari) pensar que està dins d'un altre hiperespai.

5.- Des del punt de vista físic aquest hiperespai imaginari és possible, però totalment inútil, ja que la hipòtesi de la seva existència no té cap efecte ni manera de demostrar-lo. La imatge de l'espai com hipersuperficie esfèrica d'un hiperespai pot ser a vegades útil per a comprendre millor algunes propietats, però no és en absolut casual i a vegades pot resultar perjudicial (sembla que ha estat així en el cas del lector). És cert que entendre aquest tipus d'espais corbs sense l'ajuda d'un altre espai pla no és gens fàcil, perquè el nostre sentit comú és molt limitat. Tal vegada no puguem entendre de debò aquest tipus de coses (segurament l'estudi d'aquesta possibilitat seria un problema profund de la psicologia), però és possible adquirir el costum d'utilitzar aquest tipus de conceptes i, al final, pensem que els hem entès.

6.- Per a finalitzar, una nota. A diferència de la Relativitat General, en algunes teories actuals les dimensions són més de quatre. Però això és una altra cosa, perquè la resta de dimensions no són el que habitualment diem espai o temps.

Juan Mª Agirregabiria
Universitat del País Basc
Universitat Basca d'Estiu