Harrijasotzearen fisika

Gaur egun “Euskal Joko eta Kiroletako Euskal Federazioak” indarrean duen arautegiak, ongi definitzen du “harrijasotzea”. Hain zuzen lehen hiru artikuluetan harria zer den definitzen du: harri hutsa izan behar du (harkaitz edo harrobi berberekoa), harriari arrotz zaion inolako gairik erantsi gabea, harrobi berbereko bi harri edo gehiago elkarri eransterik ez da onartzen, harriari pusketaren bat askatzen bazaio pisu espezifiko bereko pusketa kolaz erantsi behar zaio eta arraildura duelako harginak ziriak ipintzen badizkio, guztira zirien pisuak ezin du 500 gramo baino handiagoa izan.

Harrijasotzea

Ikus dezagun arautegiak harrientzat zein forma eta ezaugarri arautu dituen. Harrijasotzeko sei harri-mota onartzen ditu arautegiak (ikus 4. artikulua) eta ondoko hauek dira: kuboa, esferikoa, usadio zaharreko zilindroa, usadio zaharreko laukizuzenduna, gaurko usadioko zilindroa eta gaurko usadioko laukizuzenduna. Araututako harri hauez gain gaur egun beste harri irregular batzuekin ere saioak egiten dira noizbehinka (Amezketako Albizuriko harri irregularrarekin, adibidez).

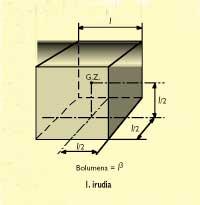
Kuboa

Harri-mota hau hexaedro-erakoa da, bere sei aldeak karratuak eta berdinak ditu eta ez dauka eskuzulorik. Harri honen grabitate-zentrua kuboaren zentru geometrikoan dago. "Harri kubikoa" koadroan, material desberdinez egindako gorputz kubikoen neurriak (l aldearen luzera) eta pisuak ematen dira.

Esfera

Harri esferikoa, bola bat da, noski. Ez dauka heldulekurik. Harri honen grabitate-zentrua esferaren zentru geometrikoan dago.

Goiko koadroan material desberdinez egindako gorputz esferikoen neurriak (d diametroaren luzera) eta pisuak ematen dira.

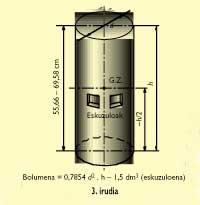
Usadio zaharreko zilindroa

Harrizko zilindroa da. Eskuzulo edo heldulekuak harrian bertan landuak dauzka, baina eskuzulo horiek ezin dira guztira 1,5 dezimetro kubiko edo litro baino handiagoak egin (ikus arautegiko 4.f. artikulua). Harriaren altuerak berriz, 55,66-69,58 zentimetro bitartekoa (24-30 ontza bitartekoa) izan behar du (ikus arautegiko 5. artikulua). Harri honen grabitate-zentrua zilindroaren zentru geometrikotik oso gertu dagoela esan daiteke. Eskuzulorik ez balu, zentru geometrikoan bertan egongo litzateke, baina eskuzuloak medio, milimetro bat edo beste desplazatua du grabitate-zentrua. Ardatzetik kanpoko aldera dago zertxobait.

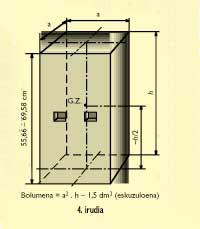
Usadio zaharreko laukizuzenduna

Harri honen alboko lau aldeak laukizuzenak dira. Ipurdia eta goiko aldea berriz, karratuak ditu. Eskuzulo edo heldulekuak harrian bertan landuak dauzka, baina eskuzulo horiek ezin dira guztira 1,5 dezimetro kubiko edo litro baino handiagoak egin (ikus arautegiko 4.d. artikulua). Harriaren altuerak berriz, 55,66-69,58 zentimetro bitartekoa (24-30 ontza bitartekoa) izan behar du (ikus arautegiko 5. artikulua). Harri honen grabitate-zentrua, oinarri karratuko prisma honen zentru geometrikotik oso gertu dagoela esan daiteke. Eskuzulorik ez balu, zentru geometrikoan bertan egongo litzateke, baina eskuzuloak medio, milimetro bat edo beste desplazatua du grabitate-zentrua. Ardatzetik kanpoko aldera dago zertxobait.

Oraingo usadioko zilindroa

Usadio zaharreko zilindroarekin dituen diferentziak ondoko hauek dira: eskuzuloak nahi bezain handiak izan ditzake eta harriaren edozein lekutan arindu daiteke pisua, baldin eta ipurdiaren zirkunferentzia eta goiko zirkunferentzia ukitu gabe uzten badira (ikus arautegiko 4.g. araua). Harriaren altuerak berriz, 55,66-69,58 zentimetro bitartekoa (24- 30 ontza bitartekoa) izan behar du (ikus arautegiko 5. artikulua).

Harri honen grabitate-zentrua zilindroaren zentru geometrikotik oso aparte dagoela esan daiteke, harriaren azpialdean pisua asko arindu zaiolako. Grabitate-zentrua, zilindroaren zentru geometrikoa baino dezentez gorago dago.

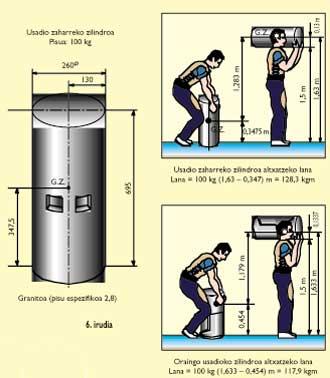
Ondoko 5. irudian, oraingo usadioko granitozko 8 arroa edo 100 kiloko zilindroa erakusten da (guk neurtu ahal izan dugun bat). Hiru bista eta perspektiba (behean eskuinean) erakusten dira. Bertan harriaren forma, neurriak eta grabitate-zentrua (G.Z.) non dagoen erakusten da. Irudi geometriko berezia delako problema erraza ez den arren, harri honen grabitate-zentrua kalkulatu dugu. Horretarako harria zati desberdinetan banatu dugu eta gero zati horiek b. irudian bezala kontsideratu eta formulak aplikatu ditugu.

5. irudian bertan ikusten da grabitate-zentrua (G.Z.) eta usadio zaharreko zilindroa balitz baino 107 milimetro gorago du. Horrez gain, harriaren grabitate-zentrua (G.Z.) zilindroaren ardatzetik 31,3 milimetro desplazatua dago. Harrijasotzaileak harria gerrian jiratu eta bularrean gora altxatzen ari denean, pisua 31,3 milimetro bularralderago edukitzea mesederako du.

6. irudian (ezkerrean) granitozko 100 kiloko usadio zaharreko zilindroaren neurriak eta grabitate-zentruaren kokaera ipini ditugu. Gero irudian (eskuinean) eskema batean sorbaldaraino 1,5 metroko altuera duen harrijasotzaile batek usadio zaharreko zilindroa (goian) jasotzeko egiten duen lana kalkulatu da. Horren azpian, harrijasotzaile berak oraingo usadioko 100 kiloko harria altxatzen egiten duen lana kalkulatzen da. Usadio zaharrekoa altxatzeko 128,3 kilogrametroko lana egin behar du, eta oraingo usadiokoa altxatzeko 117,9 kilogrametrokoa. Portzentaiatan emanda, % 8 gutxiago da oraingo usadiokoa altxatzeko lana. Beraz, teorikoki % 8 errazagoa da kasu jakin honetan harri berria altxatzea.

Oraingo usadioko laukizuzenduna

Usadio zaharreko laukizuzendunarekin dituen diferentziak ondoko hauek dira: eskuzuloak nahi bezain handiak izan ditzake eta harriaren edozein lekutan arindu daiteke pisua, baldin eta ipurdiko karratuaren ertzak eta goiko karratuaren ertzak ukitu gabe uzten badira (ikus arautegiko 4.e. araua). Harriaren altuerak berriz, 55,66-69,58 zentimetro bitartekoa (24-30 ontza bitartekoa) izan behar du (ikus arautegiko 5. artikulua).

Harri honen grabitate-zentrua prismaren zentru geometrikotik dezente aparte dagoela esan daiteke, harriaren azpialdean pisua asko arindu zaiolako. Grabitate-zentrua, oinarri karratuko zentru geometrikoa baino dezentez gorago dago.

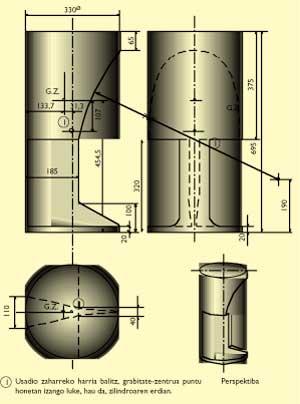
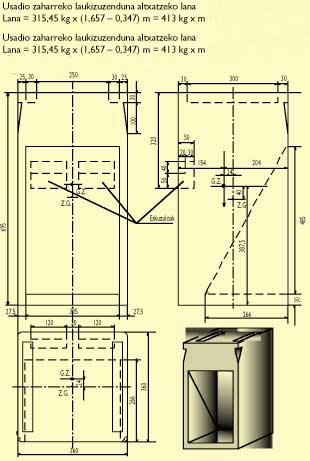
7. irudian, oraingo usadioko laukizuzenduna erakusten da. Baritinazko baten neurriak ipini ditugu. Harriak (berunik eta ezer erantsi gabe) 315,45 kilo pisatzen dituela kalkulatu dugu.

Esan dezagun baritina mineral zuri edo kolore gabekoa dela. Bario sulfato (Ba SO4) izeneko konposatu kimikoa da eta astuna ere bai. 4 eta 4,7 bitarteko pisu espezifiko erlatiboa izaten du. Gure harrijasotzaile famatuenek marka handiak egiten dituztenean baritinazko harria erabiltzen dute.

Harriaren hiru bista eta perspektiba ematen dira. Harriaren forma, neurriak eta grabitate zentrua non dagoen ikus daiteke.

Guk harri honen grabitate-zentrua kalkulatu dugu. Horretarako harria zati desberdinetan banatu dugu eta gero zati horiek b. irudian bezala kontsideratuz formulak aplikatu ditugu. 7. irudian bertan ikusten da grabitate-zentrua (G.Z.) eta usadio zaharreko laukizuzenduna balitz baino 40 milimetro gorago du; zentru geometrikoa (Z.G.) baino gorago, alegia. Horrez gain, harriaren grabitate-zentrua (G.Z.) paralelepipedo edo prisma karratuaren ardatzetik 24 milimetro desplazatua dago. Harrijasotzaileak harria gerrian jiratu eta bularrean gora altxatzen ari denean, pisua 24 milimetro bularralderago edukitzea mesederako du.

Lurretik sorbaldaraino 1,5 metroko altuera duen harrijasotzaile batek, baritinazko 315,45 kiloko usadio zaharreko laukizuzenduna jasotzeko egiten duen lana kalkulatu da. Harrijasotzaile berak oraingo usadioko 315,45 kiloko harria altxatzen egiten duen lana ere kalkulatu da.

Usadio zaharrekoa altxatzeko 413 kilogrametroko lana egin behar du, eta oraingo usadiokoa altxatzeko 399,5 kilogrametrokoa. Portzentaiatan emanda, % 3,3 gutxiago da oraingo usadiokoa altxatzeko lana. Beraz, teorikoki % 3,3 errazagoa da kasu jakin honetan harri berria altxatzea.

5. irudia. Oraingo usadioko zilindroa. Pisua 8 arroa edo 100 kilo. Granitozkoa.

Pisujasotzea

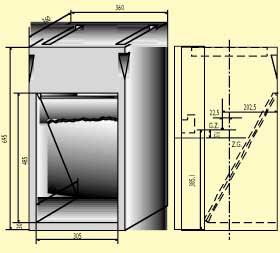
Guk 322 kiloko pisu baten grabitate-zentrua kalkulatu egin dugu eta 8. irudian bertan adierazi ditugu G.Z. horren distantziak. Argitu beharra dago kalkuluak egiteko elementu guztiak zehatz-mehatz ez ditugula hartu (pinturaren pisua, adibidez, ez dugu kontsideratu) eta grabitate-zentruaren distantzietan milimetroren bateko okerra egon daitekeela.

Guk harri honen grabitate-zentrua (G.Z.) kalkulatu dugu. Horretarako harria zati desberdinetan banatu dugu eta gero zati horiek b. irudian bezala kontsideratu ditugu eta formulak aplikatu dizkiogu. 8. irudian bertan ikusten da G.Z., eta usadio zaharreko laukizuzenduna balitz baino 37,6 milimetro gorago du; zentru geometrikoa (Z.G.) baino gorago, alegia. Horrez gain, harriaren grabitate-zentrua (G.Z.) paralelepipedo edo oinarri karratuko prismaren ardatzetik 22,5 milimetro desplazatua dago. Harrijasotzaileak harria gerrian jiratu eta bularrean gora altxatzen ari denean, pisua 22,5 milimetro bularralderago edukitzea mesederako du. Gerrialdean jiratu arte ordea, 22,5 milimetroko desplazamendua kalterako du, ondoko irudietan erakutsiko denez.

Dena dela, grabitate-zentrua orain arte ikusi ditugun harri eta pisuetan simetri planoan dago, hau da, harri simetrikoak aztertu ditugu. Harrijasotzaileak harria sorbaldan goian horizontal duenean, grabitate-zentrutik buru aldera pisuak 180 milimetro ditu eta kanpoko aldera ere 180 milimetro (berdin, alegia). Gerta liteke harrijasotzaileak pisuaren grabitate-zentrua buru alderago eduki nahi izatea (pisuak beste aldera ihes egiten diolako edo). Kasu horretan grabitate zentruak ez luke erdian egon behar; buru alderago baizik.

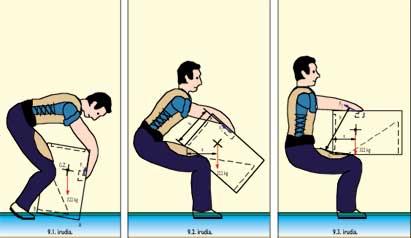
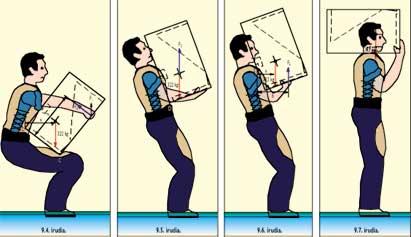
Orain, harri jasotzean altxaldi bat egiteko 322 kiloko pisuak eta eragindako goranzko indarrak nolakoak izaten diren labur aipatuko dugu, 9. irudian erakusten diren zazpi posturak aztertuz.

9.1. posizioan, pisua zerbait aurrera okertuta dago. Horregatik ipurdiko A puntua lurra ukituz dago eta B puntua airean. Grabitate-zentruan 322 kiloko pisua dago behera bertikalki eragiten. Pisuak berak eta kirolariak gorantz eragiten dion F ₁ indarrak, harri laukizuzenduna atzeraka birarazten dute, harik eta B puntuak lurra ukitu arte. F ₁ indarra oso txikia da hasieran. B puntuak lurra ukitzen duenean gehiago biratzen segi dezan, indarra handiagoa da eta gure kalkuluen arabera 100 kilo ingurukoa izatera hel daiteke harriak lurra utzita aireratzen den arte.

9.2. Harriak lurra ukitzeari uzten dionean, kirolariak bere gorputzari atzera eragiten dio. Izan ere, batetik 322 kiloko pisua dago eta bestetik kirolariaren gorputzaren pisua (115 kilokoa edo). Harriak lurra ukitzeari utzi ondoren, pisuaren eta kirolariaren gorputzaren arteko grabitate-zentruak oinen parean egon behar du beti. Bien arteko grabitate-zentrua oina baino aurrerago balego, harria eta bera aurrera eroriko lirateke, eta oina baino atzerago balego, harria harrijasotzaileari gorputz gainera eroriko litzaioke.

Posizio honetan kirolariak harriaren goiko aldean ertzetan dituen bi koskak izterrean iltzatuak ditu eta puntu horiek izango dira eragiten diren indarren palanka-jokoan euste puntua. Posizio honetan harriari erori gabe eusteko, F ₂ = 293 kiloko indarra eragin beharko lioke gora harrijasotzaileak. Momentu horretan izan ere, 322 x a = F ₂ x b bete behar da. Hori eskatzen du palanken legeak. Indar hori harria bere horretan geldirik mantentzeko eragin behar da, baina beheragotik abiadura batez datorrenez, beharbada puntu horretan eragindako F ₂ indarra zerbait txikiagoa izango da.

Eukal Herriak berezkoa duen kiroletako bat harrijasotzea da. Gure kirolariak, marka "harrigarriak" hausten ari dira azkenaldian. Irudian 320 kiloko harriarekin egindako azken ikusten da.

9.3 posizioan, harria horizontal dago. 322 kilo bertikal behera tiratzen ari dira eta harrijasotzaileak F ₃ indarra egiten du gora, harria C puntuaren inguruan gerriraino jiratzeko. F ₃ indarra ez da horizontal egin behar; gora aldera baizik, palankaren b besoa ahalik eta handiena eta F ₃ indarra ahalik eta txikiena izan dadin. Posizio horretan izan ere, honakoa betetzen da: 322 x a = F ₃ x b . Gure kalkuluen arabera F ₃ 195 kilo ingurukoa da.

9.4. posiziora etortzeko, C puntuan harria jiratuta bi oinak (lehenengo bat eta gero bestea) erdira ekartzen ditu. Izan ere hasieran harria bi belaunen artean zuen eta orain belaunen gainean ditu. Gero esku bat eskuzulotik atera eta harriari atzetik heltzen dio eta ondoren beste eskuarekin gauza bera egiten du. Bi eskuekin atzetik helduta jiratzen hasten denean, C puntua ez eta D puntua (gerrikoan dagoen harriaren ertza) da palankaren euste-puntua. Kasu honetan ideala harriari bi eskuez irudiko F _i indarraren norabidean tiratzea litzateke, baina gorputzean besoek duten kokapenagatik eta formagatik irudian erakusten den norabidean F ₄ indarra eragiten da. Oreka mantentzeko 322 x a = F ₄ x b bete behar da. Gure kalkuluen arabera F ₄ indarra 225 kilo ingurukoa da.

9.5. posizioan harria gerrian jiratuta dago eta harrijasotzaileak F ₅ indarra gora egin behar dio. Bi eskuez 322 kiloko pisuari eutsi egiten dio, baina belaunak pixka bat okertuta izterrekin eta gorputz guztiarekin harriari kolpe bat jotzen dio gora eta zerbait ezkerrera (gero goian berdintzen duenean burua libratzeko). Kolpe horretan 322 kiloko indarra baino handiagoa eragiten da, geldirik dagoen harriari gorantz azelerazioa ezartzen zaiolako. Beraz, F5 indarra 322 kilo baino handiagoa da.

9.6. posizioan harriari gorantz lehen bezalaxe beste kolpe bat (edo bi) jo di(zki)o eta ia bizkarrean du. Une horretan palankaren euste-puntua E puntuan dago eta ondokoa bete behar da: 322 x a = F ₆ x b . Eskuez harriari azpitik helduta gora eragin behar dio F ₆ indarra. Gure kalkuluen arabera, indar hori 170 kilo ingurukoa da. 9.7. posizioan pisua bizkar gainean berdinduta erakusten da. Harrijasotzaileak postura horretan 322 kilo horiei eutsi besterik ez dio egiten.

7. irudia. Oraingo usadioko laukizuzenduna. Pisua 315,45 kilo. Baritinazkoa. Pisu espezifikoa 4,57.

Irudi-segida honetan garbi ikusten da altxaldian zehar gora eragin behar den indarrak zer-nolako eboluzioa duen. Lurra ukitzeari uzten dionean, hau da, 9.2. posizioan indar handia eragin behar da, eta 9.4. posizioan gerrian jiratzean ere bai. Gero 9.5 eta 9.6 posizioan harria bularrean denean ere une latzak pasatzen ditu kirolariak. Bi alderdi horiek bereiziko ditugu, beraz: a) gerrian jiratzea eta b) bularretik sorbaldara igotzea.

a) Gerrian jiratzea . Gerrian errazago jiratzeko, komeni da harria estua izateaz gain (hankak gehiegi zabaldu beharra ez izateko) grabitate-zentrua ahalik eta gorena edukitzea. 8. irudian erakusten den baritinak, bere grabitate zentrua lurretik 385,1 milimetrora du, hau da, zentru geometrikoa baino 37,6 milimetro gorago. Zenbat eta gorago egon, hainbat eta errazago jiratuko du gerrian. Bestetik, pisua lurretik altxatzen hasi eta gerrian jiratu arte grabitate-zentrua kirolaritik 202,5 milimetrora dago (ikus 8. irudia), hau da, zentru geometrikoa baino 22,5 milimetro urrutiago, eta hori kalterako du.

b) Bularretik sorbaldara igotzea. Bularretik sorbaldara igotzeko ordea, lehen mesederako zena orain kalterako da, eta alderantziz. Hasieran grabitate-zentrua zentru geometrikoa baino 37,6 milimetro gorago bazegoen, harria gerrian giratu ondoren zentru geometrikoa baino 37,6 milimetro beherago geratzen da, hau da, 9.5. posiziotik sorbaldan berdintzeraino tarte handiagoa du. Bigarren fase honetan, beraz, harriak hasieran (lurrean dagoenean) grabitate-zentrua zentru geometrikotik behera edukitzea komeniko litzateke. Harrijasotzaile bakoitzak ikusi behar du non ibiltzen den gaizkien (a) atalean ala b) atalean) eta horren arabera prestatu beharko du harri edo pisuaren grabitate-zentrua.

Gauza bera gertatzen da grabitate-zentruak harrijasotzailearen bularreraino duen distantziarekin. a) atalean zentru geometrikoa baino 22,5 milimetro urrunago zegoen (eta kalterako zen), baina orain gerrian jiratu ondoren bularretik hurbilago du (eta mesederako ere bai). Bistan da gerritik gora pisua zenbat eta bularralderago eduki hainbat eta errazago altxatuko duela bizkarrera. (Halterofilian ibiltzen direnek, adibidez, pisuaren grabitate-zentruan barran bularraren kontra-kontra edukitzen dute). Kasu honetan ere harrijasotzaileak aukera egin beharko du bere pisuaren grabitate-zentrua prestatzerakoan.

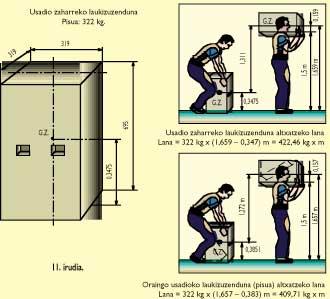
10. irudian baritinazko 322 kiloko usadio zaharreko laukizuzendunaren neurriak eta grabitate-zentruaren kokaera ipini ditugu. Gero irudian eskema batean lurretik sorbaldaraino 1,5 metroko altuera duen harrijasotzaile batek usadio zaharreko laukizuzenduna jasotzeko egiten duen lana kalkulatu da. Horren azpian, harrijasotzaile berak oraingo usadioko 322 kiloko pisua altxatzen egiten duen lana kalkulatzen da.

Usadio zaharrekoa altxatzeko 422,46 kilogrametroko lana egin behar du, eta oraingo usadioko pisua altxatzeko 409,71 kilogrametrokoa. Portzentaiatan emanda, % 3 gutxiago da oraingo usadiokoa altxatzeko lana. Beraz, teorikoki % 3 errazagoa da kasu jakin honetan usadio berriko pisua altxatzea. Portzentaia horrek begiratu batera txikia dirudi, baina tamaina honetako pisuetan kilolaurdena ere garrantzitsua da.

8. irudia. Oraingo usadioko laukizuzenduna. Pisua guztira. 322 kg.

Hala ere, gauza bat da bizkarrera altxatzeko egiten den lana eta pisu hori altxatzen erabili den potentzia (hau da, lana zati altxatzen erabilitako denbora; edo indarra bider distantzia zati denbora). Pisuaren grabitate-zentrua hasieran zenbat eta gorago egon, altxatzen egindako lana hainbat eta txikiagoa da eta altxaldi bat baino gehiago segidan egin behar direnean markak hausteko bidea grabitate-zentrua goian jartzea da, zalantzarik gabe.

Baina marka hausteko altxaldi bat bakarra egin behar denean (pisu handienetan hala izaten da), gerta liteke grabitate-zentrua hain goian jartzea kalterako izatea. Izan ere, orain arte markak hausteko saioan huts egin dutenean, gutxienez harria bularreraino igota eduki dute eta posizio horretan (9.5.ean) hasieran grabitate-zentrua goian jartzea kalterako da. Kasu horretan hobe litzateke hasieran grabitate-zentrua beherago ipini, gerrian jiratzen denbora gehiago igaro eta nekezago ibili, ahal balitz geratu eta deskantsatu (badakigu pisu horiek soinean direla deskantsu hartzea oso zaila dela), eta gero gerritik sorbaldaraino errazago igotzea.

Altxaldian denbora gehiago igarotzeak, potentzia txikiagoa erabiltzea esan nahi du. Potentzia, hasieran esana dugunez, indarra bider jasotako distantzia zati denbora da (Potentzia = F x d/t). Beraz, gerta liteke altxatzen denbora gehiago igarota batezbeste indar txikiagoa egin eta distantzia handiagoan pisua igotzea.

Eskerrak emanez

Lan hau bukatu aurretik, eskerrak eman nahi nizkieke Joan Mari Aranberri eta Ibon Aranberri osaba-ilobei beren laguntzagatik, eta bereziki Narziso Saralegiri, emandako argibide interesgarriengatik eta harriak ikusteko eta aztertzeko eskainitako erraztasunengatik. Federazioari ere bai, arautegia eman eta adeitsu hartu nautelako. Era berean, Euskal Kirol eta Jokoetan hain zintzo dabiltzan kirolari guztiak ere eskertu nahi genituzke.

Fisikako zenbait kontzeptu Harrijasotzaileen lana hobeto ulertzearren, lehenik eta behin interesgarria iruditzen zaigu hainbat kontzeptu Fisikaren ikuspegitik argitzea: Dentsitatea Dentsitatea, substantzia baten bolumen-unitateak duen “masa” da. Beraz, gorputzaren “masa” zati gorputzaren bolumena da dentsitatea. Bolumen-unitatetzat adibidez litroa (litroa = dezimetro kubikoa) hartzen badugu, litro horretako harriaren masa zati litroa (bolumena) izango litzateke harriaren dentsitatea. Dentsitate erlatiboa , erreferentzia gisa hartzen den gorputz baten dentsitatearekiko erlazioa da. Normalean erreferentzia gisa hartzen den gorputza ura izaten da. Pisu espezifikoa Substantzia baten bolumen-unitateak duen “pisua” da. Beraz, gorputzaren “pisua” zati gorputzaren bolumena da pisu espezifikoa. Bolumen-unitatetzat litroa hartzen badugu, litro horretako harriaren pisua zati litroa (bolumena) izango litzateke pisu espezifikoa. Kararrizko litro edo dezimetro kubiko batek 2,6 kilo “pisatzen” baditu, bere pisu espezifikoa 2,6 kg/1dm 3 -koa edo 2,6 kg/dm 3 -koa izango da. Pisu espezifiko erlatiboa , erreferentzia gisa hartzen den gorputz baten pisu espezifikoarekiko erlazioa da. Normalean erreferentzia gisa hartzen den gorputza ura izaten da. 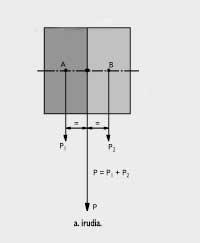Badakigu litro bat urek kilo bat pisatzen duela. Beraz, bere pisu espezifikoa 1kg/1dm 3 -koa da, hau da, 1kg/dm 3 -koa. Kararriak berriz, 2,6 kg/dm 3 -ko pisu espezifikoa duela esan dugu. Kararriaren pisu espezifiko erlatiboa, beraz, 2,6/1 (urarena) = 2,6 izango da. Kararriak, bolumen berean urak baino 2,6 aldiz gehiago pisatzen duela esan nahi du horrek. Grabitate-zentrua. Gorputz homogenoak eta heterogenoak Badakigu edozein gorputzi Lurrak bere zentru aldera erakarrita indarra (grabitate-indarra edo pisua) eragiten diola. Grabitate-indarra gorputzaren zati guztietan eragiten da. Grabitate-zentrua, gorputz batean eragiten duten grabitate-indar partzial guztien erresultantearen aplikagunea da. Berunezko lamina karratu bat baldin badugu, adibidez, eta bere bi zati (A eta B) kontsideratzen baditugu (ikus a. irudia), A zatian Lurrak P 1 indarra eragiten du behera eta B zatian P 2 indarra. Bi indar horiek kontsideratzeak edo karratuaren zentruan (grabitate-zentruan) P indarra kontsideratzeak berdin dio, baldin eta P = P 1 + P 2 baldin bada. P indarra da indar erresultantea eta karratuaren zentrua indar erresultantearen aplikagunea. P 1 eta P 2 indarrak berdinak izango dira, baldin A eta B zatiek azalera berdina badute eta A eta B zatiak material berdinaz eginda badaude (bestela esan, karratu osoa material homogenoz egina badago). Besterik litzateke karratuaren A alderdia material batez (berunez, adibidez) eta B alderdia beste batez (paperez, esaterako) eginak baleude, alde bateko eta besteko pisu espezifikoak desberdinak direlako. Karratua material heterogenoz egina dagoela esango dugu kasu horretan. Plazan jasotzeko erabiltzen den granitozko harriak bere barruan, adibidez, beste pisu espezifiko bat duen mineralezko betak baldin baditu, Fisikan material heterogenoa dela esaten da. Material homogenoz egindako gorputz geometrikoen grabitate-zentrua non dagoen jakitea erraza da. Harrizko esfera homogenoaren (hau da, esferako puntu guztietan harriak pisu espezifiko bera duenean) grabitate-zentrua, esferaren zentru geometrikoan dago. Harri kubiko homogenoaren grabitate-zentrua, kuboaren zentru geometrikoan dago. 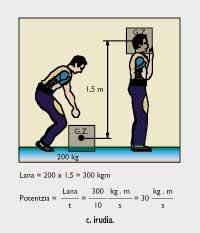Bi material heterogenoz osatutako multzoa dugunean ordea, grabitate-zentrua kalkulatzea konplikatuagoa da. b.1. irudian, pisu espezifiko desberdineko bi gorputz esferiko (A eta B) a distantziara kokatuta daude. A gorputzaren pisua P 1 da eta bere grabitate-zentrua esferaren zentruan du. B gorputzaren pisua berriz, P 2 da eta grabitate-zentrua esferaren zentruan dago. Lurrak pisu espezifiko desberdineko bi esfera horiei eragindako P 1 eta P 2 indarren ordez bi horien Pr indar erresultante bakarra ipinita efektu berbera lortuko dugu. Baina, hori bai, indar erresultanteak beste bien batura izan behar du eta indar erresultantearen aplikaguneak irudian adierazitako G.Z. puntuan egon behar du (grabitate-zentruan, alegia). Aplikagunea A gorputzetik b distantziara dago eta B gorputzetik c distantziara. b eta c distantziak kalkulatzeko formulak irudian bertan erakusten dira. b2. irudian, pisu espezifiko desberdineko hiru pisuren erresultantea (P r ) eta beren grabitate-zentrua (G.Z.) nola kalkulatu erakusten da. Bide batez, pisu gehiagoren erresultantea eta grabitate-zentrua nola lor daitezkeen ere erakusten da. Indarra, lana eta potentzia Pisua gure kasuan, Lurrak harriari beherantz eragiten dion erakarmen-indarra da, eta harrijasotzaileak 100 kilo pisatzen duen harriari erori gabe eutsi nahi badio, gorantz 100 kiloko indarra eragin beharko dio bere grabitate-zentruan. Harriari bere horretan geldirik eusten badio, Fisikaren ikuspegitik harrijasotzaileak ez du lanik egin. Fisikan lana egon dadin, gorputza (harria kasu honetan) indarra eraginda desplazatu egin behar da. Lana berriz, honela definitzen da Fisikan: eragiten den indarra bider gorputzaren desplazamendua. Pentsa dezagun c. irudian harrijasotzaile batek 200 kiloko pisua duen harri kubikoa bizkarrera altxatu behar duela. Harria lurretik bizkar gaineraino altxatu du eta harriaren grabitate-zentrua ere igo egin da. Lurretik bizkar gaineraino harriaren grabitate-zentruak 1,5 metro egin du gora. Kasu horretan Fisikan harrijasotzaileak 200 kg bider 1,5 metro edo 300 kilogrametroko (kg x m-ko) lana egin duela esaten da. Lana beraz, indarra bider distantzia da. Hemen esandakotik erraz ikus daiteke harriak lurrean dagoenean bere grabitate zentrua zenbat eta gorago eduki, harrijasotzaileak bizkarreraino altxatzeko hainbat eta lan gutxiago egin behar duela. Izan ere, bizkarrerainoko distantzia 1,5 metro baino txikiagoa izango litzateke, eta esan dugunez lana pisua (edo indarra) bider distantzia da. Beraz, pisu bera eta distantzia txikiagoa izango luke. Harrijasotzailea mozkotea edo txikia bada ere, abantaila du. Izan ere, harria lurretik bizkarreraino jaso behar du eta bizkarra harrijasotzaile altuak baino beherago duenez, 1,5 metroko distantzia hori txikiagoa litzateke eta egindako lana (indarra edo pisua bider distantzia) ere bai. Guk, egia esan, beste kiroletan ere ikusten ditugu horrelako kasuak. Atletismoan altuera-jauzian adibidez, bi metroko altuera nekez saltatuko du metro t’erdiko gizon edo emakumeak. Harrijasotzean ere berdin gertatzen da: indarrez berdin dauden bi harrijasotzaile parean ipinita, lurretik sorbaldara distantzia txikiena duenak abantaila du. Fisikan potentzia berriz, denbora-unitateko egiten den lana da. c. irudiko harrijasotzaileak 200 kiloko harria hamar segundotan altxatzen badu, 300 kg x m/10 s-ko edo 30 kg x m/s-ko potentzia erabili duela esaten da. Batzuetan potentzia kg x m/s-tan eman ordez watt (W) edo zaldi-potentziatan (ZP) ematen da. Esan dezagun, bada, 1 kg x m/s = 9,807 watt = 1,315 x 10 -2 ZP dela. 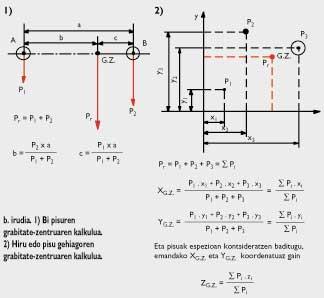Zenbait materialen pisu eskezifiko erlatiboak Kararria = 2,6-2,7 Granitoa = 2,65-2,85 Baritina = 4-4,7 Igeltsoa = 1 (masa egin eta lehortua) Ura = 1 Aluminioa = 2,7 Zinka = 7,14 Eztainu grisa = 7,28 Burdina = 7,88 Kobrea = 8,92 Nikela = 8,92 Zilarra = 10,5 Beruna = 11,34 Merkurioa = 13,55 Urrea = 19,30 Wolframioa = 19,32 Platinoa = 21,45 Iridioa = 22,42 Oharra : Zerrendaren hasieran normalean harrijasotzen edo pisujasotzen erabiltzen diren materialen pisu espezifiko erlatiboak ipini ditugu. Material bati bi zifra ipini dizkiogunean (granitoari 2,65-2,85 adibidez), material horren pisu epezifiko eraltiboa bi zifra horien artekoa izaten dela esan nahi dugu.

Oharra: Artikulu honetako argazkiak ongi ikusteko PDF formatuan daude ikusgai.