Cossos platònics

1998/02/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

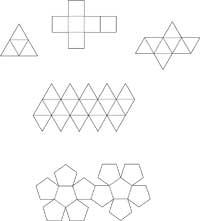
No, aquests cossos forts, esvelts i bruns que veiem al sol o a l'ombra durant les vacances d'estiu. No, tampoc són els que fan culturisme. També està equivocat el que ha pensat en els xais rostits que se serveixen en “Platons”. Els cossos platònics són només poliedres regulars. Als poliedres regulars se'ls ha anomenat també cos còsmic o cos platònic per les formes que Plató aplica en la seva obra Timeo per a explicar científicament els fenòmens. En total són cinc: tetraedre, hexaedre (cub), octaedre, dodecaedre i ikosaedro (figura 1). Les cinc es caracteritzen per estar formades per polígons regulars del mateix tipus i convexos; el tetraedre, octaedre i icosaedre estan formats per triangles equilàters, l'hexaedre quadrat i el dodecaedre en pentàgon.

Nombredelescanterpinactetraedro4 triángulo64Hexaedroa6 cuadratu128Octaedro8 triangulo126 Dodecaedroa12 pentagono3020Ikosaedroaedro20 triangulo 3012

Fórmula d'Euler

Costats + Vèrtexs = Arestes + 2

Plató (a. C.) 427-347) no va suposar en si mateix resultats tècnics per a les matemàtiques. No obstant això, va ser el veritable centre de l'activitat matemàtica de l'època i a més d'influir personalment en el seu desenvolupament, també la va dirigir. A les portes d'accés al col·legi d'Atenes es deia: “Que no entri ningú que no sàpiga geometria”. La seva responsabilitat matemàtica, més que com a matemàtica, la va donar a conèixer com a matemàtica. Sembla que el reconeixement de Plató de les matemàtiques no provenia del seu mestre Sòcrates. Arquitecte, el seu amic, va ser el que es va acostar a les matemàtiques Plató. L'any 300 li va visitar a Sicília. Potser allí va conèixer per primera vegada els cinc cossos regulars citats.

El tetraedre, l'hexaedre, l'octaedre i l'ikosaedro es relacionaven amb els quatre elements d'Enpedokles en un esquema còsmic que ha fascinat a l'home durant segles (Figura 2). D'altra banda, els Pitágoros admiraven al dodecaedre. Plató va reconèixer el dodecaedre, cinquè i últim cos regular, com a símbol de l'univers.

El foc, l'aire, l'aigua i el sòl s'uneixen amb el tetraedre, l'octaedre, l'ikosaedro i l'hexaedre respectivament. A excepció dels de l'hexaedre, atès que els costats dels altres poliedres són triangles equilàters i, per tant, similars, els elements corresponents, foc, aire i aigua, podrien tornar-se mutus, però no terres, ja que les cares de l'hexaedre són quadrades. Els quadrats no es poden descompondre en triangles equilàters, només es poden descompondre en triangles rectilinis isòsceles. D'altra banda, el poliedre de menor volum respecte a la seva superfície és el tetraedre, d'on sembla desprendre's la unió al foc. El més voluminós en superfície és l'ikosaedro, per la qual cosa s'ha unit a l'aigua. L'hexaedre, per part seva, és estable respecte a la seva base, per la qual cosa s'ha unit al terreny. En girar l'octaedre agarrat per dos vèrtexs oposats, s'ha adequat a l'aire que es mou. El poliedre regular cinquè, dodecaedre, està format per pentàgons i els pentàgons tampoc poden descompondre's en triangles equilàters, i el dodecaedre té 12 costats, reflex dels 12 signes del zodíac, d'aquí la seva relació amb l'univers.

En Timeo, on porta el nom del seu interlocutor principal, va exposar les seves idees sobre els cossos regulars platònics. No sabem si el de Timeo Lokia va existir realment o ho va inventar Plató amb l'excusa d'explicar les seves idees pitagòriques.

Plató va escriure aquest col·loqui als 70 anys, en el qual ens dóna la primera petjada exacta de la relació entre els quatre elements i els cossos regulars, però molts dels episodis d'aquesta fantasia es deuen als pitagòrics. Segons Proklo, Pitàgores va construir la imatge còsmica, però l'escolàstic Suidas deia que Teeteto (amic de Plató, a. C.). Nascut l'any 414, va ser el primer que va escriure sobre aquest tema.

Euklides va dedicar l'últim llibre de “Elements”, el xiii, als poliedres regulars. En ell ens va donar relacions entre les vores dels poliedres i els radis de les esferes inscrites i circumscrites. Finalment, com a lema apareixia el teorema que es va afegir més tard: a més dels cinc poliedres regulars coneguts, no hi ha un altre poliedre regular.

XIII Elements d'Euklides. segons un col·legi de data desconeguda del llibre, els pitagòrics només coneixien tres cossos regulars i l'octaedre i l'icosaedre van ser coneguts per Teeteto. No obstant això, sembla que Teeteto va realitzar un de les anàlisis sistemàtiques llavors dels poliedres regulars i ell mateix va escriure el teorema que hi ha cinc i només cinc poliedres regulars. Apika, en l'últim llibre de “Elements”, també són seus els càlculs de les causes entre les vores dels cossos regulars i el radi de l'esfera circumscrita.

Tant en aritmètica com en geometria, Plató es va posicionar a favor de la matemàtica pura, enfront de les concepcions materialistes de l'artesà i tècnic. Plutarko va recollir en la seva obra “La vida de Marcelo” l'empipament de Plató davant l'ús d'artificis mecànics en la geometria; Plató considerava aquest ús com la corrupció i la simple cancel·lació del bé existent en la geometria, donant la seva esquena descaradament a objectes sense cos de pura intel·ligència. En conseqüència, Plató va poder ser, en gran manera, responsable de la principal restricció a les construccions de geometria que només es poden realitzar mitjançant compàs i regla. La raó d'aquesta reducció no va anar probablement la simplicitat dels instruments utilitzats, sinó la simetria dels construïts: qualsevol diàmetre del cercle és l'eix de simetria; qualsevol punt de la recta és el centre de simetria; qualsevol unió amb una recta és el seu eix de simetria.

La filosofia platònica, divinitzant les idees, havia de posar en primer lloc la recta i la circumferència entre totes les figures geomètriques. De manera similar, Plató va enaltir el triangle. Per a Plató, les diferències dels cinc poliedres regulars no eren mers triangles, quadrats i pentàgons. Per exemple, cada costat del tetraedre estava format per sis triangles rectilinis menors (obtinguts per altures), descomponent-se el tetraedre en 24 triangles rectes escalens. Així mateix, octaedre i icosaedre en 48 i 120 triangles rectilinis escalens, respectivament, i hexaedre en 24 triangles rectes isòsceles.

Plató va donar un paper especial al dodecaedre, com a representant de l'univers, dient que “Déu el va utilitzar íntegrament” (Timeo, 55). Plató considerava el dodecaedre com un conjunt de 360 triangles rectilinis escalens, ja que dibuixant en els pentàgons les cinc diagonals i les intermèdies queden 30 triangles.

En unir els quatre primers poliedres regulars amb els quatre elements de l'univers, Timeon va donar una bonica teoria unificada de la matèria, segons la qual tot està format per triangles rectilinis ideals i la fisiologia, en el seu conjunt, igual que la ciència de la matèria inerta, està basada en el funcionament d'aquests triangles. El creixement del cos d'un animal, per exemple, el va explicar:

“La Constitució de la Criatura, íntegrament, quan encara és jove i els seus components són de recent construcció, les seves puntes estan fortament interrelacionades… Qualsevol dels triangles que componen els aliments i begudes…, més antic i més feble que els seus, ho tallen els seus triangles recentment fetes i per això treu el millor profit i això és el que fa créixer a l'animal.En la
vellesa, per contra, els triangles que formen el cos estan tranquils pel seu ús i no poden tallar els triangles de l'aliment que ingereixen, mentre que les sarquinas que vénen de l'exterior parteixen amb facilitat les seves i la criatura s'esgota i cau.”